II Закрепление изученного материала

Соотношения между тригонометрическими функциями

Одного и того же аргумента. Применение основных тригонометрических формул к преобразованию выражений.

Цели:

- научиться находить соотношения между тригонометрическими функциями;

- повторить уравнение окружности;

- формировать умения и навыки использования тригонометрических тождеств при решении задач.

Ход урока

I Изучение нового материала

Пусть при повороте начального радиуса ОА, равного R, на угол . Тогда по определению =  , где x – абсцисса точки В, а y – ордината. Отсюда следует, что   Тогда В принадлежит окружности. Поэтому ее координаты удовлетворяют уравнению:

.

Воспользуемся равенствами:  получим:

Отсюда:

    (1)

Формула (1) выражает соотношение между синусом и косинусом одного аргумента.

Выясним теперь как связаны между собой тангенс и котангенс одного и того же аргумента. По определению

tg . Т.к.  то  

tg =    (2)

ctg     (3).

Равенство (1) верно при любых значениях . Равенство (2) верно при всех значениях , при которых , а равенство (3) верно при всех значениях , при которых .

С помощью этих формул можно получить другие формулы, выражающие соотношения между тригонометрическими функциями одного и того же аргумента. Из равенств (2) и (3) получаем:

    tg , т.е.

tg  1. (4)

Равенство (4) показывает, как связаны между собой тангенс и котангенс одного аргумента. Оно верно при всех значениях , при которых tg  имеют смысл.

Выведем теперь формулы, выражающие соотношения между тангенсом и косинусом, а также между котангенсом и синусом одного и того же аргумента.

Разделив обе части равенства (1) на  получим:

    

. (5)

 

Если обе части равенства (1) разделить на 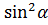, то

              

. (6)

Равенство (5) верно, когда , а равенство (6) – когда .

 

Равенства (1) – (6) являются тождествами. Их называют основными тригонометрическими тождествами.

Формулы двойного аргумента

                  

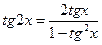
II Закрепление изученного материала

Пример 1. Известно, что . Найти .

Решение. Из формулы (1) получаем: . Подставив заданное значение синуса, получим

.

Значит либо . По условию, , т.е. аргумент принадлежит III четверти. В III четверти косинус отрицателен, значит

.

Ответ: -0,8.

Пример 2. Упростить выражение .

.

Пример 3. Упростить выражение

Пример 4. Упростить выражение

2) cos²α – (ctg²α +1) sin²α.=

Пример 5. Докажите тождество:

1) (tg α+ctg α)²– (tg α–ctg α)²= 4

Тождество доказано.

2) (1+tg α)²+(1-tg α)²= ;

Тождество доказано.

Пример 6.  Упростите выражение .

Пример 7.  Упростите выражение .

.

 

 

Домашнее задание: Колмогоров А.Н. Алгебра 10-11. § 1, пункт 2 (стр. 7-9).