Определяем знак результата

Алгебра 10 класс

Урок № 2 (03.04.2020 г.)

Тема: «Самостоятельная работа. Формулы приведения»

Задания

Решить самостоятельную работу.

Номер варианта – сумма букв фамилии и имени.

Каждый правильно решенный пример оценивается в 1б.

ВАРИАНТ 1	ВАРИАНТ 2	ВАРИАНТ 3	ВАРИАНТ 4
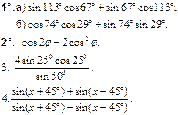
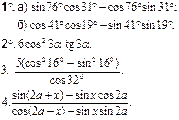
ВАРИАНТ 5	ВАРИАНТ 6	ВАРИАНТ 7	ВАРИАНТ 8
ВАРИАНТ 9	ВАРИАНТ 10	ВАРИАНТ 11	ВАРИАНТ 12
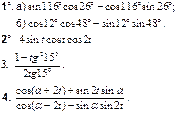
ВАРИАНТ 13	ВАРИАНТ 14	ВАРИАНТ 15	ВАРИАНТ 16
ВАРИАНТ 17	ВАРИАНТ 18	ВАРИАНТ 19	ВАРИАНТ 20

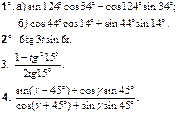
Теория

ФОРМУЛЫ ПРИВЕДЕНИЯ

Формулы приведения применяются к выражениям вида sin(); cos(); tg(360⁰ + α) и т.д. Углы  расположены на осях координат и 0<α<90⁰.

       Для записи формул приведения руководствуются следующими правилами:

 1) определяем, менять функцию на кофункцию или нет (то есть sinα на cosα, а cosα на sinα; tgα на сtgα, сtgα на tgα)

Если есть  и т.д. (углы находятся на оси у), то функцию меняем на кофункцию.

Если есть p, 2p, 3p и т.д. (углы находятся на оси х), то функцию НЕ меняем на кофункцию.

определяем знак результата

Выясняем, в какой четверти находится аргумент изначальной функции, определяем знак и ставим его перед результатом.

Эти правила изображены на слайдах:

Примеры. Преобразовать тригонометрические выражения:

a) sin( )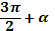

1)  находится на вертикальной оси (на оси у) Þ меняем на кофункцию, то есть синус меняем на косинус Þ вместо выражения sin() записываем cosα.         

   убираем! α оставляем всегда со знаком «+»

2) (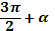) находится в 4й четверти, в ней синус имеет знак «–» Þ перед результатом ставим знак «–», то есть sin( 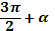) = – cosα.

 

b) tg(p + α)

1) p находится на горизонтальной оси (на оси х) Þ не меняем на кофункцию Þ вместо выражения tg(p + α) записываем tgα.

  p убираем! α оставляем со знаком «+»

2) (p + α) находится в 3й четверти, в ней тангенс имеет знак «+» Þ перед результатом ставим знак «+», то есть tg(p + α)= tgα.

 

c) cos( )

1) находится на вертикальной оси (на оси у) Þ меняем на кофункцию, то есть косинус меняем на синус Þ вместо выражения cos() записываем sin2α.    

   убираем! 2α оставляем со знаком «+»

2) () находится в 1й четверти, в ней косинус имеет знак «+» Þ перед результатом ставим знак «+», то есть cos( ) = sin2α.

d) ctg(α – 90⁰)

Данное выражение можно преобразовать двумя способами: ctg(α – 90⁰) = ctg(– 90⁰ + α) или ctg(α – 90⁰) = – ctg(90⁰ – α), а затем воспользоваться выше описанными правилами.

Получим: ctg(α – 90⁰) = – tgα.

e) Вычислить sin210⁰

sin210⁰ = sin(180⁰ + 30⁰) = – sin30⁰ = – .

f) Вычислить cos( )

cos(  ) = cos(  ) = cos  = .

g) Вычислить sin78⁰cos18⁰ – sin18⁰sin12⁰

Приведем выражение к формуле cos(α + β):

sin78⁰ = sin(90⁰ – 12⁰) = cos12⁰ Þ

sin78⁰cos18⁰ – sin18⁰sin12⁰ = cos12⁰cos18⁰ – sin18⁰sin12⁰ = cos(12⁰ + 18⁰) = cos30⁰ = .

Проверить правильность применения формул приведения можно по таблице:

 

Задания

1) Прочитать: § 31

2) Записать в тетради для теории правила применения формул приведения 

3) Посмотреть видеоуроки:

Формулы приведения теория:

https://www.youtube.com/watch?v=DHA8oPjlzAw

https://www.youtube.com/watch?v=K0b8fhEgBek

Примеры решения:

https://www.youtube.com/watch?v=j-ofo5K2fm4

https://www.youtube.com/watch?v=-0kA_JYNcxg&list=PLBnDGoKqP7bbXfM7jrSQzkTEkFJdF4YxP&index=16&t=0s