Урок 9 Вычисления. Действия с дробями

Алгебра 9 класс

Урок 7 - 9

Урок 7

Чтение графиков функций

Задание 11

Найдите значение по графику функции , изображенному на рисунке.

 

1)

2)

3)

4)

Решение.

Абсцисса вершины параболы равна −1, поэтому откуда Парабола пересекает ось ординат в точке с ординатой 3, поэтому 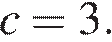Тем самым, уравнение параболы принимает вид Поскольку парабола проходит через точку (−1; 2), имеем:

 

 

Верный ответ указан под номером 2.

 

Ответ: 2.

Ответ: 2

193089

2

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

Найдите значение по графику функции , изображенному на рисунке.

 

1)

2)

3)

4)

Решение.

Абсцисса вершины параболы равна −1, поэтому откуда 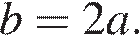Парабола пересекает ось ординат в точке с ординатой 3, поэтому 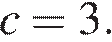Тем самым, уравнение параболы принимает вид Поскольку парабола проходит через точку (−1; 2), имеем:

 

 

Таким образом,

 

Верный ответ указан под номером 3.

 

Ответ: 3.

Ответ: 3

193090

3

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

Найдите значение по графику функции изображенному на рисунке.

1)

2)

3)

4)

Решение.

Значение — это значение графика при ордината графика при Значит, 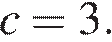Такой ответ указан под номером 4.

 

Ответ: 4.

Ответ: 4

193091

4

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

Найдите значение по графику функции изображенному на рисунке.

Решение.

Поскольку гипербола проходит через точку (−1; 1), имеем:

 

Ответ: −1.

Ответ: -1

193102

-1

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

 

1) функция возрастает на промежутке

2)

3)

4) прямая пересекает график в точках и

Урок 8

Чтение графиков функций

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и 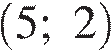— верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

 

Ответ: 12.

Ответ: 12|21

311406

12|21

Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

На рисунке изображён график квадратичной функции y = f (x).

Какие из следующих утверждений о данной функции неверны? Запишите их номера в порядке возрастания.

 

1) Функция возрастает на промежутке (−∞;  −1].

2) Наибольшее значение функции равно 8.

3) f (−4) ≠ f (2).

Решение.

Проверим каждое утверждение.

1) На луче (−∞;  −1] большему значению аргумента сответствует большее значение функции. Следовательно, функция возрастает на этом луче; первое утверждение верно.

2) Наибольшее значение функции равно 9. Второе утверждение неверно.

3) Значения фунцкии в точках −4 и 2 равны нулю, поэтому f (−4) = f (2). Третье утверждение неверно.

 

Ответ: 23.

Ответ: 23

314676

23

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

На рисунке изображён график квадратичной функции y = .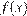

Какие из следующих утверждений о данной функции неверны? Запишите их номера.

 

1) =

2) Наибольшее значение функции равно 3.

3) 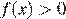при

Решение.

Проверим каждое утверждение.

1) = 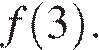Первое утверждение верно.

2) Наибольшее значение функции равно 4. Второе утверждение неверно.

3) при 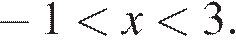Третье утверждение верно.

 

Ответ: 2.

Ответ: 2

314703

2

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

На рисунке изображён график квадратичной функции y = f(x).

Какие из следующих утверждений о данной функции неверны? Запишите их номера.

 

1) Наибольшее значение функции равно 9.

2) f (0)> f (1).

3) f(x) >0 при x <0.

Решение.

Проверим каждое утверждение.

 

1) Наибольшее значение функции равно 9. Первое утверждение верно.

2) Значения фунцкии в точке 0 равно 8, а в точке 1 — 5 поэтому f (0) > f (1). Второе утверждение верно.

3) На луче (−∞;  0) функция принимает как положительные так и отрицательные значения. Третье утверждение неверно.

 

Ответ: 3.

Ответ: 3

314704

3

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

На рисунке изображён график функции y = ax² + bx + c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

 

 

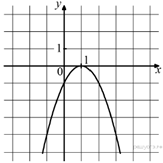
УТВЕРЖДЕНИЯ		ПРОМЕЖУТКИ
А) функция возрастает на промежутке Б) функция убывает на промежутке		1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3]

 

Ответ:

Решение.

Функция, изображённая на графике возрастает на промежутке и убывает на промежутке Следовательно, на данных промежутках функция возрастает на третьем промежутке и убывает на первом.

 

Ответ: 31.

Ответ: 31

333008

31

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

На рисунке изображён график функции вида 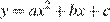. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

 

УТВЕРЖДЕНИЯ		ПРОМЕЖУТКИ
А) функция возрастает на промежутке Б) функция убывает на промежутке		1) [0; 3] 2) [−1; 1] 3) [2; 4] 4) [1; 4]

 

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А	Б

Решение.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Данная функция возрастает на промежутке и убывает на промежутке Таким образом, из приведённых промежутков функция только возрастает на промежутке убывает на промежутке

 

Ответ: 23.

Ответ: 23

333087

23

Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.

Задание 11

На рисунке изображены графики функций вида y = ax ² + bx + c. Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D.

 

Графики

А)

Б)

В)

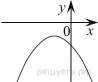
Г)

Знаки чисел

 

1) a > 0,  D > 0

2) a > 0,  D < 0

3) a < 0,  D > 0

4) a < 0,  D < 0

 

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А	Б	В	Г

 

Урок 9 Вычисления. Действия с дробями

 Решите примеры:

1. Найдите значение выражения:

Решение.

Выполним преобразования:

 

Ответ: −500.

Ответ: -500

16621

-500

Раздел кодификатора ФИПИ: Действия с дробями

2. Найдите значение выражения .

Решение.

Выполним преобразования:

 

.

Ответ: 80,625.

Ответ: 80,625

26900

80,625

Раздел кодификатора ФИПИ: Действия с дробями

3. Найдите значение выражения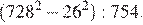

Решение.

Выполним преобразования:

.

Ответ: 702.

Ответ: 702

86983

702

Раздел кодификатора ФИПИ: Действия с дробями

4. Найдите значение выражения

Решение.

Представим в дроби в десятичном виде и выполним сложение:

 

Ответ: 2,65.

Ответ: 2,65

506120

2,65

Источник: Де­мон­стра­ци­он­ная версия ЕГЭ—2015 по математике. Базовый уровень. Вариант 1.

Раздел кодификатора ФИПИ: Действия с дробями

5. Найдите значения выражения:

Решение.

Найдём значения выражения:

 

 

Ответ: 0,4.

Ответ: 0,4

507521

0,4

Раздел кодификатора ФИПИ: Действия с дробями

6. Найдите значение выражения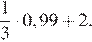

Решение.

Найдём значение выражения:

 

 

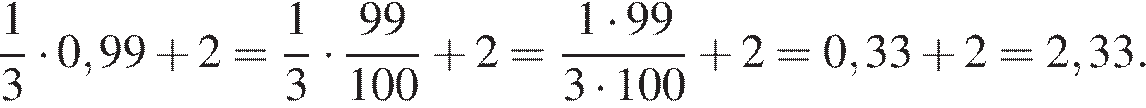
Ответ: 2,33.

Ответ: 2,33

509208

2,33

Источник: ЕГЭ по ба­зо­вой математике 26.03.2015. До­сроч­ная волна

Раздел кодификатора ФИПИ: Действия с дробями

7. Найдите значение выражения (3,9 − 2,4) · 8,2.

Решение.

Найдём значение выражения:

 

 

Ответ: 12,3

509586

12,3

Раздел кодификатора ФИПИ: Действия с дробями

8. Найдите значение выражения

Решение.

Найдём значение выражения:

 

 

Ответ: 4.

Ответ: 4

509606

4

Раздел кодификатора ФИПИ: Действия с дробями

9. Найдите значение выражения

Решение.

Найдём значение выражения:

 

 

Ответ: -1,3.

Ответ: -1,3

509626

-1,3

Раздел кодификатора ФИПИ: Действия с дробями

10. Найдите значение выражения

Решение.

Найдём значение выражения:

 

 

Ответ: 8.

Ответ: 8

509646

8

Раздел кодификатора ФИПИ: Действия с дробями

11. Найдите значение выражения 3,8 + 1,08: 0,9.

Решение.

Найдём значение выражения:

 

 

Ответ: 5.

Ответ: 5

509706

5

Раздел кодификатора ФИПИ: Действия с дробями

12. Найдите значение выражения

Решение.

Найдём значение выражения:

 

 

Ответ: 5.

Ответ: 5

509726

5

Раздел кодификатора ФИПИ: Действия с дробями

13. Найдите значение выражения

Решение.

Найдём значение выражения:

 

 

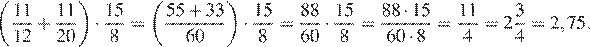
Ответ: 2,75.

Ответ: 2,75

509766

2,75

Раздел кодификатора ФИПИ: Действия с дробями

14. Найдите значение выражения

Решение.

Найдём значение выражения:

 

 

Ответ: 24,7.

Ответ: 24,7

510017

24,7

Раздел кодификатора ФИПИ: Действия с дробями

15. Найдите значение выражения

Решение.

Последовательно получаем:

 

 

Ответ: 1,8

Ответ: 1,8

510192

1,8

Раздел кодификатора ФИПИ: Действия с дробями