Примеры решения задач

Семинар 4. Магнитные свойства атомов

План занятия

1. Краткое теоретическое введение

2. Разбор типовых задач (Л-3: 5.206, 5.210, 5.215)

3. Самостоятельное решение задач (5.205, 5.211, 5.220)

Теоретическая часть

Для состояний, принадлежащих данному L, S, J -мультиплету (), оператор магнитного момента атома можно представить в виде

, (1)

где

(2)

называют g –фактором или фактором (множителем) Ланде, L, S, J – квантовые числа, определяющие мультиплет , 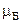‑ магнетон Бора.

Минимальное значение фактора Ланде (2) равно нулю. В этом случае магнитный момент атома тоже равен нулю, хотя его момент импульса может быть отличен от нуля. Если орбитальный момент импульса атома равен нулю (L = 0), полный момент импульса атома совпадает со спиновым моментом (J = S). Подстановка в (11) L = 0 и J = S дает g = 2 (это является результатом того, что для спина коэффициент пропорциональности между магнитным моментом и моментами импульса равен ). Для атомов, у которых спиновый момент импульса равен нулю (S = 0) полный момент импульса совпадает с орбитальным J = L, что с очевидностью приводит к g = 1.

Таким образом, магнитный момент многоэлектронного атома равен:

Атом в магнитном поле. Эффект Зеемана

Взаимодействие магнитного момента атома с магнитным полем приводит к приобретению атомом дополнительной энергии, оператор которой имеет вид

, (3)

где 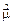- оператор магнитного момента атома (1).

Направим ось вдоль вектора при этом (3) примет вид

. (4)

Собственными значениями оператора являются магнитные квантовые числа ().

Поэтому уровни энергии атома в магнитном поле:

(5)

Выражение (5) говорит о том, что при наложении магнитного поля состояние атома с полным моментом импульса, определяемым квантовым числом J, расщепляется на 2 J +1 - состояния - происходит снятие выражения уровней мультиплета по магнитному квантовому числу.

Примеры решения задач

Задача 5.206. Найти полный механический момент атома в состоянии с и , если известно, что магнитный момент его равен нулю.

Решение: Магнитный момент атома , где - фактор Ланде, может быть равен нулю при 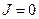, либо в случае .

Квантовое число при и может иметь значения , ни одно из которых не равно нулю. Поэтому в нашем случае фактор Ланде, определяемый соотношением , должен быть равен нулю. Откуда следует: .

Подставим в это соотношение численные значения и и найдем . Решив это уравнение для J получим: , которое является одним из возможных значений . Таким образом полный механический момент атома .

Задача 5.210. Узкий пучок атомов серебра в основном состоянии пропускают по методу Штерна и Герлаха через поперечное неоднородное магнитное поле В, сосредоточенное в области l₁ = 5 см. Расщепление пучка наблюдают на экране, отстоящем от магнита на расстоянии l₂ = 15 см. Кинетическая энергия атомов Т = 22 мэВ. При каком значении градиента индукции магнитного поля величина между крайними компонентами расщепленного пучка составляет d = 2 мм?

Решение: Атом серебра в состоянии ( L = 0, g = 2) обладает магнитным моментом Энергия атома в магнитном поле где магнитное квантовое число m_J может принимать значения – J, – J +1, …, + J.

В неоднородном магнитном поле на атом будет действовать сила в поперечном направлении (ось z направлена вертикально вверх) под действием которой атомы и будут отклоняться. По условию нам известно максимальное отклонение пучка атомов, оно соответствует максимальному значению силы, реализующемуся при m_J = – J. На рисунке показана схема опыта Штерна и Герлаха. Максимальное смещение пучка где z ₁ – смещение при движении атома между полюсами магнита; z ₂ – смещение при движении от края магнита до экрана. В магнитном поле атом серебра движется
с ускорением где m – масса атома серебра; его движение в поле продолжается в течение времени Поэтому

За это время атом приобретет составляющую скорости

Поэтому

Расстояние между крайними компонентами расщепленного пучка

Откуда

Задача 5.215. Известно, что спектральная линия 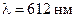обусловлена переходом между синглетными термами атома. Вычислить интервал между крайними компонентами этой линии в магнитном поле с индукцией .

Решение: Расщепление уровней энергии мультиплета в магнитном поле определяется выражением , где - фактор Ланде, 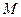- магнитное квантовое число. У синглетных термов . Поэтому для них и фактор Ланде .

Запишем уровни энергии возбужденного (индекс 2) и основного (1) термов в магнитном поле

, .

Частоты излучения

, (1)

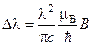где . Согласно правилам отбора . При этом (1) можно представить в виде , где . Поскольку , то . Расстояние между крайними компонентами (), откуда следует . Подставим численные значения величин и найдем .