Практическое занятие 8

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятности появления этих событий без вероятности их совместного появления

 

P (A + B) = P (A) + P (B) - P (A×B)

 

Пример. Рабочий обслуживает два станка. Вероятность того, что в течении часа первый станок будет работать без сбоя равна 0.9; для второго станка эта вероятность равна 0.8. Какова вероятность, что без сбоя будет работать хотя бы один станок?

Решение. Первый способ. Пусть A _1, A ₂ события, состоящие в том, что соответственно первый и второй станок будут работать без сбоя. Тогда вероятность того, что без сбоя будет работать хотя бы один станок, равна вероятности суммы этих событий; по формуле получим

 

.

 

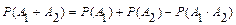Значит,

.

 

Второй способ. Пусть событие  - без сбоя будет работать хотя бы один из двух станков. Найдём вероятность этого события с помощью вероятности противоположного события  (оба станка будут работать со сбоями). Тогда,

 

 

Третий способ. Представим сложное событие A = A ₁ + A ₂ в виде суммы трёх несовместных событий .

Тогда,

 

P (A) = 0,9×0,2 + 0,1×0,8 + 0,9×0,8 = 0,18 + 0,08 + 0,72 = 0,98.

 

Ответ: 0,98.

 

Система событий А ₁, А ₂,..., А_n называется независимой в совокупности, если вероятность произведения равна произведению вероятностей для любой комбинации сомножителей из этой системы.

Формулы полной вероятности и Байеса. Пусть события
Н ₁, Н ₂,..., Н_n попарно несовместны и в сумме образуют достоверное событие (в этом случае их называют гипотезами). Эти события образуют полную группу событий. Пусть теперь интересующее нас событие А наступает после реализации одной из гипотез Н_i и известны вероятности , . В этом случае вероятность события А вычисляется по формуле полной вероятности       

Если дополнительно стало известно, что событие А произошло, то по формуле Байеса можно определить вероятность того, что при этом была реализована Н_k гипотеза (эту вероятность гипотезы, полученную после проведения опыта, называют апостериорной)

Пример. 30% пациентов, поступивших в больницу, принадлежат к первой социальной группе, 20% - второй и 50% - третьей. Вероятность заболевания туберкулёзом для представителей этих групп соответственно равны 0,02, 0,03 и 0,01. Определить вероятность того, что поступивший больной болен туберкулёзом. Проведенные анализы у поступившего больного показали наличие туберкулёза. Найти вероятность того, что это представитель третьей группы.

Решение. Пусть Н ₁, Н ₂, Н ₃ - гипотезы, заключающиеся в том, что пациент принадлежит соответственно первой, второй и третьей группам. Очевидно, они образуют полную группу событий, причём   P(H₁)=0,3, P(H₂)=0,2, P(H₃)=0,5. Вероятность того, что пациент болен определяем по формуле полной вероятности

Вероятность того, что поступивший и оказавшийся больным пациент принадлежит третьей группе определяется формулой Байеса

 

Пример. В цехе работает три типа станков с одинаковой производительностью. Данные о станках приведены в следующей таблице:

 

Тип станка	Количество станков	Доля деталей отличного качества, произведенных на станке
1	5	0,94
2	3	0,9
3	2	0,85

 

Произведенные детали лежат на складе не рассортированными. Определить вероятность того, что взятая случайным образом деталь окажется деталью отличного качества.

Решение. Обозначим события - гипотезы:

H _1, H _2, H ₃ - (взятая деталь изготовлена соответственно на первом, втором и третьем станке);

A - взятая деталь отличного качества.

По условию

 

P (H ₁) = 5/10 = 0,5; P (A | H ₁) = 0,94.

 

P (H ₂) = 3/10 = 0,3; P (A | H ₂) = 0,9.

 

P (H ₃) = 2/10 = 0,2; P (A | H ₃) = 0,85.

 

По формуле полной вероятности

 

P (A) = P (H ₁)× P (A | H ₁) + P (H ₂)× P (A | H ₂) + P (H ₃)× P (A | H ₃)

 

Получим

P (A) = 0,5×0,94 + 0,3×0,9 + 0,2×0,85 = 0,91.

 

Ответ: 0,91.

 

Пример. В трех одинаковых ящиках находятся однотипные детали, среди которых имеются бракованные. Данные о деталях приведены в следующей таблице:

 

Номер ящика	Кол-во деталей	Количество бракованных деталей
1	10	3
2	15	5
3	20	6

 

Взятая наудачу деталь оказалась бракованной. Какова вероятность того, что взятая деталь принадлежала второму ящику?

Решение: Обозначим события:

А – выбранная деталь бракованная;

H_1, H_2, H₃ - (гипотезы) деталь принадлежит соответственно первому, второму, третьему ящику.

 

Тогда, по условию

P (H ₁) = P (H ₂) = P (H ₃) = 1/3.

 

Кроме того, имеем также:

 

P (A | H ₁) = 3/10; P (A | H ₂) = 5/15;         P (A | H ₃) = 6/20.

 

По формуле Байеса,

P (H ₂| A) = .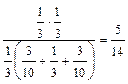

Ответ: 5/14.

Задачи на дом.

 

№1. Определить вероятность угадать три числа в игре «Спортлото – пять из тридцати шести».

 

№2. Определить вероятность прохождения сигнала по электрической цепи за данный промежуток времени, если вероятность безотказной работы элементов А , А , А , А  за это время соответственно равна 0,6; 0,7; 0,8 и 0,8.

 

№3. Рассматриваются всевозможные пятизначные числа. Определить вероятность того, что все цифры случайно выбранного пятизначного числа различны.

 

№4. Определить вероятность прохождения сигнала по электрической цепи за данный промежуток времени, если вероятность безотказной работы элементов А , А , А , А  за это время соответственно равна 0,6; 0,7;0,8 и 0,9.

 

Гмурман № 82, 83, 92 – 94, 98, 101, 102.