Практическое занятие 91

«КОРНИ УРАВНЕНИЙ»

Образец решения:

Пример 1

Уравнения - равносильны?

Решение:

Пример 2

Проверить на равносильность уравнения: .

Решение:

Ответ: равносильны, так как они не имеют корней.

Пример 3

Определить уравнение-следствие при решении уравнений   и

Решение:

 Уравнение  имеет корень 5, уравнение  имеет корни  Так как корень уравнения является корнем уравнения , то уравнение  является следствием уравнения .

Пример 4

Решить двумя способами уравнения и сделать вывод:

а) =

б)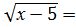

Решение:

а) первый способ:

ОДЗ:

        

        

(  = (, 

,

Оба корня принадлежат ОДЗ уравнения, но это не меняет сути дела и мы вынуждены выполнить проверку корней.

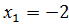Проверка: при  получим  - неверное равенство,  - посторонний корень;

              при , получим  или  - верное равенство, 5 - корень исходного уравнения.

 

Ответ: 5

второй способ:

Исходное уравнение равносильно системе:

            

Решение системы исходного уравнения

Ответ: 5

б) первый способ:

ОДЗ:

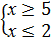
                                                                                           Решений нет

Значит, ОДЗ уравнения пустое множество, уравнение решений не имеет

Ответ: корней нет

второй способ:

Исходное уравнение равносильно системе:

Системы решений не имеют, значит, и исходное уравнение тоже решений не имеет

Ответ: корней нет.

 

Вывод: При решении иррациональных уравнений – возведение обеих частей уравнения в четную степень, принадлежность полученных корней ОДЗ уравнения не позволяет сделать вывод, о том являются ли эти корни посторонними или нет. Поэтому выполнение проверки корней обязательно и это этап решения уравнения. Если корень не принадлежит ОДЗ, то он, конечно, посторонний корень уравнения. В то же время, записывая систему равносильную уравнению, мы не нарушаем логики решения: ведь уравнение с пустой ОДЗ равносильно системе, не имеющей решений.

 

Пример 5

Решить уравнение:

ОДЗ:

 

Решение: Данное уравнение равносильно системам, на основании определения

 

 модуля:

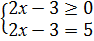       и      

 

 

                           

 

 

 

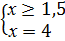
Ответ: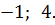

 

Пример 6

Являются ли уравнения равносильными: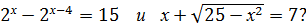

 

Решение:

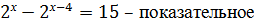уравнение По свойству степеней:  – корень уравнения	– иррациональное уравнение ОДЗ:                                           Данное уравнение равносильно системе:          корни уравнения, так как принадлежат ОДЗ, т.е. геометрически:

 

 

Ответ: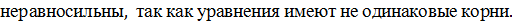

 

Выполнить задания.

1. Добавьте дополнительное условие так, чтобы уравнения: были равносильны   2. Решить 2-мя способами уравнение: и сделать вывод   3. Равносильны ли уравнения:   4. Решить уравнение:  и вычислить полученный результат при 5. Найти корень уравнения:

 

1. Критерии оценивания:

Оценка	Обоснование оценивания
«Отлично»	Все задания выполнены правильно
«Хорошо»	Правильно выполнены любые 4 задания
«Удовлетворительно»	Правильно выполнены любые 3 задания
«Неудовлетворительно»	Правильно выполнено менее 3 заданий