Задание по МАТЕМАТИКЕ
для групп 1-го курса:
ДИН, 0902ДИН,0905КМ, 0906КМ, 0908БАН,
ЛОГ, 0913ЛОГ
Преподаватель: Лобасова Т.А.
Изучить данный теоретический материал, разобрать приведенные в нем примеры с решениями и решить тестовые задания по теме «Тригонометрические функции»
Формулы приведения тригонометрических функций
Формулы, с помощью которых тригонометрические функции произвольного аргумента можно привести к функциям острого угла, называются формулами приведения тригонометрических функций, их можно получить, используя формулы сложения и вычитания аргументов.
Формулы приведения.
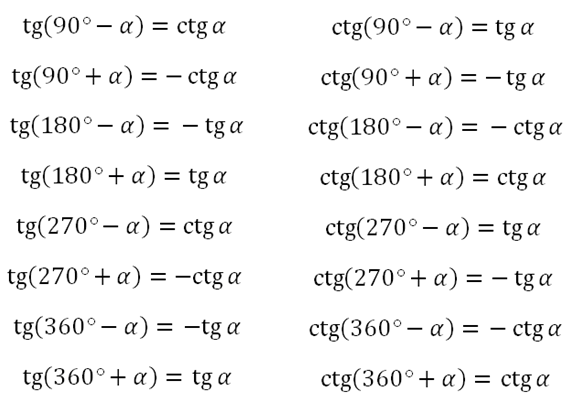


Пример.
Используя формулы приведения, представьте  через синус, а также через косинус острого угла.
через синус, а также через косинус острого угла.
Решение.
Чтобы применить формулы приведения, нам нужно угол 197 градусов представить в виде или 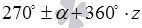 , причем по условию задачи угол должен быть острым. Это можно сделать двумя способами:
, причем по условию задачи угол должен быть острым. Это можно сделать двумя способами:  или
или  . Таким образом,
. Таким образом,  или
или  .
.
Обратившись к соответствующим формулам приведения  и
и  , получаем
, получаем 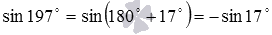 и
и  .
.
Ответ:
 и
и 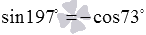 .
.
а) sin 110° = sin (90°+ 20°) = cos 20° ≈ 0,9397
или sin 110° = sin (180° - 70°) = sin 70°≈ 0,9397
б) cos 200° = cos (180° + 20°) = - cos 20°≈ - 0,9397
или cos 200° = cos (270° - 70°) = - sin 70° ≈ - 0,9397
cos 120° = cos (90° + 30°) = - sin 30° = - 1/2
sin 120° = sin (90° + 30°) = cos 30° = 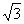 /2
/2
tg 120° = tg (90° + 30°) = - ctg 30° = - 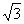
или
- cos 120° = cos (180° - 60°) = - cos 60° = - 1/2
- sin 120° = sin (180° - 60°) = sin 60° =
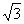 /2
/2 - tg 120° = tg (180° - 60°) = - tg 60° = -
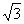
- cos 135° = cos (90° + 45°) = - sin 45° = -
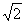 /2
/2 - sin 135° = sin (90° + 45°) = cos 45° =
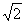 /2
/2 - tg 135° = tg (90° + 45°) = - ctg 45° = - 1
или
- cos 135° = cos (180° - 45°) = - cos 45° = -
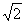 /2
/2 - sin 135° = sin (180° - 45°) = sin 45° =
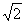 /2
/2 - tg 135° = tg (180° - 45°) = - tg 45° = - 1
- cos 150° = cos (90° + 60°) = - sin 60° = -
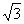 /2
/2 - sin 150° = sin (90° + 60°) = cos 60° = 1/2
- tg 150° = tg (90° + 60°) = - ctg 60° = -
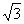 /3
/3 - sin 240° = sin (180° + 60°) = - sin 60° = -
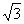 /2
/2 - cos (-240°) = cos (-270° + 30°) = - sin 30° = - 1/2
- sin 330° = sin (270° + 60°) = - cos 60° = - 1/2
- cos (-330°) = cos (-360° + 30°) = cos 30° =
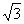 /2
/2
Задача 2. Упростить выражение 
Решение:
Упростим второй и третий члены выражения.
· 
Задача 3. Упростить выражение:
· 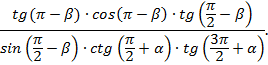
Решение:
· 1) 
· 2) 
· 3) 
· 4) 
· 5) 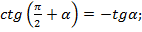
· 6) 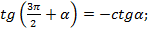
7) 
· 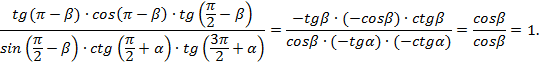
Ответ: 1.
Задача 4. Вычислить 
Решение:
· 
1. 
· 
2. 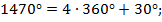
· 
3. 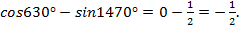
Ответ: 
Пример 1.
Вычислить  .
.
Решение:
·  .
.
Значение последнего синуса можно вычислять, а можно и не вычислять в зависимости от поставленной задачи. Очевидно, что калькулятор способен вычислить с одинаковым успехом и  , и
, и  .
.
Пример 2.
Вычислить  .
.
Решение:
· 
 .
.
В следующем примере аргумент является отвлеченным числом, которое при решении выразим через 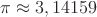 , чтобы исключить из аргумента периоды.
, чтобы исключить из аргумента периоды.
Пример 3.
Вычислить  .
.
Решение:
 .
.
Тест по теме
Тригонометрические функции
1. Найдите значение выражения: 
1)  ; 2)
; 2) 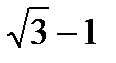 ; 3)
; 3) 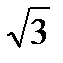 ; 4) 0.
; 4) 0.
2. Сравните с нулём выражения: sin 1200, cos 1950, ctg 3590.
Выберите правильную серию ответов:
1) + – – 2) – – + 3) + + – 4) + – +
3. Вычислите: 
1) 12; 2)  ; 3) 6; 4) 0.
; 3) 6; 4) 0.
4. Упростите выражение: 
1) – cos2a; 2) cos2a; 3) sin2a; 4) – sin2a.
5. Упростите выражение: sina * cos a * ctg a – 1
1) 0; 2) cos2a; 3) – sin2a; 4) sin2a.
6. Упростите выражение: 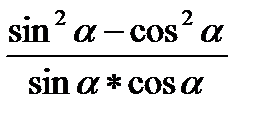
sin a – cos a; 2) –2 ctg 2a; 3) tg 2a; 4) 0,5 ctg 2a.
7. Вычислите: 2sin 150 * cos 150
1) 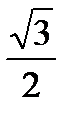 ; 2)
; 2) 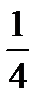 ; 3)
; 3)  ; 4)
; 4)  .
.
8. Вычислите: cos 
1)  ; 2)
; 2) 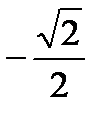 ; 3)
; 3)  ; 4) 0.
; 4) 0.
9. Представив 1050 как 600 + 450, вычислите sin 1050.
1) 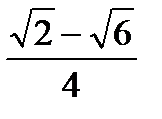 ; 2)
; 2)  ; 3)
; 3) 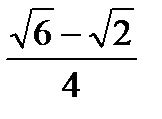 ; 4)
; 4) 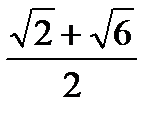 .
.
10. Дано: sin a = –  где
где  . Найдите tg 2a
. Найдите tg 2a
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
 2020-05-11
2020-05-11 472
472






