Two collinear vector may point in either same or opposite direction. But, they cannot be inclined at some angle from each other for sure. They are commonly used not only in mathematics, but in physics, engineering and technology as well.
The word collinear is formed by combining two words - co and linear. The word "co" here refers to "same" and "linear" means "in a line". It means collinear literally means something which remains in the same line.
If two vectors lie along the same line, then they are known as collinear vectors. In mathematical language, any two parallel vectors are also called collinear vectors, since they point in either exactly same or exactly opposite direction. Thus, two vectors are said to be collinear if and only if they are either along same line or are parallel to each other.
Collinear vectors either are directed in the same direction, or in the opposite direction. If the direction 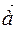 of the direction
of the direction 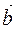 is the same, it is designated so
is the same, it is designated so 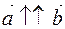 , if the direction of the direction is set in the opposite direction, then denoted
, if the direction of the direction is set in the opposite direction, then denoted 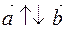 . The zero vector is oriented to any vector.
. The zero vector is oriented to any vector.
Definition. Nonzero vectors having the same directions and equal lengths are called equal vectors. All zero vectors are considered equal.
And then, if they 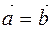 are equal, then it must be first
are equal, then it must be first 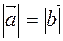 , secondly
, secondly 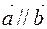 , in the third
, in the third 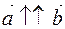 place.
place.
And vectors  and
and 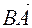 are opposite vectors. They will have the right equality for them
are opposite vectors. They will have the right equality for them 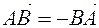 .
.
From the definition of the equality of vectors, the following conclusions are drawn:
1. You can copy vectors to any point in space. Therefore, free vectors are considered in analytic geometry;
2. Collinear vectors can be copied into one straight line;
3. Any two vectors can be copied into one plane;
4. For a vector 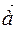 and a point 0 there is only one point M for which it is true
and a point 0 there is only one point M for which it is true 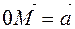 . It is said that the point M is drawn by the point vector
. It is said that the point M is drawn by the point vector 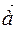 by measuring the length of the vector from the point 0.
by measuring the length of the vector from the point 0.
 If the vector
If the vector 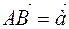 is drawn from point 0 or the vector
is drawn from point 0 or the vector 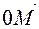 is obtained from the parallel displacement of the vector
is obtained from the parallel displacement of the vector 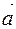 (Figure 2), then the vectors
(Figure 2), then the vectors 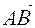 are
are 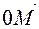 not different, they are equal and vectors that represent only one vector
not different, they are equal and vectors that represent only one vector 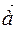 , constructed from point A and from point 0.
, constructed from point A and from point 0.
Аddition of vectors
Let any two vectors 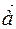 and
and 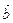 in the plane be given.
in the plane be given.
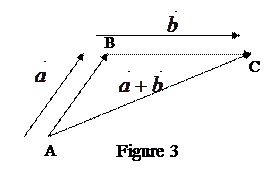 Definition. Adding the given
Definition. Adding the given 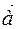 and
and 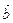 vectors gives the vector
vectors gives the vector 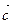 , which is obtained in this way: from any point A we postulate the vector
, which is obtained in this way: from any point A we postulate the vector 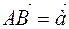 and from its and we postpone the second vector
and from its and we postpone the second vector 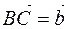 and by connecting the initial point with the final one
and by connecting the initial point with the final one 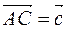 and write them as
and write them as 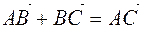 or
or 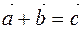 (Figure 3). Since the points are uniquely determined, the third vector, which is the sum of two vectors, is also determined by one. This method of adding vectors is a triangle method.
(Figure 3). Since the points are uniquely determined, the third vector, which is the sum of two vectors, is also determined by one. This method of adding vectors is a triangle method.
This definition is the addition of vectors, even if the points 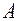 ,
, 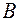 ,
, 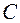 are in the plane
are in the plane
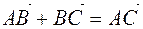 (1.1)
(1.1)
shows the correctness of the equation.
If all three points 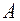 ,
,  ,
, 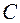 belong to one straight line, And also the case when any two of them or even three coincide (4a, b - fig.), then equality (1.1) holds.
belong to one straight line, And also the case when any two of them or even three coincide (4a, b - fig.), then equality (1.1) holds.

If you draw a triangle  from Figure 3 to a parallelogram (Figure 5), then
from Figure 3 to a parallelogram (Figure 5), then
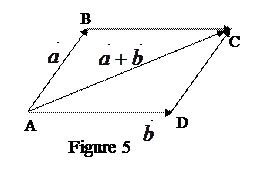
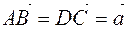 ,
, 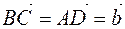 . Then it turns out
. Then it turns out 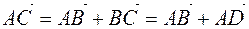 .
.
Here's a new rule for adding vectors: To add the vectors 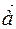 and
and 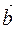 from any point, you need to measure the vectors
from any point, you need to measure the vectors 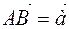 ,
, 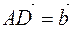 fill them to a parallelogram. The diagonal of the parallelogram from the point A is the total vector and is equal to the sum of the given vectors. This method is called the parallelogram method (parallelogram rule)
fill them to a parallelogram. The diagonal of the parallelogram from the point A is the total vector and is equal to the sum of the given vectors. This method is called the parallelogram method (parallelogram rule)
 The triangular method for vector summation can also be used for any number of two vectors. For example, for to find the sum of vectors
The triangular method for vector summation can also be used for any number of two vectors. For example, for to find the sum of vectors 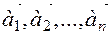 , starting with any
, starting with any 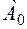 point, you need to measure the vectors
point, you need to measure the vectors 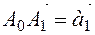 ,
, 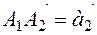 ,…,
,…, 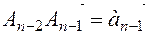 ,
, 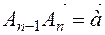 to enter (Fig. 6),...,. Then we get a vector that connects the starting point of the first vector with the final point of the last vector
to enter (Fig. 6),...,. Then we get a vector that connects the starting point of the first vector with the final point of the last vector 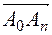 and is directed at it, the resulting vector is equal to the sum of the given
and is directed at it, the resulting vector is equal to the sum of the given 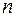 vectors
vectors
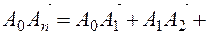
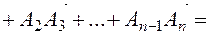
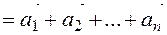 .
.
This method of summing vectors is a polygonal method.
We consider the basic properties of addition of vectors.
10 A commutative law holds for all vectors 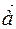 and
and 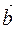 , that is
, that is 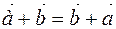 ,
,
Proof. The proof of this property follows directly from Figure 5, where the vector 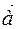 is parallelly transferred to the point
is parallelly transferred to the point 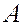 and
and 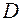 , the vector
, the vector 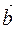 in parallel is transferred to the point A and to the point
in parallel is transferred to the point A and to the point 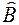 . Because of this
. Because of this 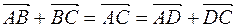 rightly, it will
rightly, it will 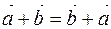 .
.
20 For any three vectors 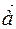 ,
, 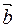 ,
, 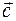 , the law (associative law) is satisfied
, the law (associative law) is satisfied
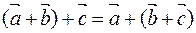 .
.
Proof. We transfer the given vectors in parallel from any point 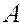 ,
, 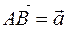 and at the end of the vector by parallel transfer
and at the end of the vector by parallel transfer 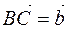 we mix the next vector, then we transfer the vector
we mix the next vector, then we transfer the vector 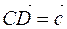 from the end of the second vector (Fig. 7). Then we obtain the following vector by the triangle method:
from the end of the second vector (Fig. 7). Then we obtain the following vector by the triangle method:
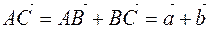 ,
,
 ,
,
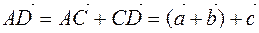
and
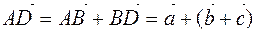 . From here
. From here 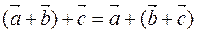 .
.
30 Equality 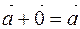 is satisfied for any vector
is satisfied for any vector 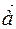 .
.
Proof. Suppose that 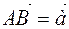 . the second connection is a zero vector, so we write it in its form
. the second connection is a zero vector, so we write it in its form 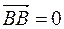 .. Then by the triangle method we have
.. Then by the triangle method we have 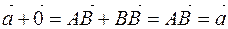 , Hence.
, Hence. 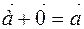
The sum of any vector and the opposite (-) vector is zero to the vector, ie E
40 The sum of any vector 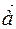 and the opposite (-
and the opposite (- 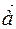 ) vector is zero vector, i.e.
) vector is zero vector, i.e. 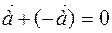
Proof: If 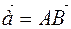 , then
, then 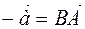 . To mean it would
. To mean it would 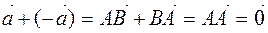 . Then,
. Then, 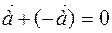 .
.
Difference of vectors
Let 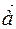 and
and 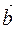 be two vectors in the plane. The difference vector or difference
be two vectors in the plane. The difference vector or difference 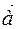 -
- 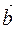 of
of 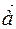 and
and 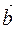 is a vector
is a vector 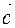 such that
such that 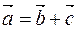 or
or 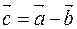 . Thus we have
. Thus we have 
In order to build difference of 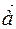 and
and 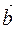 vectors (
vectors (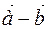 ) we transfer vectors
) we transfer vectors 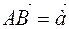 ,
, 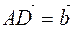 to one point
to one point  (Figure 8), moving them in parallel, we add ends. Then
(Figure 8), moving them in parallel, we add ends. Then 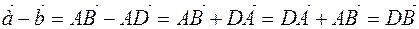 . So
. So
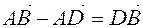 . (1.2)
. (1.2)
According to the procedure of forming the sum of vectors by setting the addends one after the other, the equation tallies with the picture below; when the minuend and the subtrahend emanate from a common initial point, their difference vector can be directed from the terminal point of the subtrahend to the terminal point of the minuend. 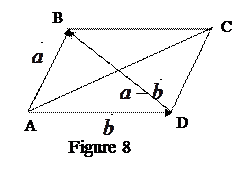 In order to build difference of
In order to build difference of 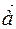 and
and 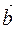 vectors (
vectors (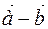 )we add
)we add 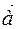 to the vector (-
to the vector (- 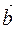 ) (Figure 8).
) (Figure 8).
Now the parallelogram rules can be generalized. If we measure vectors 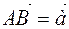 ,
, 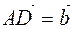 in such a way that we can deduce from one point
in such a way that we can deduce from one point 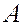 and fill it up to a parallelogram (Fig. 8), then the diagonal
and fill it up to a parallelogram (Fig. 8), then the diagonal 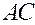 of the point
of the point 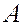 is the sum of the vectors. The vector that is equal to the second diagonal represents the difference of vectors, i.e.
is the sum of the vectors. The vector that is equal to the second diagonal represents the difference of vectors, i.e. 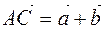 ,
, 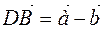 ,
, 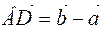 .
.
Theorem. Any two vectors have a difference and this difference is unique.
Proof: The vectors 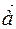 and
and 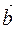 are given. We will place them in such a way as to move them parallel to themselves (Figure 8). Then
are given. We will place them in such a way as to move them parallel to themselves (Figure 8). Then 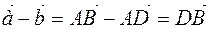 it happens. Because
it happens. Because 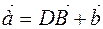 or
or 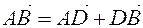 . That's why
. That's why 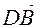 it always happens.
it always happens.
We now prove that the difference is unique. Consider the opposite. Let the difference be not unique, but two different: 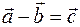 and
and 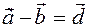 . Then by definition of the difference there must be a
. Then by definition of the difference there must be a 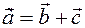 and
and 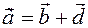 .
.
It follows from the last equality that 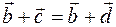 .
.
If we add the equality - 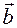 to both sides
to both sides 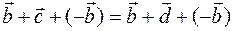 , we get
, we get 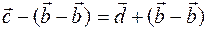 ,
, 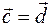 :
:
Therefore, the vectors 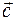 and
and 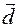 will be one vector.
will be one vector.
Multiplication of a vector by a number
Definition. The multiplication of a non-zero vector 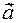 by a real number
by a real number 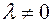 is a vector of length
is a vector of length 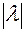
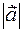 , and for
, and for 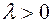 the direction of the resulting vector coincides with the direction of the given vector
the direction of the resulting vector coincides with the direction of the given vector 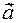 , if
, if 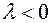 , the direction of the resulting vector is opposite to the direction of the given vector
, the direction of the resulting vector is opposite to the direction of the given vector 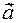 and is denoted as
and is denoted as 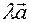 .
.
The definition implies
a) for any vector 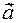 and number
and number 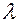 is valid:
is valid: 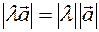
b) When the vector is multiplied by a number, we obtain a collinear vector.
From the definition of multiplication of a vector by a number, the following concepts follow:
1) the product of any vector by zero is a zero vector.
Indeed, if 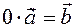 . then by definition, we get that the modulus of the vector
. then by definition, we get that the modulus of the vector 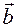 must be
must be 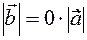 .
.
The right-hand side of the equation is zero. Hence, the vector 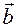 is a zero vector. To mean
is a zero vector. To mean 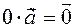 .
.
2) The product of the zero vector by any number is zero vector.
Indeed, by definition 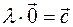 and
and 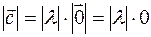 there is a modulus of the vector
there is a modulus of the vector 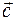 .
.
The right side is zero. Therefore, the vector 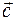 is zero. Thus we obtain:
is zero. Thus we obtain: 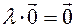 .
.
3) The ratio of any vector to its modulus is equal to the zero vector, with the direction that aligns with itself.
Indeed, let any vector 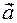 and a unit vector
and a unit vector 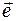 with the same direction with it be given. Then this will by definition be multiplication of the vector by a number
with the same direction with it be given. Then this will by definition be multiplication of the vector by a number 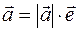 . This will be multiplied by a number
. This will be multiplied by a number 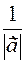 , then
, then 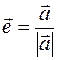 The vector is a unit vector
The vector is a unit vector 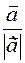 . It is called the unit vector or ortvector of vector
. It is called the unit vector or ortvector of vector 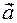 and is denoted by
and is denoted by 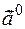 . So
. So 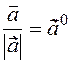 , it's possible
, it's possible 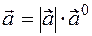 . We obtain the same
. We obtain the same 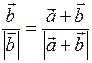 is unit vector.
is unit vector.
Multiplication of a vector by a number has the following properties:
10 For any vector 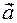 , the following will be true:
, the following will be true: 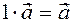 (the special role of the number 1);
(the special role of the number 1);
20 For any numbers 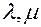 and a vector
and a vector 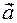 , the following is true:
, the following is true: 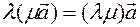 (commutative property of the numerical factor);
(commutative property of the numerical factor);
30 for any number 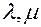 and vector
and vector 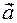 , the following is true:
, the following is true: 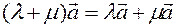 (multiplicative distribution coefficient);
(multiplicative distribution coefficient);
40 For any number 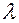 and vectors
and vectors 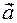 ,
, 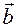 the following is true:
the following is true:  (the distribution property with respect to the sum of the vectors);
(the distribution property with respect to the sum of the vectors);
The proof of property 10 is derived directly from the definition of the product of a number and a vector.
Indeed, the vector 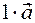 and vector
and vector 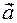 modules are equal to
modules are equal to 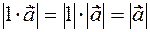 and
and 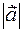 . Their directions are the same. That's it's by definition
. Their directions are the same. That's it's by definition 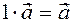 and
and 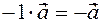 It is clear that these modules are the same
It is clear that these modules are the same 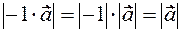 and
and 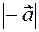 their orientation is the same. That's why
their orientation is the same. That's why 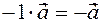 .
.
20 - proof of ownership. If 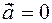 or
or 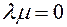 true or equal
true or equal 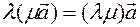 , the equality is obvious, since both sides of the equation are zero to vectors. Now let's be
, the equality is obvious, since both sides of the equation are zero to vectors. Now let's be 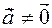 ,
, 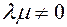 . in the near future
. in the near future 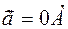 . Then the vectors
. Then the vectors 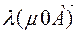 and
and 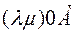 will lie along the line
will lie along the line 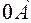 and be equal to the lengths
and be equal to the lengths 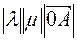 . And when it is oriented
. And when it is oriented 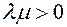 with the vector
with the vector 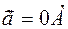 , it will be
, it will be 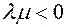 in the opposite direction
in the opposite direction 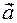 . The way it is
. The way it is 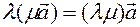 . Thus, property 20 is proved. All other properties are proved.
. Thus, property 20 is proved. All other properties are proved.
Example 1 Given a rhombus 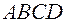 ,
, 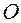 it will be the intersection of its diagonals. In this equation: а)
it will be the intersection of its diagonals. In this equation: а) 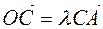 ; б)
; б) 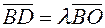 ; в)
; в) 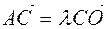 ; г)
; г) 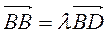 find the multiplier
find the multiplier 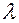 (figure 9).
(figure 9).
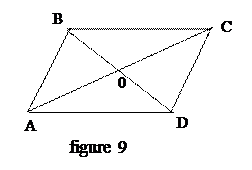 а)
а) 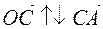 ,
, 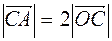 for the reason
for the reason 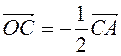 ,.
,. 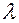 ,
, 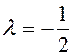
b) 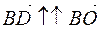 ,
, 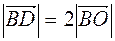 , that is
, that is 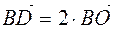 , it will
, it will 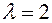 .
.
c) 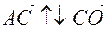 ,
, 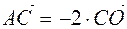 , as it happens
, as it happens 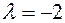 .
.
d) 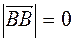 ,
, 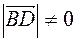 , since this happens
, since this happens 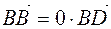 ,
, 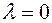 .
.
Theorem (collinear sign). In order that the vector 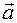 and the non-zero vector
and the non-zero vector 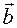 are collinear it is necessary and sufficient that there exist only one real number
are collinear it is necessary and sufficient that there exist only one real number 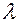 satisfying the equation
satisfying the equation
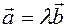 (1.3)
(1.3)
Proof:
Necessity. Let the vector 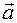 be collinear with a nonzero vector
be collinear with a nonzero vector 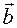 . There are three possible situations:
. There are three possible situations: 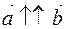 ,
,  ,
, 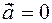 .
.
If 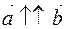 , then
, then 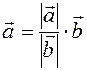 . that is, then the equation (1.3) is satisfied for
. that is, then the equation (1.3) is satisfied for 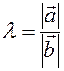 .
.
If 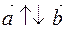 , then
, then 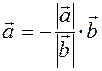 . that is, then the equation (1.3) is satisfied for
. that is, then the equation (1.3) is satisfied for 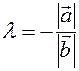 .
.
If 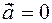 , then
, then 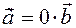 . that is, then the equation (1.3) is satisfied for
. that is, then the equation (1.3) is satisfied for 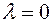 .
.
Sufficiency If equation (1.3) is satisfied for a real number 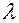 , then by definition multiplication of the vector by a number and by the definition of collinear vectors we obtain that the vector
, then by definition multiplication of the vector by a number and by the definition of collinear vectors we obtain that the vector 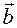 is collinear to the vector
is collinear to the vector 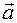 .
.
Suppose that there is one more number 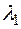 satisfying the conditions of the theorem. Then
satisfying the conditions of the theorem. Then 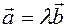 and
and 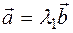 so on
so on 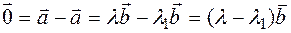 . Because
. Because 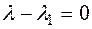 or
or 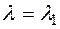 of this
of this 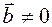 .
.
And then 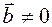 , so on
, so on 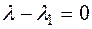 or
or 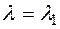 .
.
Example. prove that these vectors 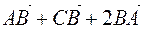 and
and 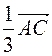 . are collinear.
. are collinear.
Decision. We use the properties of vectors and get the correctness 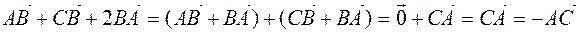 . So, the vectors
. So, the vectors 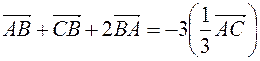 are collinear
are collinear
1.2 Linear dependence and linear independence of vectors
Let there be given a vector system 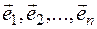 of
of 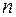 vectors. An expression of this type
vectors. An expression of this type 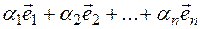 (where
(where 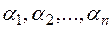 any real number) is a linear combination of the given vector system, and the numbers
any real number) is a linear combination of the given vector system, and the numbers 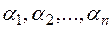 are its coefficients. For example,
are its coefficients. For example, 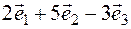 there is a linear combination of vectors
there is a linear combination of vectors 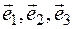 , its coefficients is
, its coefficients is  . A linear combination of a given vector system defines one specific vector that is
. A linear combination of a given vector system defines one specific vector that is 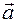 vector:
vector:
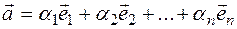 . (1.4)
. (1.4)
Thus, the vector 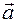 is a linear combination of the vectors
is a linear combination of the vectors 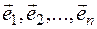 or is decomposed into vectors
or is decomposed into vectors 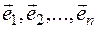 or linearly expressed in terms of the vectors
or linearly expressed in terms of the vectors 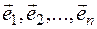 .
.
Definition. If there is at least one of them a nonzero number such 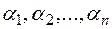 . and the equality holds
. and the equality holds
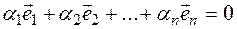 (1.5)
(1.5)
Then, the system of vectors 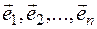 is called linear dependent
is called linear dependent
From this definition, if the given vector system is linearly dependent, then one of them will be equal to the linear combination of the others.
Indeed, if (1.5) is not equal to 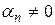 , then
, then
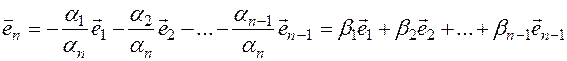
will be. On the contrary, it is true that a linear combination of a given system of vectors is a linear dependent system.
Definition. If equation (1.5) is true 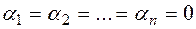 , then only in this case the system of vectors
, then only in this case the system of vectors 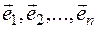 is linearly independent.
is linearly independent.
If at least one of the vectors 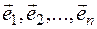 is a zero vector, then it is difficult to see that the vector system is linearly dependent. Indeed, for one, for example, if
is a zero vector, then it is difficult to see that the vector system is linearly dependent. Indeed, for one, for example, if 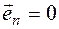 6 then (5.2) is true for case
6 then (5.2) is true for case 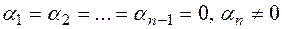 , then it is satisfied
, then it is satisfied 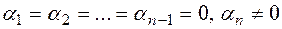 . Hence, by definition, vectors
. Hence, by definition, vectors 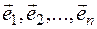 are linearly dependent. Then there is no zero vector in the system of linear independent vectors.
are linearly dependent. Then there is no zero vector in the system of linear independent vectors.
Theorem 1. In order for two vectors to be linearly dependent, their collinearity is necessary and sufficient.
Consequence. Two non-collinear vectors will be linearly non-independent.
Definition. Vectors belonging to the same plane or vectors belonging to parallel planes refer to the coplanar vectors.
Theorem 2. In order for three vectors to be linearly dependent, their coplanarity is necessary and sufficient.
Consequence. not coplanar three vectors will be linearly independent.
Theorem 3. In space, any four vectors will be linearly dependent.
Expansion of the vector into two noncollinear vectors in the plane. Basis of the plane.
Theorem. Any self-coplanar vector 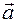 can be decomposed into vectors
can be decomposed into vectors 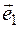 ,
, 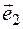 that are not mutually collinear, and this will be the only decomposition.
that are not mutually collinear, and this will be the only decomposition.
Evidence. 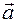 ,
,  ,
, 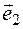 - vectors are coplanar and,
- vectors are coplanar and,  ,
, 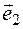 - Let not collinear vectors. Since these vectors are coplanar, they will be in the same plane if you transfer them in parallel so that their start points coincide in one point. They will lie in the same plane. Therefore, according to Theorem 2, they are linearly dependent.
- Let not collinear vectors. Since these vectors are coplanar, they will be in the same plane if you transfer them in parallel so that their start points coincide in one point. They will lie in the same plane. Therefore, according to Theorem 2, they are linearly dependent.
Consequently, 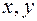 there are real numbers and the equality
there are real numbers and the equality 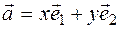 holds. Thus, the vector
holds. Thus, the vector 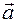 is decomposed as follows
is decomposed as follows  and
and 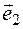 . We now prove that this decomposition is unique. Let's take the opposite, We will assume that the vector
. We now prove that this decomposition is unique. Let's take the opposite, We will assume that the vector 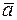 decomposes as follows
decomposes as follows 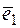 and
and 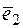 :
: 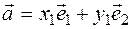 So
So 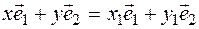 it will be
it will be 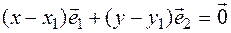 . But, according to the hypothesis of the theorem, they
. But, according to the hypothesis of the theorem, they 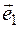 and
and 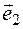 are not collinear. Therefore, they are linearly independent. Therefore, the last equation
are not collinear. Therefore, they are linearly independent. Therefore, the last equation 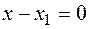 ,
, 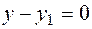 must be fulfilled only after this
must be fulfilled only after this 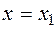 ,
, 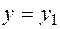 . Thus, it is not true that
. Thus, it is not true that 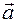 vector can be decomposed into two different types. Thus, if
vector can be decomposed into two different types. Thus, if 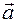 ,
, 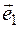 ,
, 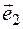 there is a complanar,
there is a complanar,  ,
, 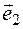 there is no coincidence, then
there is no coincidence, then 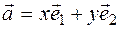 its equality is fulfilled.
its equality is fulfilled.
Definition A basis of a plane is any two vectors of this plane that can be obtained in a certain order and are not collinear to each other, a plane.
Since there are many such pairs of vectors in the plane, there are infinitely many planes in the plane. The differences between them are in the vectors that form the basis. Vectors forming a basis refer to the basis vectors. If  ,
, 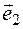 there are basis vectors, then the first basic vector is
there are basis vectors, then the first basic vector is  , the
, the 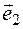 is the second base vector. Then (
is the second base vector. Then (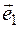 ,
, 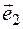 ) and (
) and (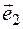 ,
, 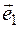 ) there are different bases. The base (
) there are different bases. The base ( ,
,  ) is given.
) is given.  and
and  this is a small rotation angle counterclockwise, to match the direction. If the directions coincide with the direction counterclockwise, then this direction is considered right, if on the contrary, ie. clockwise-left direction.
this is a small rotation angle counterclockwise, to match the direction. If the directions coincide with the direction counterclockwise, then this direction is considered right, if on the contrary, ie. clockwise-left direction.
the 10-а figure shows the right vector, the 10-б figure shows the left vector.
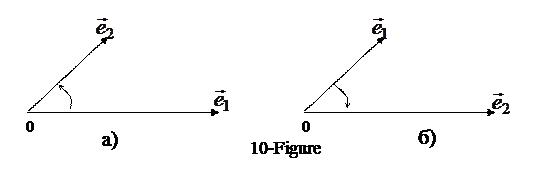
We use the right basis,
Let a basis ( ,
,  ) be given on a plane, then any vector
) be given on a plane, then any vector 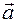 of this plane should be decomposed, according to the theorem just proved, only in a unique way onto the basis vectors:
of this plane should be decomposed, according to the theorem just proved, only in a unique way onto the basis vectors: 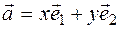 .
.
Definition. The coordinates of the vector 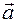 with respect to the bases (
with respect to the bases (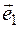 ,
, 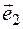 ) on the plane are the coefficients of the expansion
) on the plane are the coefficients of the expansion 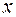 and
and 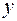 . The vector coordinates are written in parentheses. By definition
. The vector coordinates are written in parentheses. By definition 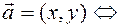
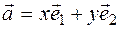 , the first coordinate of the vector
, the first coordinate of the vector 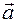 is
is 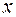 , the second coordinate of the vector -
, the second coordinate of the vector - 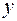 . For example: if
. For example: if 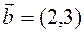 so
so 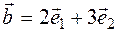 , if
, if 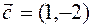 will be so
will be so 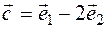 .
.
Vectors in spaces are decomposed into three vectors.
The basis in space.
Theorem. We can decompose any vector 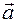 of space without coplanar vectors
of space without coplanar vectors
 ,
, 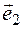 ,
, 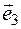 , but it can be decomposed in a single way.
, but it can be decomposed in a single way.
Evidence. Let the vectors  ,
, 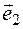 ,
, 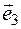 not coplanar. then they will be linearly independent. It is good that four vectors
not coplanar. then they will be linearly independent. It is good that four vectors 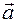 ,
,  ,
, 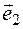 ,
, 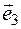 are linearly dependent by Theorem 3. Therefore, there are numbers that can not be equal to zero at the same time, and numbers
are linearly dependent by Theorem 3. Therefore, there are numbers that can not be equal to zero at the same time, and numbers 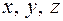 must be found, and the equation
must be found, and the equation 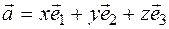 must be satisfied, i.e. Any vector
must be satisfied, i.e. Any vector  of space is not coplanar
of space is not coplanar  ,
,  ,
, 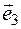 , but decomposes into vectors
, but decomposes into vectors 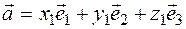 . We now prove this decomposition. For example,
. We now prove this decomposition. For example, 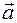 vector are classified use vectors
vector are classified use vectors  ,
, 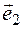 ,
, 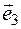 as follows
as follows 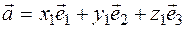 . These are two classifications of one vector
. These are two classifications of one vector
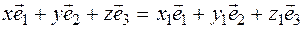
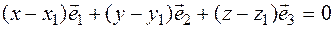
By the theorem, vectors  ,
, 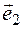 ,
, 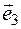 are not coplanar, therefore they are linearly independent vectors. In this regard, the last equality
are not coplanar, therefore they are linearly independent vectors. In this regard, the last equality  ,
,  and
and 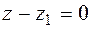 only when this is done.
only when this is done. 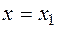 ,
, 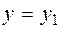 and
and 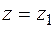 Thus,
Thus, 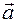 can not decompose for
can not decompose for  ,
, 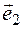 ,
, 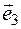 in different ways, it is wrong. In other words, the equation
in different ways, it is wrong. In other words, the equation 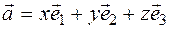 is uniquely determined.
is uniquely determined.
Definition. A spatial basis is mutually non-coplanar any three vectors.
Since there are many such pairs of vectors in the plane, there are infinitely many planes in the space. The differences between them are in the vectors that form the basis. Vectors forming a basis refer to the basis vectors. If  ,
, 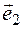 ,
, 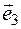 there are basis vectors, then the first basic vector is
there are basis vectors, then the first basic vector is  , the
, the 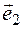 is the second base vector, then the the third basic vector is
is the second base vector, then the the third basic vector is 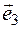 . Then (
. Then ( ,
, 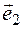 ,
, 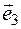 ) and (
) and (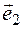 ,
,  ,
, 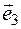 ) there are different bases. The base
) there are different bases. The base 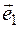 ,
, 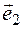 ,
, 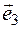 is given (11-Figure).
is given (11-Figure).  and
and 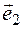 , after
, after 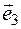 this is a small rotation angle counter clock wise, to match the direction. If the directions coincide with the direction counter clock wise, then this direction is considered right (11а-Figure), if on the contrary, i.e. clock wise-left direction(11б-Figure).
this is a small rotation angle counter clock wise, to match the direction. If the directions coincide with the direction counter clock wise, then this direction is considered right (11а-Figure), if on the contrary, i.e. clock wise-left direction(11б-Figure).
We use the right basis,
Definition. The coordinates of the vector 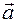 with respect to the bases (
with respect to the bases (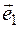 ,
, 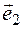 ,
, 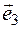 ) on the space are the coefficients of the expansion
) on the space are the coefficients of the expansion 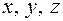 . The vector coordinates are written
. The vector coordinates are written 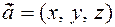 . By definition
. By definition 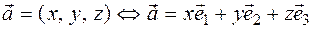 , the first coordinate of the vector
, the first coordinate of the vector 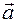 is
is 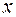 , the second coordinate of the vector -
, the second coordinate of the vector - 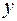 , third coordinate of the vector
, third coordinate of the vector 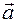 is Z
is Z
For example, ABCD parallelogram, O is the point of intersection of diagonals, 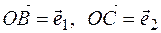 - basis vectors, find the coordinates of the sides vectors of the parallelogram and the diagonals of the parallelogram,
- basis vectors, find the coordinates of the sides vectors of the parallelogram and the diagonals of the parallelogram,

Decision. To solve the problem, we must write the sides  and
and  of the parallelogram, respectively, through the expansion of the vectors, the diagonal through the expansion of the vectors. from the triangle Δ ОВС
of the parallelogram, respectively, through the expansion of the vectors, the diagonal through the expansion of the vectors. from the triangle Δ ОВС
For example, ABCD parallelogram, O is the point of intersection of diagonals, -basis vectors, find the coordinates of the vectors of the parallelogram and the diagonals of the parallelogram,
Decision. To solve the problem, we must write the sides of the parallelogram, respectively, through the expansion of the vectors, the diagonal through the expansion of the vectors. from the triangle ABC we find:
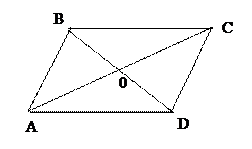
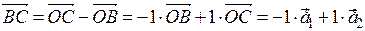 . Then
. Then 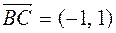 .
. 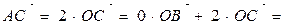
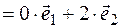 .
.
From here 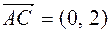 .
. 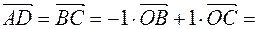
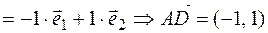
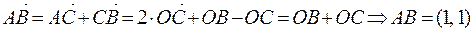 ;
; 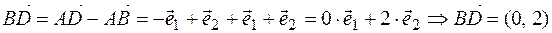 ;
; 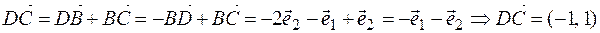 .
.
Example 2. Find the coordinates of the basis vector.
Decision. To find the coordinates  of the basis (
of the basis ( ,
, 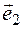 ,
, 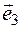 ), we must
), we must 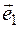 classify the base vectors. It is classified as follows
classify the base vectors. It is classified as follows 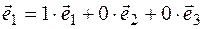 . That's why
. That's why 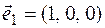 . In the same way
. In the same way 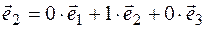 and
and 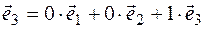 it will happen
it will happen 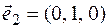 ,
, 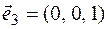 . It is clear that only one (
. It is clear that only one (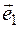 ,
, 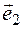 ,
,  ) base is given by coordinates,
) base is given by coordinates, 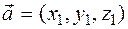 and
and 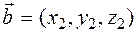 vectors are equal to their coordinates and only then are equal to each other
vectors are equal to their coordinates and only then are equal to each other
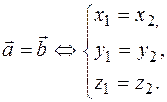
The application of arithmetic operations to vectors with coordinates,
Let the space basis ( ,
, 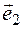 ,
, 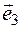 ) be given. Let
) be given. Let 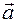 and
and 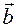 it be the coordinates of the basis
it be the coordinates of the basis 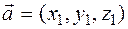 ,
, 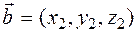 . The following assumptions about vector coordinates are true:
. The following assumptions about vector coordinates are true:
10.The sum of two or more vectors is equal to the sum of the corresponding coordinates of these vectors 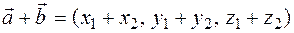 .
.
Proof. By definition, the vector coordinates will be 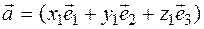 and
and 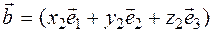 :
:
Then, depending on the properties of the addition of vectors, we have:
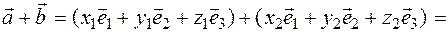
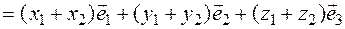
By definition:
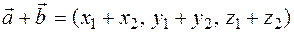
This rule is valid, if the number of vectors is greater than two
Example 1, if 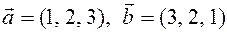 and
and 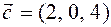 so
so 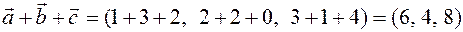 .
.
20 Differences of vectors are equal to their difference of corresponding coordinates. 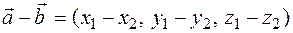
We offer independent proof to students.
30. When the vector is multiplied by a number, all its coordinates are multiplied by this number.
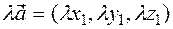
Proof. The vector 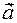 will be decomposed into basis vectors
will be decomposed into basis vectors 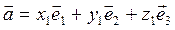 .From this we have
.From this we have
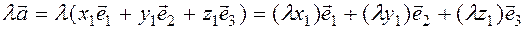
Since the coordinates of the vector
 2020-05-21
2020-05-21 285
285