Приведём другое решение

Вариант № База.

1. Найдите значение выражения

Решение.

Найдём значение выражения:

Ответ: 1.

2. Найдите значение выражения .

Решение.

Найдем значение выражения:

Ответ: 9100.

3. В школе 800 учеников, из них 30% — ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается?

Решение.

Учеников начальной школы 800 0,3 = 240, а учеников средней и старшей школы — 800 − 240 = 560. Значит, немецкий язык в школе изучают 560 0,2 = 112 учеников.

Ответ: 112.

4. Закон Гука можно записать в виде F = kx, где F — сила (в ньютонах), с которой сжимают пружину, x — абсолютное удлинение (сжатие) пружины (в метрах), а k — коэффициент упругости. Пользуясь этой формулой, найдите x (в метрах), если F = 38 Н и k = 2 Н/м.

Решение.

Выразим x и подставим значения в формулу:

Ответ: 19.

5. Найдите значение выражения: .

Решение.

Выполним преобразования:

Ответ: -3.

6. Летом килограмм клубники стоит 80 рублей. Мама купила 1 кг 200 г клубники. Сколько рублей сдачи она получит с 500 рублей?

Решение.

Найдем стоимость покупки: 1 кг 200 г клубники стоит 1,2 80 = 96 рублей. Значит, с 500 рублей мама получит сдачи 500 − 96 = 404 рубля.

Ответ: 404.

7. Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Решение.

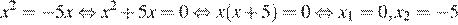
Таким образом, наименьшим корнем является:

Ответ: −5.

8. 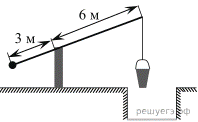На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо— 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?

Решение.

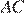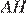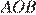Введём обозначения, приведённые на рисунке. Здесь — плечи "журавля" до опускания, — после, — высота, на которую поднялся конец короткого плеча, — высота, на которую опустился конец длинного. Рассмотрим треугольники и углы и 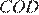равны, как вертикальные, следовательно, равны и углы при основаниях:

Следовательно, треугольники и 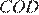подобны по двум углам, то есть

Рассмотри прямые и их пересекает секущая углы, обозначенные на рисунке 1 и 2 накрест лежащие и равны друг другу, следовательно, прямые и параллельны. Стороны углов 3 и 4 параллельны друг другу, следовательно, они равны.

Рассмотрим треугольники и они прямоугольные, имеют равные углы, следовательно, они подобны, значит:

Ответ: 3.

Примечание

Можно привести несколько иное доказательство подобия треугольников и . На приведённой ниже картинке есть два маленьких треугольника обозначенные и , они прямоугольные и одна пара углов равна друг другу как накрест лежащие при параллельных прямых, следовательно, они подобны.

Затем, можно заметить, что у треугольников и соответственные углы, не важно какие, равны друг другу, потому что их стороны параллельны, следовательно, треугольники подобны. Аналогично с треугольниками и Из трёх пар подобий этих треугольников следует, что треугольники и подобны.

9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

ВЕЛИЧИНЫ		ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) частота вращения минутной стрелки Б) частота вращения лопастей вентилятора В) частота обращения Земли вокруг своей оси Г) частота обращения Венеры вокруг Солнца		1) 1 об/день 2) 1,6 об/год 3) 24 об/день 4) 50 об/с

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

A	Б	В	Г

Решение.

Частота вращения лопастей вентилятора самая большая из предложеных велечин — 50 об/с. Частота вращения минутной стрелки — 24 об/день. Частота обращения Земли вокруг своей оси — 1 об/день. Частота обращения Венеры вокруг Солнца — 1,6 об/год.

Ответ: 3412.

10. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.

Решение.

Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (Д — Дания, Ш — Швеция, Н — Норвегия):

...Д...Ш...Н...,...Д...Н...Ш...,...Ш...Н...Д...,...Ш...Д...Н...,...Н...Д...Ш...,...Н...Ш...Д...

Дания находится после Швеции и Норвегии в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна

Ответ: 0,33.

Замечание.

Пусть требуется найти вероятность того, что датские музыканты окажутся последними среди выступающих от разных государств групп. Поставим команду Дании на последнее место и найдем количество перестановок без повторений из предыдущих групп: оно равно Общее количество перестановок из всех групп равно Поэтому искомая вероятность равна

11. На диаграмме показано распределение выплавки цинка (в тысячах тонн) в 11 странах мира за 2009 год. Среди представленных стран первое место по выплавке цинка занимало Марокко, одиннадцатое место — Болгария. Какое место занимала Греция?

Решение.

Расположим страны в порядке убывания количества выплавки цинка в год:

1) Марокко

2) Турция

3) Монголия

4) КНДР

5) Вьетнам

6) Намибия

7) Гондурас

8) Таиланд

9) Чили

10) Греция

11) Болгария

Греция находится на десятом месте

Ответ: 10.

12. На игре КВН судьи поставили следующие оценки командам за конкурсы:

Команда	Баллы за конкурс «Приветствие»	Баллы за конкурс «СТЭМ»	Баллы за музыкальный конкурс
«АТОМ»	30	21	26
«Шумы»	27	24	24
«Топчан»	28	23	25
«Лёлек и Болек»	30	22	27

Для каждой команды баллы по всем конкурсам суммируются, победителем считается команда, набравшая в сумме наибольшее количество баллов. Сколько в сумме баллов у команды-победителя?

Решение.

Посчитаем, сколько в сумме баллов у каждой команды.

«АТОМ»: 30 + 21 + 26 = 77

«Шумы»: 27 + 24 + 24 = 75

«Топчан»: 28 + 23 + 25 = 76

«Лёлек и Болек»: 30 + 22 + 27 = 79

Таким образом, командой-победителем является команда "Лёлек и Болек" с суммой 79 баллов.

Ответ: 79.

13. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Решение.

объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Ответ: 8.

14. На рисунке точками показаны объёмы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали — количество проданных обогревателей. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.

ПЕРИОДЫ ВРЕМЕНИ		ХАРАКТЕРИСТИКИ
А) зима Б) весна В) лето Г) осень		1) Ежемесячный объём продаж был меньше 40 штук в течение всего периода. 2) Ежемесячный объём продаж достиг максимума. 3) Ежемесячный объём продаж падал в течение всего периода. 4) Ежемесячный объём продаж рос в течение всего периода.

В таблице под каждой буквой укажите соответствующий номер.

А	Б	В	Г

Решение.

А) зима: из графика видно, что ежемесячный объём продаж достиг максимума (150 шт) - вариант 2

Б) весна: из графика видно, что ежемесячный объём падал в течение всего периода - вариант 3

В) лето: из графика видно, что ежемесячный объём продаж был меньше 40 штук в течение всего периода - вариант 1

Г) осень: из графика видно, что ежемесячный объём продаж рос в течение всего периода - вариант 4

Ответ: 2314

15. Основания трапеции равны 8 и 16, боковая сторона, равная 6, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Решение.

Угол в 150° образует боковая сторона и меньшее основание, тогда с большим основанием эта сторона образует угол 30°. Проведем высоту трапеции и рассмотрим прямоугольный треугольник. Из определения синуса острого угла прямоугольного треугольника получаем:

По формуле площади трапеции находим

Ответ: 36.

16. Объём конуса равен 32. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.

Решение.

Отношение объемов конусов равно кубу их коэффициента подобия k. Так как высоты конусов относятся как 1:2, то k одной второй, а значит объем отсекаемого конуса будет равен 32:2³=4.

Ответ: 4.

17. На прямой отмечены точки A, B, C и D.

Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.

ТОЧКИ		ЧИСЛА
А) A Б) B В) C Г) D		1) 2) 3) 4)

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А	Б	В	Г

Решение.

Ясно, что Заметим, что

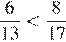, так как

Таким образом,

Ответ: 3412.

18. Какие из приведённых ниже утверждений равносильны утверждению «Если Вы ― слон, значит, Вы ничего не забываете»?

(1) Если Вы ничего не забываете, значит, Вы ― слон.

(2) Если Вы ― не слон, значит, Вы все забываете.

(3) Если Вы ― не слон, значит, Вы что-то забываете.

(4) Если Вы что-то забываете, значит, Вы ― не слон.

В ответе укажите номера выбранных Вами утверждений без пробелов, запятых и других дополнительных символов.

Решение.

1) Слоны ничего не забывают. Все остальные могут как забывать, так и не забывать.

2) То же самое, что и в первом пункте.

3) Не только слоны могут ничего не забывать.

4) Слоны ничего не забывают, поэтому это верно.

Ответ: 4.

19. Найдите трёхзначное натуральное число, большее 400, которое при делении на 6 и на 5 даёт равные ненулевые остатки и первая слева цифра которого является средним арифметическим двух других цифр. В ответе укажите какое-нибудь одно такое число.

Решение.

Число имеет одинаковые остатки при делении на 5 и на 6, следовательно, число имеет тот же остаток при делении на 30, причём этот остаток не равен нулю и меньше пяти. Таким образом, искомое число может иметь вид: .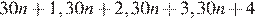

При . Ни одно из чисел не больше 400

При : 421, 422, 423, 424. Первая слева цифра не является средним арифметическим двух других цифр

При : 451, 452, 453, 454. Число 453 удовлетворяет всем условиям задачи.

Также подходят числа 573 и 693.

Ответ: 453,573, 693.

20. Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 2 раза больше наименьшего. Сколько значений может принимать величина среднего угла?

Решение.

Пусть — величина наименьшего угла, 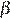— величина среднего угла, тогда — величина наибольшего угла. Полный угол равен 360°, следовательно, откуда 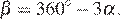Средний угол должен быть больше меньшего угла и меньше большего, то есть:

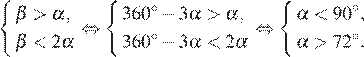
Угол 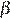— принимает только значения, измеряемые целым числом градусов, поэтому угол 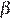может принимать 90 − 72 − 1 = 17 значений.

Ответ: 17.

Примечание.

Вычитанием единицы в последнем действии учитывается, что значения 72° и 90° не входят в число значений подсчитываемых углов.

Вариант № Профиль.

1. В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?

Решение.

В октябре виноград подорожал на 60 · 0,25 = 15 рублей и стал стоить 60 + 15 = 75 рублей. В ноябре виноград подорожал на 75 · 0,2 = 15 рублей. Значит, после подорожания в ноябре 1 кг винограда стоил 75 + 15 = 90 рублей.

Ответ: 90.

2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 27 апреля. Ответ дайте в градусах Цельсия.

Решение.

Из графика видно, что наименьшая температура воздуха 27 апреля составляла −7 °C (см. рисунок).

Ответ: −7.

3. На клетчатой бумаге с размером клетки 1 см 1 см изображён угол. Найдите его градусную величину.

Решение.

Изображённый на рисунке угол равен сумме прямого угла и угла 45°, поэтому он равен 135°.

Ответ: 135.

4. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Решение.

Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна

Ответ: 0,02.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Решение.

Область определения уравнения задается соотношением 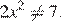На области определения имеем:

Оба найденных решения удовлетворяют условию 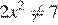, меньший из них равен −0,5.

Ответ: −0,5.

6. 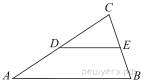Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.

Решение.

Средняя линия отсекает от треугольника подобный ему с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда

Ответ: 1.

7. На рисунке изображён график функции — производной функции f (x) определённой на интервале (1; 10). Найдите точку минимума функции f (x).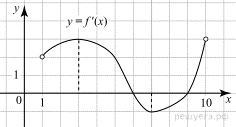

Решение.

Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. На интервале (1; 10) функция имеет одну точку минимума x = 9.

Ответ: 9.

8. Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

Решение.

Поскольку высота куба равна высоте призмы, их объемы пропорциональны площадям их оснований. Площадь основания построенной призмы в 8 раз меньше площади основания исходной, поэтому искомый объем призмы равен 12: 8 = 1,5.

Ответ: 1,5.

9. Найдите значение выражения

Решение.

Выполним преобразования:

Ответ: 1.

10. Мотоциклист, движущийся по городу со скоростью км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением км/ч Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.

Решение.

Мотоциклист будет находиться в зоне функционирования сотовой связи, если км. Задача сводится к нахождению наибольшего решения неравенства км при заданных значениях параметров и :

Учитывая то, что время — неотрицательная величина, получаем ч, то есть мин.

Ответ: 30.

11. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?

Решение.

Наименьшее общее кратное чисел 9, 14 и 18 равно 126. За 126 минут первый и второй, второй и третий, первый и третий насосы (каждый учтен дважды) заполнят 14 + 9 + 7 = 30 бассейнов. Следовательно, работая одновременно, первый, второй и третий насосы заполняют 15 бассейнов за 126 минут, а значит, 1 бассейн за 8,4 минуты.

Ответ: 8,4.

Приведём другое решение.

За одну минуту первый и второй насосы заполнят 1/9 бассейна, второй и третий — 1/14 бассейна, а первый и третий — 1/18 бассейна. Работая вместе, за одну минуту два первых, два вторых и два третьих насоса заполнят

бассейна.

Тем самым, они могли бы заполнить бассейн за 21/5 минуты или за 4,2 минуты. Поскольку каждый из насосов был учтен два раза, в реальности первый, второй и третий насосы, работая вместе, могут заполнить бассейн за 8,4 минуты.

12. Найдите точку минимума функции , принадлежащую промежутку

Решение.

Найдем производную заданной функции:

Найдем нули производной:

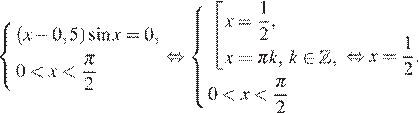
Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума

Ответ: 0,5.

13. а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

Решение.

а) Заметим, что Преобразуем уравнение:

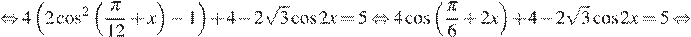
б) С помощью числовой окружности (см. рис.) отберём корни, принадлежащие отрезку Получим числа

Ответ: а) 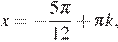где б)

14. Все рёбра правильной треугольной призмы ABCA ₁ B ₁ C ₁ имеют длину 6. Точки M и N — середины рёбер AA ₁ и A ₁ C ₁ соответственно.

а) Докажите, что прямые BM и MN перпендикулярны.

б) Найдите угол между плоскостями BMN и ABB ₁.

Решение.

а) Пусть точка H — середина AC.

Тогда

Вместе с тем,

а тогда по теореме, обратной теореме Пифагора, треугольник BMN является прямоугольным с прямым углом M.

б) Проведём перпендикуляр NP к прямой A ₁ B ₁, кроме нее NP ⊥ A ₁ A. Следовательно, NP ⊥ ABB ₁. Поэтому MP — проекция MN на плоскость ABB ₁.

Прямая BM перпендикулярна MN, тогда по теореме о трёх перпендикулярах BM ⊥ MP. Следовательно, угол NMP — линейный угол искомого угла.

Длина NP равна половине высоты треугольника A ₁ B ₁ C ₁, то есть

Поэтому

Следовательно,

Ответ: б)

15. Решите неравенство:

Решение.

Перенесём все члены в левую часть и умножим на 4:

Заметим, что поэтому Получаем: Решение неравенства: или

Ответ:

16. На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.

а) Докажите, что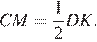

б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ ACB = 30°.

Решение.

а) Достроим треугольник ABC до параллелограмма ALBC, тогда M − точка пересечения его диагоналей.

. AL = BC = KC. AC = CD.

Тогда треугольники LAC и KCD равны по двум сторонам и углу между ними. Откуда LC = KD, а , что и требовалось доказать.

б) Пусть O₁ — центр квадрата CKFB. Тогда MO₁ — средняя линия треугольника AKB. Найдем теперь AK по теореме косинусов из треугольника ACK.

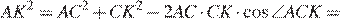
откуда

Очевидно, расстояние до другого центра сведется к нахождению DB, которое будет таким же.

Ответ:19.

17. В банк был положен вклад под 10% годовых. Через год, после начисления процентов, вкладчик снял со счета 2000 рублей, а еще через год снова внес 2000 рублей. Вследствие этих действий через три года со времени открытия вклада вкладчик получил сумму меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы он получил?

Решение.

Пусть вкладчик в банк первоначально положил х рублей. Тогда за 3 года хранения этих денег вклад вырос бы до рублей.

За первый год хранения вклада он вырос до 1,1 x рублей. Когда через год вкладчик снял 2000 рублей, на счете осталось рублей. В конце второго года хранения вклада на эту сумму были начислены проценты, вклад стал 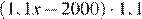рублей. Когда вкладчик снова внес 2000 рублей, сумма вклада стала равна

рублей.

К концу третьего года хранения вклада сумма увеличилась до

рублей.

Эту сумму снял вкладчик в итоге вместо первоначально запланированной 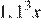рублей.

Найдем искомую разность.

рублей.

Ответ: на 220 рублей.

Примечание.

Решение можно несколько упростить, заметив, что запланированный и фактический проценты за первый год не отличаются. Пусть к началу второго года после начисления процентов на счете было х руб. Тогда запланированный процент равен 1,1² х руб., а фактический процент равен руб. Искомая разность равна 220 руб.

18. Найдите все значения а, при каждом из которых система уравнений

имеет ровно четыре различных решения.

Решение.

Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.

Рассмотрим три случая.

1) Если то получаем уравнение

Полученное уравнение задаёт параболу

2) Если то координаты любой точки прямой удовлетворяют уравнению

3) Если 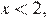то получаем уравнение

Полученное уравнение задаёт параболу

Таким образом, в первом случае мы получаем дугу 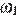параболы c концом в точке во втором — прямую l, задаваемую уравнением х = 2, в третьем — дугу параболы с концом в точке А (см. рисунок).

Рассмотрим второе уравнение системы. При каждом значении а оно задаёт прямую m, параллельную прямой или совпадающую с ней. Прямая m проходит через точку А при a = −2.

Касательная к параболе имеет с ней единственную общую точку. Запишем уравнения и как квадратные относительно x и найдем, при каких значениях параметра их дискриминанты обращаются в нуль. Тем самым, при и прямые m касаются дуг и соответственно.

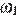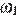Таким образом, прямая m пересекает прямую l при любом значении а, имеет одну общую точку с дугой при и имеет две общие точки с дугой при 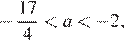имеет одну общую точку с дугой при и имеет две общие точки с дугой при

Число решений исходной системы равно числу точек пересечения прямой l и дуг 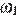и с прямой m. Таким образом, исходная система имеет ровно четыре решения при

Ответ:

19. На доске написаны числа 1, 2, 3,..., 30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек чисел, стёртых на предыдущих ходах.

а) Приведите пример последовательных 5 ходов.

б) Можно ли сделать 10 ходов?

в) Какое наибольшее число ходов можно сделать?

Решение.

а) 1-й ход (13, 14, 7), сумма 34.

2-й ход (12, 15, 6), сумма 33.

3-й ход (11, 16, 5), сумма 32.

4-й ход (10, 17, 4), сумма 31.

5-й ход (9, 18, 3), сумма 30.

б) Допустим, удалось сделать 10 ходов. Максимальные суммы, которые могли получится,

При этом были использованы все числа на доске, но сумма всех чисел с доски

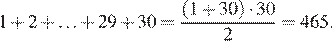
Суммы не равны, значит, 10 ходов сделать не удастся.

в) Добавим к пяти ходам пункта а) 6-й (8, 19, 2) сумма 29. Значит, 6 ходов сделать можно. Покажем, что 7 ходов сделать нельзя. Предположим, что мы сделали 7 ходов, использовав 21 число, причем получили максимальные возможные суммы 34, 33,..., 28. Таким образом, минимальная возможная сумма оставшихся 9 чисел должна быть