2020-05-21
443РАСЧЕТНО – ГРАФИЧЕСКАЯ РАБОТА
Определение законов распределения и числовых характеристик случайной величины на основе опытных данных
Выполнил:
Вариант №
Самара – 2020
Определение законов распределения и числовых характеристик случайной величины на основе опытных данных
В протокол внесено 
измерений случайной величины Х.
1. По выборке построить статистический ряд и гистограмму.
2. Вычислить числовые характеристики статистического ряда 
.
3. Выровнять статистическое распределение с помощью теоретического (нормального) закона.
Построить график теоретической (нормальной) кривой распределения 
в одной системе координат с гистограммой.
4. С помощью критерия согласия 
проверить согласованность статистического и выбранного теоретического (нормального) распределения.
Все вычисления вести с точностью до 0,0001.
- Генеральная совокупность и выборка, статистический ряд и гистограмма
Генеральной совокупностью называется совокупность всех подлежащих изучению объектов или возможных результатов всех наблюдений, производимых в одинаковых условиях над одним объектом.
Выборочной совокупностью или выборкой называется совокупность объектов или результатов наблюдений над объектом, отобранных случайным образом из генеральной совокупности.
Объемом выборки называется число объектов или наблюдений в выборке.
Конкретные значения выборки называются наблюдаемыми значениями случайной величины 
. Наблюдаемые значения заносятся в протокол, который является первичной формой записи полученного материала (Таблица 1). Для получения достоверных, надежных выводов выборка должна быть достаточно представительной по объему. В данной работе 
.
Таблица 1
| 4,18 | 4,98 | 4,59 | 3,20 | 3,67 | 3,44 | 2,90 | 4,38 | 6,08 | 3,95 |
| 5,31 | 2,97 | 6,05 | 2,53 | 2,47 | 5,70 | 2,84 | 6,32 | 1,53 | 3,46 |
| 3,97 | 1,35 | 5,08 | 3,16 | 3,36 | 4,69 | 2,36 | 0,91 | 2,05 | 3,01 |
| 4,62 | 0,87 | 2,99 | 4,45 | 4,71 | 4,36 | 3,29 | 5,98 | 0,96 | 4,01 |
| 3,63 | 4,91 | 6,21 | 4,08 | 6,44 | 4,21 | 3,23 | 4,65 | 4,03 | 4,07 |
| 5,43 | 4,16 | 1,73 | 3,72 | 3,48 | 1,87 | 2,69 | 3,89 | 3,61 | 1,75 |
| 3,40 | 5,49 | 5,12 | 1,91 | 3,70 | 4,08 | 3,95 | 3,41 | 4,57 | 4,85 |
| 3,52 | 6,10 | 1,83 | 2,72 | 5,57 | 2,27 | 4,77 | 4,78 | 5,87 | 5,60 |
| 0,80 | 5,96 | 2,54 | 1,16 | 4,05 | 4,49 | 3,25 | 2,09 | 5,56 | 4,06 |
| 5,89 | 2,89 | 2,24 | 2,29 | 1,96 | 5,04 | 1,98 | 2,89 | 1,82 | 6,95 |
Большая выборка представляет собой неупорядоченное множество чисел. Выборку приводят к наглядному упорядоченному виду. Для этого в протоколе находят наибольшее и наименьшее значения случайной величины 
: 
и 
.
Размахом выборки называется разность между наибольшим и наименьшим значениями случайной величины :
.
Размах выборки разбивают на 
интервалов (разрядов). Число разрядов устанавливают в зависимости от величины размаха выборки от 8 до 25. В этой работе примем k = 10.
Тогда длина интервала равна:
.
В протоколе подсчитаем число наблюдаемых значений случайной величины , попавших в каждый интервал. Обозначим их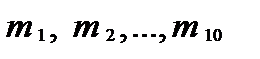 
, где 
.
Назовем 
частотой попадания случайной величины в 
-ый интервал. Если какое-либо наблюдаемое значение случайной величины совпадает с концом интервала, то это значение случайной величины по договоренности относят в один из интервалов – левый или правый.
После того как найдены частоты попадания случайной величины в -ый интервал, определяют частости случайной величины :
.
Заметим, что 
- условие полноты.
Найдем середину каждого интервала: 
.
Таблица значений границ интервалов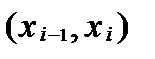 
и соответствующих частостей 
, 
попадания случайной величины в -ый интервал называется статистическим рядом (Таблица 2).
Графическое изображение статистического ряда называется гистограммой (Рисунок 1).
Она строится следующим образом: в прямоугольной системе координат по оси абсцисс откладываются значения границ интервалов и на каждом интервале как на основании строится прямоугольник высоты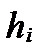 
, площадь которого равна соответствующей частости .
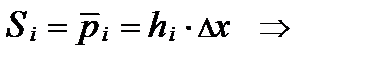
- высота -го прямоугольника, .
Таблица 2
| Номер интервала | Границы
интервала
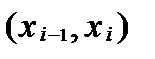
| Середина
интервала
| Частота
интервала
| Частость
интервала
| Высота
прямоугольника
|
| 1 | (0,8; 1,415) | 1,1075 | 6 | 0,06 | 0,0976 |
| 2 | (1,415; 2,03) | 1,7225 | 9 | 0,09 | 0,1463 |
| 3 | (2,03; 2,645) | 2,3375 | 9 | 0,09 | 0,1463 |
| 4 | (2,645; 3,26) | 2,9525 | 13 | 0,13 | 0,2114 |
| 5 | (3,26; 3,875) | 3,5675 | 13 | 0,13 | 0,2114 |
| 6 | (3,875; 4,49) | 4,1825 | 17 | 0,17 | 0,2764 |
| 7 | (4,49; 5,105) | 4,7975 | 14 | 0,14 | 0,2276 |
| 8 | (5,105; 5,72) | 5,4125 | 8 | 0,08 | 0,1301 |
| 9 | (5,72; 6,335) | 6,0275 | 9 | 0,09 | 0,1463 |
| 10 | (6,335; 6,95) | 6,6425 | 2 | 0,02 | 0,0325 |
|
| 
| 
| |||
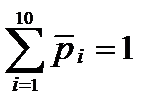
Рисунок 1
- Числовые характеристики статистического ряда
Рассмотрим следующие числовые характеристики статистического ряда:
- статистическое математическое ожидание,
- статистическая дисперсия,
-статистическое среднее квадратическое отклонение.
Статистическим математическим ожиданием или статистическим средним называется среднее арифметическое наблюдаемых значений случайной величины Х:
(1)
Статистической дисперсией называется среднее арифметическое значение величины 
:
(2)
При большом объеме выборки вычисления по формулам (1) и (2) приводят к громоздким выкладкам. Для упрощения расчетов используют статистический ряд с границами 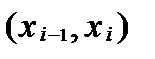и частостями , . Находят середины интервалов .
Затем все элементы выборки, которые попали в интервал 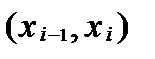, заменяют единственным значением 
. Тогда в формулах (1) и (2) вместо различных значений будет одинаковых значений.
,
,
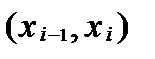где - середина интервала , - частость интервала , .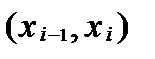
Итак, числовые характеристики статистического ряда будем находить по следующим формулам:
,
,
.
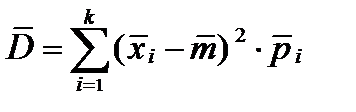Вычисление числовых характеристик статистического ряда оформим в виде таблицы 3.
Таблица 3
| Номер интервала | Середина
интервала
| Частость
| 
| 
| 
|
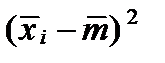
| 1 | 1,1075 | 0,06 | 0,0665 | 7,0913 | 0,4255 |
| 2 | 1,7225 | 0,09 | 0,1550 | 4,1941 | 0,3775 |
| 3 | 2,3375 | 0,09 | 0,2104 | 2,0533 | 0,1848 |
| 4 | 2,9525 | 0,13 | 0,3838 | 0,6690 | 0,0870 |
| 5 | 3,5675 | 0,13 | 0,4638 | 0,0412 | 0,0054 |
| 6 | 4,1825 | 0,17 | 0,7110 | 0,1698 | 0,0289 |
| 7 | 4,7975 | 0,14 | 0,6717 | 1,0548 | 0,1477 |
| 8 | 5,4125 | 0,08 | 0,4330 | 2,6963 | 0,2157 |
| 9 | 6,0275 | 0,09 | 0,5425 | 5,0943 | 0,4585 |
| 10 | 6.6425 | 0,02 | 0,1329 | 8,2487 | 0,1650 |
| Статистическое математическое ожидание | 3,7705 | ||||
| Статистическая дисперсия | 2,0958 | ||||
| Статистическое среднее квадратическое отклонение | 1,4477 | ||||
определяет положение центра группировки наблюдаемых значений случайной величины.
, характеризуют рассеяние наблюдаемых значений случайной величины вокруг .
- Выравнивание (сглаживание) статистического ряда с помощью нормального закона
При обработке статистического материала приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую только существенные черты статистического материала, а не случайности, связанные с недостаточным объемом экспериментальных данных. Эта задача называется задачей сглаживания или выравнивания статистического ряда. Задача выравнивания состоит в том, чтобы подобрать теоретическую кривую распределения, наилучшим образом описывающую данное статистическое распределение.
Случайная величина - есть результат измерения некоторой физической величины прибором, и представляет собой сумму точного значения физической величины и случайной ошибки измерительного прибора. Случайные ошибки прибора имеют суммарную природу и поэтому распределены по нормальному закону. Следовательно, можно предположить, что случайная величина также имеет нормальное распределение с плотностью вероятности
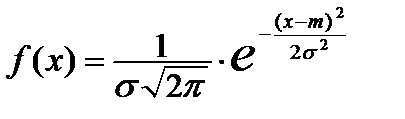, где 
.
Параметры 
и 
определяют так, чтобы числовые характеристики теоретического распределения были равны соответствующим числовым характеристикам статистического распределения, то есть 
. Тогда плотность вероятности нормального закона примет вид:
.
Нормальная (выравнивающая) кривая строится по точкам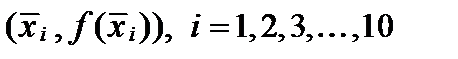 
(Рисунок 1).
Вычисления сведем в таблицу 4.
Таблица 4
| Номер интервала | Середина
интервала
| 
| 
(Приложение 1)
| 
|
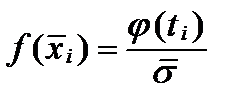
| 1 | 1,1075 | -1,8395 | 0,0735 | 0,0508 |
| 2 | 1,7225 | -1,4146 | 0,1467 | 0,1013 |
| 3 | 2,3375 | -0,9898 | 0,2444 | 0,1688 |
| 4 | 2,9525 | -0,5650 | 0,3401 | 0,2349 |
| 5 | 3,5675 | -0,1402 | 0,3950 | 0,2729 |
| 0 | 0,3989 | 0,2756 | |
| 6 | 4,1825 | 0,2846 | 0,3831 | 0,2646 |
| 7 | 4,7975 | 0,7094 | 0,3102 | 0,2143 |
| 8 | 5,4125 | 1,1343 | 0,2097 | 0,1448 |
| 9 | 6,0275 | 1,5591 | 0,1183 | 0,0817 |
| 10 | 6,6425 | 1,9839 | 0,0558 | 0,0385 |
4. Статистическая проверка гипотез. Критерий согласия
Во многих случаях закон распределения случайной величины неизвестен, но на основании опытных данных делается предположение о виде закона распределения случайной величины . Однако для окончательного решения вопроса о виде распределения следует проверить, согласуются ли результаты наблюдений с высказанным предположением. При этом если даже предположение о виде распределения сделано правильно, закон распределения наблюдаемой случайной величины будет отличаться от теоретического закона. Поэтому следует выяснить, является ли расхождение между статистическим и теоретическим законами распределения следствием ограниченного числа наблюдений или оно является чем-то более существенным, то есть на самом деле случайная величина подчинена другому закону распределения. Для решения этой задачи служит критерий согласия.
Идея применения критерия согласия состоит в том, что на основании статистического материала проводится проверка гипотезы о том, что исследуемая случайная величина подчинена некоторому определенному закону распределения, например, нормальному, показательному и т.д.
Наиболее часто для проверки гипотезы о законе распределения случайной величины применяется критерий согласия Пирсона или критерий 
.
Для проверки того, что статистическое распределение случайной величины согласуется с теоретическим (нормальным) распределением, вычисляют величину:
,
где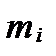 
- частота - го интервала (из Таблицы 1),
- объем выборки ( =100),
- теоретическая вероятность попадания случайной величины в интервал :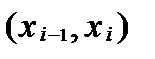
,
где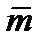 
- статистическое математическое ожидание,
- статистическое среднее квадратическое отклонение,
- границы интервалов, ,
- функция Лапласа, значения которой находят из таблицы (Приложение 2).
Значение зависит от числа степеней свободы 
,
где 
- число интервалов,
3 – число связей, наложенных при выборе теоретического (нормального) закона распределения
, 
, 
.
Замечание: Частота mi каждого интервала 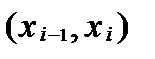должна быть не менее 5 – 8. Если это условие не выполняется, то малочисленные интервалы следует объединить в один интервал или присоединить к соседнему интервалу, суммируя частоты.
Определим число степеней свободы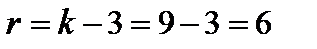 
.
Число интервалов 
, т.к. два последних интервала были объединены в один в силу их малочисленности.
Вычисления сведем в Таблицу 5.
Таблица 5
Границы
интервалов
| 
| 
(Приложение2)
| 
| 
| 
| 
|
| 0,8 | -2,0519 | -0,4799 | 0,0318 0,0628 0,1038 0,1437 0,1666 0,1616 0,1313 0,0893 0,0750 | 6 9 9 13 13 17 14 8 11 | 3,1800 6,2800 10,3800 14,3700 16,6600 16,1600 13,1300 8,9300 7,5000 | 2,5008 1,1781 0,1835 0,1306 0,8041 0,0437 0,0576 0,0969 0,8333 |
| 1,415 | -1,6270 | -0,4481 | ||||
| 2,03 | -1,2022 | -0,3854 | ||||
| 2,645 | -0,7774 | -0,2815 | ||||
| 3,26 | -0,3526 | -0,1378 | ||||
| 3,875 | 0,0722 | 0.0288 | ||||
| 4,49 | 0,4970 | 0,1904 | ||||
| 5,105 | 0,9219 | 0,3217 | ||||
| 5,72 | 1,3467 | 0,4110 | ||||
| 6,95 | 2.1963 | 0,4860 | ||||
| | 5,8286 | |||||
Для составлены таблицы (Приложение 3), из которых по найденному значению и числу степеней свободы 
находят вероятность 
. Если 
, то гипотезу о выборе теоретического закона распределения следует пересмотреть. Если 
, то статистический и теоретический законы распределения наблюдаемой случайной величины согласованы.
Замечание: Вывод о правдоподобности выдвинутой гипотезы ни в коем случае не следует понимать как достоверное свидетельство того, что гипотеза верна. Этот вывод означает только то, что гипотеза не противоречит опытным данным (не более того).
По найденному значению 
и числу степеней свободы 
по таблице вероятностей (Приложение 3) получим искомое значение вероятности 
.
Вывод: статистический и теоретический законы распределения случайной величины согласуются, следовательно, нормальное распределение может быть принято в качестве аппроксимирующего закона.
Приложение 1
Таблица значений функции 
|
| Сотые доли | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0 | 0,3989 3970 3910 3814 3683 3521 3332 3123 2897 2661 2420 2179 1942 1714 1497 1295 1109 0940 0790 0656 0540 0440 0355 0283 0224 0175 0136 0104 0079 0060 0044 0033 0024 0017 0012 0009 0006 0004 0003 0002 0001 | 0,3989 3965 3902 3802 3668 3503 3312 3101 2874 2637 2396 2155 1919 1691 1476 1276 1092 0925 0775 0644 0529 0431 0347 0277 0219 0171 0132 0101 0077 0058 0043 0032 0023 0017 0012 0008 0006 0004 0003 0002 0001 | 0,3989 3961 3894 3790 3653 3485 3292 3079 2850 2613 2373 2131 1895 1669 1456 1257 1074 0909 0761 0632 0519 0422 0339 0270 0213 0167 0129 0099 0075 0056 0042 0031 0022 0016 0012 0008 0006 0004 0003 0002 0001 | 0,3988 3956 3885 3778 3637 3467 3271 3056 2827 2589 2347 2107 1872 1647 1435 1238 1057 0893 0748 0620 0508 0413 0332 0264 0208 0163 0126 0096 0073 0055 0040 0030 0022 0016 0011 0008 0005 0004 0003 0002 0001 | 0,3986 3951 3876 3765 3621 3448 3251 3034 2803 2565 2323 2083 1849 1626 1415 1219 1040 0878 0734 0608 0498 0404 0325 0258 0203 0158 0122 0093 0071 0053 0039 0029 0021 0015 0011 0008 0005 0004 0003 0002 0001 | 0,3984 3945 3867 3752 3605 3429 3230 3011 2780 2541 2299 2059 1826 1604 1394 1200 1023 0863 0721 0596 0488 0396 0317 0252 0198 0154 0119 0091 0069 0051 0038 0028 0020 0015 0010 0007 0005 0004 0002 0002 0001 | 0,3982 3939 3857 3739 3589 3410 3209 2989 2756 2516 2275 2036 1804 1582 1374 1182 1006 0848 0707 0584 0478 0387 0310 0246 0194 0151 0116 0088 0067 0050 0037 0027 0020 0014 0010 0007 0005 0003 0002 0002 0001 | 0,3980 3932 3847 3725 3572 3391 3187 2966 2732 2492 2251 2012 1781 1561 1354 1163 0989 0833 0694 0573 0468 0379 0303 0241 0189 0147 0113 0086 0065 0048 0036 0026 0019 0014 0010 0007 0005 0003 0002 0002 0001 | 0,3977 3925 3836 3712 3555 3372 3166 2943 2709 2468 2227 1989 1758 1539 1334 1145 0973 0818 0681 0562 0459 0371 0297 0235 0184 0143 0110 0084 0063 0047 0035 0025 0018 0013 0009 0007 0005 0003 0002 0001 0001 | 0,3973 3918 3825 3697 3538 3352 3144 2920 2685 2444 2203 1965 1736 1518 1315 1127 0957 0804 0669 0551 0449 0363 0290 0229 0180 0139 0107 0081 0061 0046 0034 0025 0018 0013 0009 0006 0004 0003 0002 0001 0001 |
Приложение 2
Таблица значений функции Лапласа 
, 
|
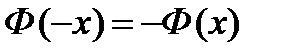
| Сотые доли | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1.4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 | 0,0000 0398 0793 1179 1554 1915 2257 2580 2881 3159 3413 3643 3849 4032 4192 4332 4452 4554 4641 4713 4772 4821 4861 4893 4918 4938 4953 4965 4974 4981 4987 4990 4993 4995 4997 4998 | 0,0040 0438 0832 1217 1591 1950 2291 2611 2910 3186 3437 3665 3869 4049 4207 4345 4463 4564 4649 4719 4778 4826 4864 4896 4920 4940 4955 4966 4975 4982 4987 4991 4993 4995 4997 4998 | 0,0800 0478 0871 1255 1628 1985 2324 2642 2939 3212 3461 3686 3888 4066 4222 4357 4474 4573 4656 4726 4783 4830 4868 4898 4922 4941 4956 4967 4976 4982 4987 4991 4994 4995 4997 4998 | 0,0120 0517 0910 1293 1664 2019 2357 2673 2967 3238 3485 3708 3907 4082 4236 4370 4484 4582 4664 4732 4788 4834 4871 4901 4925 4943 4957 4968 4977 4983 4988 4991 4994 4996 4997 4998 | 0,0160 0557 0948 1331 1700 2054 2389 2703 2995 3261 3508 3729 3925 4099 4251 4382 4495 4591 4671 4738 4793 4838 4875 4904 4927 4945 4959 4969 4977 4984 4988 4992 4994 4996 4997 4998 | 0,0199 0596 0987 1368 1736 2088 2422 2734 3023 3289 3531 3749 3944 4115 4265 4394 4505 4599 4678 4744 4798 4842 4878 4906 4929 4946 4960 4970 4978 4984 4989 4992 4994 4996 4997 4998 | 0,0239 0636 1026 1406 1772 2123 2454 2764 3051 3315 3554 3770 3962 4131 4279 4406 4515 4608 4686 4750 4803 4846 4881 4909 4931 4948 4961 4971 4979 4985 4989 4992 4994 4996 4997 4998 | 0,0279 0675 1064 1443 1808 2157 2486 2794 3078 3340 3577 3790 3980 4147 4292 4418 4525 4616 4693 4756 4808 4805 4884 4911 4932 4949 4962 4972 4979 4985 4989 4992 4995 4996 4997 4998 | 0,0319 0714 1103 1480 1844 2190 2517 2823 3106 3365 3599 3810 3997 4162 4306 4429 4535 4625 4699 4761 4812 4854 4887 4913 4934 4951 4963 4973 4980 4986 4990 4993 4995 4996 4997 4998 | 0,0359 0753 1103 1217 1879 2224 2549 2852 3133 3389 3621 3830 4015 4177 4319 4441 4545 4633 4706 4767 4817 4857 4890 4916 4936 4952 4964 4974 4981 4986 4990 4993 4995 4997 4998 4998 |
Приложение 3
Таблица значений вероятностей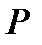 
| Значение
| Число степеней свободы | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | 0,3173 1574 0833 0455 0254 0143 0081 0047 0027 0016 0009 0005 0003 0002 0001 0001 0000 | 0,6065 3679 2231 1353 0821 0498 0302 0183 0111 0067 0041 0025 0015 0009 0006 0003 0002 0001 0001 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 | 0,8013 5724 3916 2615 1718 1116 0719 0460 0293 0186 0117 0074 0046 0029 0018 0011 0007 0004 0003 0002 0001 0001 0000 0000 0000 0000 0000 0000 0000 0000 | 0,9098 7358 5578 4060 2873 1991 1359 0916 0611 0404 0266 0174 0113 0073 0047 0030 0019 0012 0008 0005 0003 0002 0001 0001 0001 0000 0000 0000 0000 0000 | 0,9626 8491 7000 5494 4159 3062 2206 1562 1091 0752 0514 0348 0234 0146 0104 0068 0045 0029 0019 0013 0008 0005 0003 0002 0001 0001 0001 0000 0000 0000 | 0,9856 9197 8088 6767 5438 4232 3208 2381 1736 1247 0884 0620 0430 0296 0203 0138 0093 0062 0042 0028 0018 0012 0008 0005 0003 0002 0001 0001 0001 0000 | 0,9948 9598 8850 7798 6600 5398 4289 3326 2527 1886 1386 1006 0721 0512 0360 0251 0174 0120 0082 0056 0038 0025 0017 0011 0008 0005 0003 0002 0001 0001 | 0,9982 9810 9344 8571 7576 6472 5366 4335 3423 2650 2017 1512 1119 0818 0591 0424 0301 0212 0149 0103 0071 0049 0034 0023 0016 0010 0007 0005 0003 0002 |
