Затухающие колебания осциллятора

ЛЕКЦИЯ № 12

Сложение гармонических колебаний

 

Реальные колебания чаще всего негармонические, носят более сложный характер. Но многие негармонические колебания можно представить в виде суммы гармонических колебаний.

а) сложение однонаправленных гармонических колебаний одинаковой частоты:

 

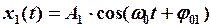    и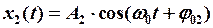 

 

 

Для получения результата воспользуемся методом векторных диаграмм: любое гармоническое колебание графически можно изобразить в виде вращающегося против часовой стрелки вектора длиной, равной амплитуде колебания и имеющего в момент времени t = 0 угол наклона к некоторой оси ОХ, равный начальной фазе этого колебания.

 

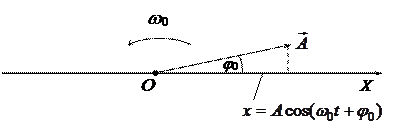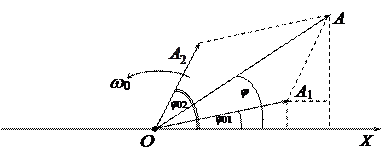Результирующее колебание будет гармоническим:

 

 

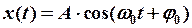
с той же частотой 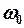, но с новой амплитудой А и новой начальной фазой 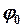, которые можно определить.

(12-1)

б) сложение однонаправленных колебаний с разными частотами:

 

- пусть

 

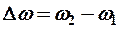
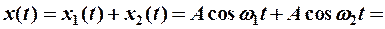
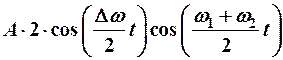
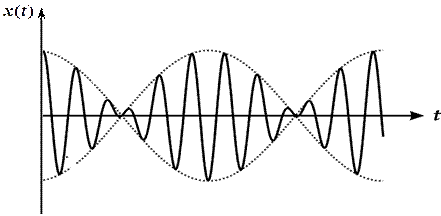
- если 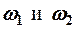  близкие (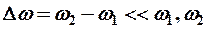), тогда

 

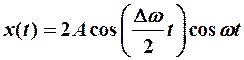                              (12-2)

 

Биения!

 

 

- если 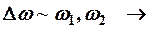   результирующее колебание сложное!

 

в) сложение взаимноперпендикулярных гармонических колебаний одинаковой частоты:

 

     

 

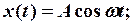
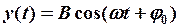
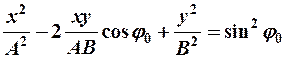                 (12-3)

-         

-     

 

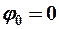
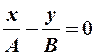
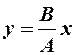
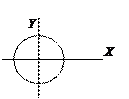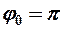
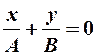
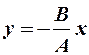
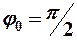
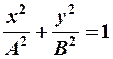-                                                                     A = B = R.

 

г) сложение взаимноперпендикулярных гармонических колебаний с разными частотами:

 

- если частоты кратные друг другу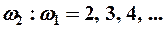

 

- фигуры Лиссажу!

 

- если частоты не кратные        ® сложный негармонический процесс.

Затухающие колебания осциллятора

В реальных условиях присутствует диссипация энергии (, )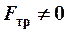

 

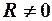механические колебания			электрические колебания

 

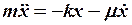
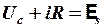
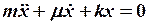
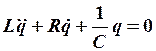
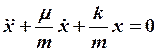
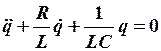
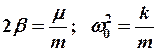
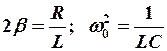
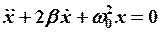                             (12-4)

 

Решением уравнения (12-4) является функция:

 

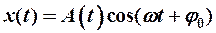                       (12-5)

 

 

 

 

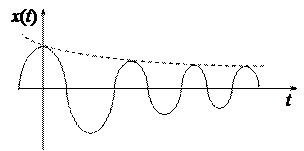
A (t) – амплитуда колебаний уменьшается с течением времени по закону:

 

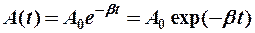                              (12-6)

 

Такие колебания называются затухающими.

b - коэффициент затухания.

 

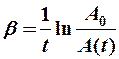                                (2-9а)

 

если 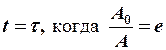  ® 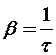.  [ b ] = c^-1.

Коэффициент затухания обратен времени релаксации, т. е. времени, за которое амплитуда колебания уменьшается в «е» раз.

Циклическая (круговая) частота и период затухающих колебаний осциллятора:

 

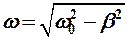
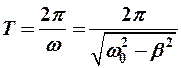                         (12-7)

при 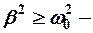апериодический процесс.

 

Второй характеристикой затухающих колебаний является логарифмический декремент затухания – эта скалярная физическая величина, равная натуральному логарифму отношение двух соседних амплитуд, отличающихся по времени на период (предыдущей к последующей):

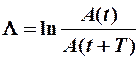                                           (12-8)

 

для 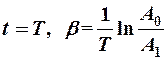®  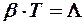                         (12-9)

 

Если 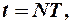тогда

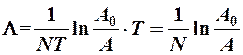                          (12-10)

 

если   ® .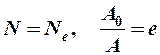

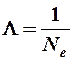Логарифмический декремент затухания обратен количеству полных колебаний, за которые амплитуда уменьшается в «е» раз.

Кроме амплитуды при затухании уменьшается и энергия.

Так как 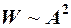, то при затухании

 

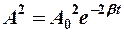
тогда

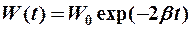                                (12-11)

 

при этом потеря энергии

 

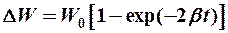                                  (12-12)

С потерями энергии связана третья характеристика затухающих колебаний – добротность – скалярная физическая величина, равная увеличенному в 2 p раз отношению энергии, первоначально запасенной осциллятором, к потерям энергии за один период:

 

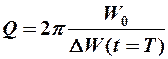,                                     (12-13)

 

при малых затуханиях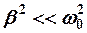

 

 

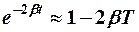
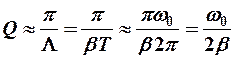.                            (12-14)