V. Дифференцированная самостоятельная работа

ХОД УРОКА

I. Организационная часть.

 

II Актуализация опорных знаний( повторение изученного материала )

 

1. Сформулируйте теорему о сумме углов треугольника.

2. Какой угол называется внешним углом треугольника? Чему равен внешний угол треугольника?

3. Какими могут быть углы в треугольнике?

4. Сформулируйте теорему о соотношениях между сторонами и углами треугольника.

5. Какой треугольник называется прямоугольным? Как называются его стороны, и как их можно сравнить?

6. Сформулируйте признак равнобедренного треугольника.

7. Что такое неравенство треугольника?

8. Какой треугольник называется равнобедренным? Перечислите его свойств

 

Карточка №1	Карточка №2
1. Начертите АВС. Запишите неравенства треугольника. 2. Можно ли из проволоки длиной 15 см согнуть равнобедренный треугольник с основанием 8 см?	1. Сформулируйте признак равнобедренного треугольника. 2. Докажите, что если биссектриса внешнего угла треугольника параллельна стороне треугольника, то треугольник равнобедренный.

 

III. Устная работа на готовых чертежах.

 

1. Какие виды треугольников мы рассматривали на предыдущих уроках?

2. Найдите на рисунке прямоугольный треугольник, назовите его стороны и сравните их.

3. Найдите на рисунке тупоугольный треугольник, сравните его стороны.

4. Найдите остроугольный треугольник. Как можно сравнить стороны такого треугольника, если известны его углы?

 

Дано: CDE, CDE = 66°, CED = 76°, EК – биссектриса.

Доказать: KC > DK.

 

Решение:

1. Так как ЕК – биссектриса, значит, CEK = KED = 38°.

2. DCE = 180° - (66° +76°) = 38°, так как сумма углов треугольника равна 180°.

3. CКE – равнобедренный, так как КCE = СЕК = 38°.

4. В равнобедренном треугольнике равны стороны СК и КЕ.

5. Рассмотрим DKE: КЕ > DK, так как КЕ лежит против большего угла. Значит, КС > DK. Что и требовалось доказать.

 

IV. Решение задачи.

 

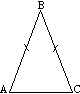
“Периметр равнобедренного треугольника равен 50 см, одна из его сторон на 13 см меньше другой. Найдите стороны треугольника”.

Дано: АВС – равнобедренный, Р_АВС = 50 см,

1 случай: АВ > АС на 13 см,

2 случай: АВ < АС на 13 см.

Найти: АВ, ВС, АС.

Решение:

1 случай

АС = х см, тогда АВ = ВС = (х+13) см. Так как Р_АВС = 50 см, то составим уравнение:

х+х+13+х+13 = 50, х = 8.

АС = 8 см, тогда АВ = 21 см.

8 < 21+21, 21 < 8+21 неравенства треугольника выполняются.

2 случай

АВ = ВС = х см, тогда АС = (х+13) см. Так как Р_АВС = 50 см, то составим уравнение:

х+х+х+13 = 50, х = .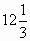

АВ = 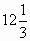см, тогда АС = см.

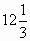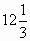> + неравенство треугольника не выполняется, значит, такой треугольник не существует.

Ответ: АС = 8 см, АВ = ВС = 21 см.

V. Дифференцированная самостоятельная работа.

Выбрать вариант самостоятельной работы

I вариант	II вариант
А	A
В треугольнике АВС проведена биссектриса BD. А = 50°, В = 60°. 1) Найдите углы треугольника СВD. 2) Докажите, что BD > DC.	В треугольнике АВС проведена биссектриса BD. АDB = 120°, В = 80°. 1) Найдите углы треугольника СВD. 2) Докажите, что BD > BC.
B	B
В треугольнике MNK проведена биссектриса NO. M = 75°, K = 35°. 1) Докажите, что NOK – равнобедренный. 2) Сравните отрезки MO и ОК.	В треугольнике CDE проведена биссектриса EF. C = 90°, D = 30°. 1) Докажите, что DEF – равнобедренный. 2) Сравните отрезки CF и DF.
C	C
В треугольнике ABC C = 90°, B = 70°. На катете АС отложен отрезок CD, равный СВ. 1) Найдите углы треугольника АВD. 2) Сравните отрезки BD и CD.	В треугольнике ABC C = 90°, B = 70°. На луче СВ отложен отрезок CD, равный СА. 1) Найдите углы треугольника АВD. 2) Сравните отрезки АB и CВ.