2020-05-21
129
1. Определенный интеграл и его непосредственное вычисление.
Пусть функция 
определена на отрезке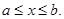 
Разобьем этот отрезок на n частей точками 
выберем на каждом элементарном отрезке 
произвольную точку 
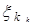и обозначим через 
длину каждого такого отрезка. Интегральной суммой для функции на отрезке 
называется сумма вида
Определение. Определенным интегралом от функции на отрезке называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
Для любой функции непрерывной на отрезке 
всегда существует определенный интеграл 
.
Приведем основные свойства определенного интеграла.
10. Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций:
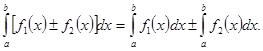
20. Постоянный множитель можно вынести за знак определенного интеграла:
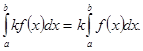
30. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
40. Определенный интеграл с одинаковыми пределами равен нулю:
50. Отрезок интегрирования можно разбить на части:
Для вычисления определенного интеграла от функции в том числе, когда можно найти соответствующий неопределенный интеграл 
служит формула Ньютона-Лейбница:
т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Вычислить следующие определенные интегралы:
Пример 1. 
По формуле Ньютона-Лейбница получаем:
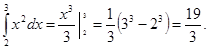
Пример 2. 
Пример 3.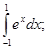 
Пример 4. 
Пример 5. 
Пример 6. 
Пример 7. 
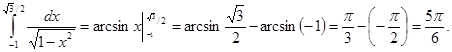
Пример 8.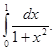 
2. Вычисление определенного интеграла способом подставки.
При вычислении определенного интеграла методом замены переменной (способом подставки) определенный интеграл 
преобразуется с помощью подставки 
или 
в определенный интеграл относительно новой переменной u. При этом старые пределы интегрирования 
и b заменяются соответственно новыми пределами интегрирования α и β, которые находятся из исходной подставки.
Из первой подставки новые пределы интегрирования вычисляются непосредственно: 
Из второй подставки новые пределы интегрирования находятся путем решения уравнений 
и 
относительно 
и 
.
Таким образом, имеем
Вычислить определенные интегралы:
Пример 1. 
Введем новую переменную интегрирования с помощью подстановки 
. Дифференцируя, имеем 
откуда 
Находим новые пределы интегрирования. Подставляя в соотношение значения 
и 
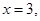соответственно получим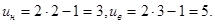 
Следовательно,
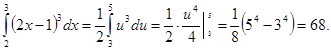
Пример 2. 
Положим 
тогда 
Вычисляем новые пределы интегрирования: 
Поэтому
Пример 3. 
Положим 
тогда 
Вычисляем новые пределы интегрирования: 
Таким образом,
Пример 4. 
Преобразуем подкоренное выражение: 
Положим 
, откуда 
Найдем новые пределы интегрирования: 
Следовательно,
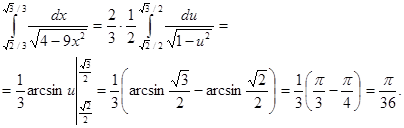
3. Интегрирование по частям в определенном интеграле.
Если функции 
и 
и их производные 
и 
непрерывны в промежутке то формула интегрирования по частям для определенного интеграла имеет вид
Пример 1. Вычислим 
Положим 
тогда 
Следовательно,
