|
I = 
|
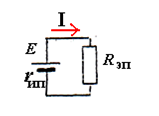
Первый закон Кирхгофа
Алгебраическая сумма токов, входящих в узел электрической цепи, равна алгебраической сумме токов, вытекающих из этого узла.

|

|
Второй закон Кирхгофа
Во всяком замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падения напряжения на электроприёмниках этого контура.

|

|
Расчет простой электрической цепи
Простые электрические цепи рассчитываются методом преобразования, т. е. поэтапным свертыванием и нахождением эквивалентного сопротивления цепи. Для того чтобы рассчитать параметры электрических цепей постоянного тока, необходимо научится описывать схему соединения элементов электрической цепи. Например, если в схеме сопротивление (Рис. 1) R4 и R5 соединены последовательно, то это можно записать R4 пос. R5, если эквивалентное сопротивление R4,5 соединены параллельно R2, то этот вид соединения записывается R4,5 | | R2. Сопротивление R2,4,5 соединены последовательно с R3, сопротивление R2,3,4,5 соединены параллельно R1. Для схемы (Рис. 1) запись будет выглядеть следующим образом: (((R4 пос. R5) | | R2) пос. R3) | | R1.
Метод преобразований
Алгоритм расчета параметров электрической цепи
1.Определяем узлы и ветвиэлектрической цепи.
2.Заменяем группу последовательно соединенных резисторов эквивалентным сопротивлением участка цепи.
3. Заменяем группу параллельно соединенных резисторов эквивалентным сопротивлением участка цепи.
4.Находим эквивалентное сопротивление всей цепи.
5.Определяем силу тока в неразветвленной части цепи.
6.Посредством обратного преобразования находим токи во всех ветвях заданной цепи.
Пример расчёта
1) Расчет эквивалентного сопротивления в цепи
 Рис. 1 Рис. 1
| Задача
| |
 Рис. 2 Рис. 2
| Решение
| |
 Рис. 3
Рис. 3
| 2. Определяем сопротивление резистора R2,4,5.Резисторы R2и R4,5включены параллельно.
R2 * R4,5 7 Ом * 12 Ом
R2,4,5 = ---------------- = ------------------------- = 4,42 Ом
R2 + R4,5 7 Ом + 12 Ом
| |
 Рис. 4
Рис. 4
|
| |
 Рис. 5 Рис. 5
|
|
| 2) Расчет токов в ветвях цепи |
 Рис. 6 Рис. 6
| Решение
1.Указываем направление токов в ветвях.
2.Определяем общий ток I общ в цепи по закону Ома: I общ =  Iобщ =
Iобщ = 
|
| 3. Т.к. к резистору R 1 приложено общее напряжение цепи, определяем силу тока через этот резистор в соответствии с законом Ома: I1 = | |
| 4.В соответствии с 1-м законом Кирхгофа Iобщ = I1+ I3, I3 = Iобщ -- I1, I3 = 35,5A—22A = 13,5A | |
| 5.Потери напряжения на резисторах U1= I1*R1, U1= 22A* 5Ом = 110В. U3 = I3* R3, U3 =13,5A * 6Ом = 81В | |
| 6.По 2-му закону Кирхгофа U1 = U2+U3, U2 = U1 – U3 U2 = 110В – 81В = 29В | |
| 7.По закону Ома I2 = | |
| 8.Падение напряжения на резисторах R2 и R4, R5 одинаковы, так как они включены параллельно U2 = U4,5, U2 = U4,5 = 29В
| |
| 9.Резисторы R4 и R5 включены последовательно, поэтому ток I4 = I5. Рассчитаем силу тока По закону Ома I4 = I5 = | |
 2020-05-21
2020-05-21 92
92

 =
= 
 , I1 =
, I1 = 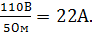
 , I2 =
, I2 =  = 4,14А
= 4,14А , I4 = I5 =
, I4 = I5 = 







