Линии пересечения параллельных плоскостей третьей плоскостью параллельны

Именно поэтому правильный пятиугольник не может быть сечением куба. Ведь 4 из 5 сторон этого пятиугольника лежат в параллельных гранях куба и поэтому параллельны. А у правильного пятиугольника параллельных сторон нет.

2.Теорема о прямой и параллельной ей плоскости:

Пусть прямая m параллельна плоскости α. Если плоскость β проходит через прямую m и пересекает плоскость α по прямой c, то c параллельна m.

Эта теорема помогает, например, при построении сечений пирамиды.

 

Разберем несколько задач на построение сечений.

1. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка М лежит на ребре AD, N — на ребре DC, К — на ребре АВ.

 

 

Проведем МК в плоскости грани ABD и MN в плоскости грани ADC.

Продлим отрезки MN и АС;

Проведем РК в плоскости нижней грани; четырехугольник — искомое сечение.

 

 

 

2. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка N лежит на ребре

 

Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной МК.

Прямая МК параллельна АВ, лежащей в плоскости основания АВС. Значит,

Плоскость сечения проходит прямую МК, параллельную плоскости АВС. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости АВС параллельна прямой МК. Трапеция MKNT — искомое сечение.

 

3. Постройте сечение куба проходящее через вершину 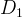и середины ребер и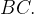

 

Пусть М — середина АВ, N — середина ВС, Продолжим прямую MN до пересечения с продолжениями ребер DC и AD;

Треугольники АМР и KCN — прямоугольные равнобедренные, причем

Проведем — в плоскости задней грани и — в плоскости левой грани куба;

Пятиугольник — искомое сечение. В нем есть параллельные стороны: так как линии пересечения параллельных плоскостей третьей плоскостью параллельны.

 

4. Постройте сечение куба 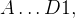проходящее через вершину В и середины ребер и

 

 

Пусть М — середина ребра , N — середина ребра

Поскольку линии пересечения параллельных плоскостей третьей плоскостью параллельны, плоскость сечения пересекает заднюю грань по прямой, параллельной ВМ, а левую грань — по прямой, параллельной BN. Тогда искомое сечение — ромб

 

5. Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, точку М, делящую ребро АS в отношении , и точку N — середину апофемы грани SBC.

 

Пусть SH — апофема грани SBC; N—середина SH.

Проведем MN в плоскости ASH;

Четырехугольник KMEF — искомое сечение.

Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, и точки М и Т — центры граней АSС и SBC.

 

Пусть SЕ и SH — апофемы граней ASC и SBC; точки М и Т делят отрезки SЕ и SH в отношении 2:1, считая от точки S.

Из подобия треугольников SMT и SEH получим, что 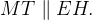Значит

По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и нижней грани параллельна прямой МТ. Это значит, что плоскость сечения пересекает грань АВС по прямой АВ. Достроим сечение.

где — середина ;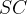

— искомое сечение.

 

6. Постройте сечение куба , проходящее через точку М, лежащую на ребре и точки Т и К, принадлежащие граням АВС и .

 

Точки М и К лежат в плоскости задней грани . Соединив М и К, получим, что

Соединив точки Р и Т в нижней грани, получим FN — линию пересечения плоскости сечения с нижней гранью;

. Трапеция FMEN — искомое сечение.

 

7. И самый сложный случай. Построим сечение куба плоскостью МNK, где , причем расстояния от точек М и N до плоскости АВС различны.

 

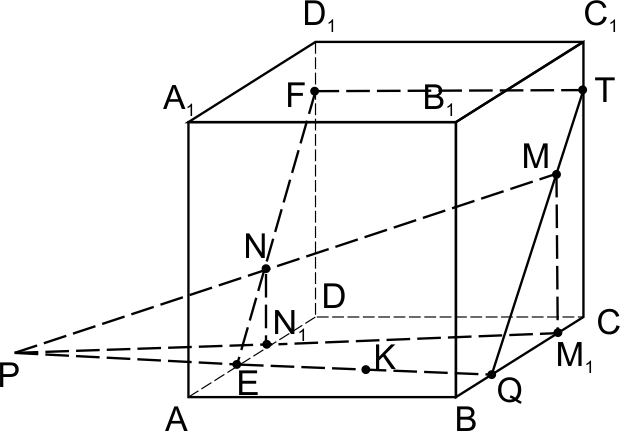
Пусть точк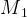и и — проекции точек M и N на плоскость нижней грани

Плоскость проходит через параллельные прямые 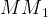и .

Проведем в этой плоскости MN и

.

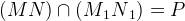Точки Р и К лежат в нижней грани куба, следовательно, плоскость сечения пересекает нижнюю грань по прямой РК. Дальнейшее построение — очевидно.