Отчет по практической работе №1
по дисциплине: «Искусственные нейронные сети и нечеткая логика в задачах контроля и управления»
на тему: «Изучение основных операций над нечеткими множествами»
Вариант №1
Выполнил: студент группы 78-61
ФИО
Проверил: к.т.н., доцент каф. АИТ
Горшкова К. Л.
Альметьевск, 2020
Цель работы: изучить понятие нечеткого множества и основные операций над нечеткими множествами.
Краткие теоретические сведения
Пусть Е – универсальное множество, х – элемент Е, Р – некоторое свойство. Обычное (четкое) множество А универсального множества Е, элементы которого удовлетворяют свойству Р, определяются как множество упорядоченных пар 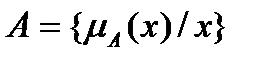 , где
, где  - характеристическая функция, принимающая значение 1, если х удовлетворяет свойству Р, и 0 – в противном случае.
- характеристическая функция, принимающая значение 1, если х удовлетворяет свойству Р, и 0 – в противном случае.
В теории нечетких множеств для элементов х из Е нет однозначного ответа «да/нет» относительно свойства Р. В связи с этим нечеткое множество А универсального множества Е определяется как множество упорядоченных пар с функцией принадлежности  , принимающей значение в некотором упорядоченном множестве М (например, М=[0,1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М называют множеством принадлежностей. Если М={0,1}, то нечеткое подмножество А может рассматриваться как обычное или четкое множество.
, принимающей значение в некотором упорядоченном множестве М (например, М=[0,1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М называют множеством принадлежностей. Если М={0,1}, то нечеткое подмножество А может рассматриваться как обычное или четкое множество.
Основные операции над нечеткими множествами:
1. Включение. Пусть А и B нечеткие множества на универсальном множестве Е. А содержится в B, если 
 . Обозначается
. Обозначается 
2. Равенство. А и В равны, если 
 . Обозначается
. Обозначается 
3. Дополнение. Пусть М=[0,1], А и В дополняют друг друга, если 
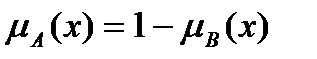 . Обозначается
. Обозначается 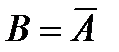 или
или 
4. Пересечение.  - наименьшее нечеткое подмножество, содержащееся одновременно в А и В:
- наименьшее нечеткое подмножество, содержащееся одновременно в А и В: 
5. Объединение.  - наибольшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности
- наибольшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности 
6. Разность.  с функцией принадлежности
с функцией принадлежности 
7. Нечеткие отношения. Нечеткое n-мерное отношение определяется как нечёткое подмножество R на E, принимающее свои значения в М. в случае n =2 и М=[0,1] нечетким отношение R между множествами X=E1 и Y=E2 будет называться функция R: (X,Y)→[0,1], которая ставит в соответствие каждой паре элементов (x,y)  X x Y величину
X x Y величину 
8. Композиция (свертка) двух нечетких отношений. Пусть R1 – нечеткое отношение R1: (X x Y)→[0,1] между X и Y, и R2 – нечеткое отношение R2: (Y x Z)→[0,1] между Y и Z. Нечеткое отношение между X и Z обозначается R1‧R2 и определяется как  , где
, где 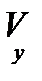 - обозначает операцию выбора наибольшего по y значения называется (max-min)-сверткой отношений R1 и R2.
- обозначает операцию выбора наибольшего по y значения называется (max-min)-сверткой отношений R1 и R2.
Задание:
Пусть на универсальном множестве E заданы нечеткие множества А, В, С:

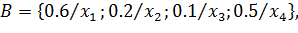

Определить, выполняются ли условия:
1) 
2) 
3) 
4) 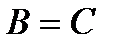
5) 
6) 
7) 
Рассчитать:
1) 
2) 
3) 
4) 
Выполнение работы:
Функции принадлежности:

| 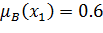
| 
|

| 
| 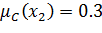
|

| 
| 
|

| 
| 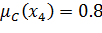
|
Определяем, выполняются ли условия:
1)  - включение. Условие:
- включение. Условие: 


| > | 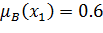
|

| > | 
|

| = | 
|

| < | 
|
Данное условие не выполняется, т.е. А не содержится в B.
2)  - включение. Условие:
- включение. Условие: 

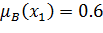
| < | 
|

| < | 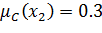
|

| < | 
|

| < | 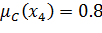
|
Данное условие выполняется, т.е. B содержится в C.
3) 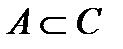 - включение. Условие:
- включение. Условие: 


| > | 
|

| = | 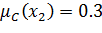
|

| < | 
|

| < | 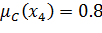
|
Данное условие не выполняется, т.е. A не содержится в C.
4)  - равенство. Условие:
- равенство. Условие: 
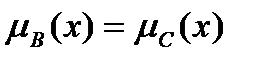
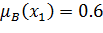
| ≠ | 
|

| ≠ | 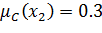
|

| ≠ | 
|

| ≠ | 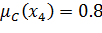
|
Данное условие не выполняется, т.е. B и C не равны.
5)  - дополнение. Условие:
- дополнение. Условие: 
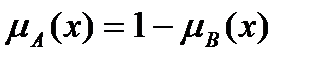

| ≠ | 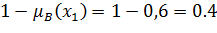
| |

| ≠ | 
| |

| ≠ | 
| |

| ≠ | 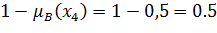
|
Данное условие не выполняется, т.е. A и B не дополняют друг друга.
6)  - дополнение. Условие:
- дополнение. Условие: 


| ≠ | 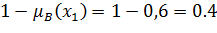
|
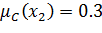
| ≠ | 
|

| ≠ | 
|
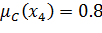
| ≠ | 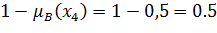
|
Данное условие не выполняется, т.е. C и B не дополняют друг друга.
7)  - дополнение. Условие:
- дополнение. Условие: 


| ≠ | 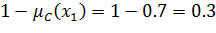
|

| ≠ | 
|

| ≠ | 
|

| = | 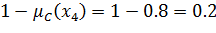
|
Данное условие не выполняется, т.е. A и C не дополняют друг друга
Рассчитаем:
1)  - пересечение, т.е. наибольшее нечеткое подмножество, содержащее одновременно A и B. Функция принадлежности:
- пересечение, т.е. наибольшее нечеткое подмножество, содержащее одновременно A и B. Функция принадлежности: 

| 
| |

| 
| |

| 
| |

| 
|
Таким образом, 
2) 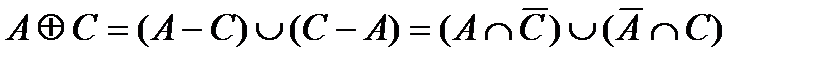 с функцией принадлежности
с функцией принадлежности 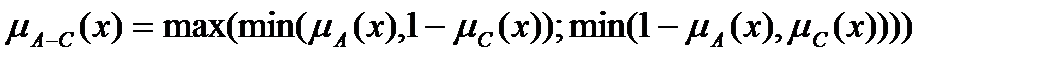

| 
| 
| 
|

| 
| 
| 
|

| 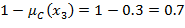
| 
| 
|
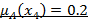
|  0.2 0.2
| 
| 
|
Получаем промежуточную функцию принадлежности:
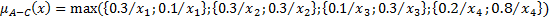
И результат таким образом получается:

3)  с функцией принадлежности
с функцией принадлежности 

| 
| |
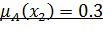
| 
| |

| 
| |

| 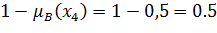
|
Таким образом, 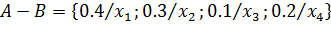
4)  с функцией принадлежности
с функцией принадлежности 
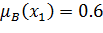
| 
|

| 
|

| 
|

| 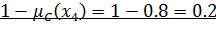
|
Таким образом, 
Вывод: в ходе выполнения данной работы были изучены понятие нечеткого множества и основные операции над нечеткими множествами.
 2020-05-21
2020-05-21 80
80






