Примеры расчета цепей второго порядка

ПРИМЕРЫ РАСЧЕТА ЦЕПЕЙ ВТОРОГО ПОРЯДКА

1.

В;

В;

Ом;

Гн;

Ф.

1)

2)

ПРИМЕРЫ РАСЧЕТА ЦЕПЕЙ ВТОРОГО ПОРЯДКА

1.

В;

В;

Ом;

Гн;

Ф.

1)

2)

 

А

 

 

3)

 

4) При комплексных сопряженных корнях свободная составляющая запишется в виде:

5)

6)

7) В - по исходным данным;

, т.к. в катушке тока не было.

8) Способ I (по законам Кирхгофа)

;

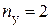
Первый закон Кирхгофа:  уравнение.

Второй закон Кирхгофа: 2 уравнения

 

t= 0

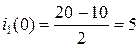А

Таким образом А

Из уравнения 3 системы (**) следует

Вернемся к системе уравнений (*) и продифференцируем уравнения 1 и 2, а затем перепишем их при t= 0.

Имеем 2 уравнения с двумя неизвестными, в результате получим:

Способ II. (схемный метод)

В схеме после коммутации индуктивности заменяем источниками тока с токами из п.э., конденсаторы заменяем на источники ЭДС c напряжениями из п.э.

Получим схему для определения токов в ветвях при t= 0.

, т.е. в ветви  - обрыв, т.е. остался только внешний контур, причем .

По второму закону Кирхгофа имеем:

 

Кроме этого найдем напряжение на источнике тока и ток в ветви с емкостью (всегда).

В нашем случае:

Далее рисуем схему для производных.

В этой схеме, если источники энергии постоянные, то ЭДС закорачивается.

Индуктивность заменяется источником тока с током равным 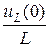, а емкость заменяется источником ЭДС с напряжением .

По ветвям схемы после коммутации «протекают» производные токов.

 

Рассчитываем любым известным способом.

 

По закону Ома:

9)

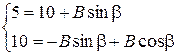
10)

 

А

 

 

3)

 

4) При комплексных сопряженных корнях свободная составляющая запишется в виде:

5)

6)

7) В - по исходным данным;

, т.к. в катушке тока не было.

8) Способ I (по законам Кирхгофа)

;

Первый закон Кирхгофа: 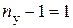 уравнение.

Второй закон Кирхгофа: 2 уравнения

 

t= 0

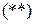
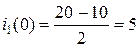А

Таким образом А

Из уравнения 3 системы (**) следует

Вернемся к системе уравнений (*) и продифференцируем уравнения 1 и 2, а затем перепишем их при t= 0.

Имеем 2 уравнения с двумя неизвестными, в результате получим:

Способ II. (схемный метод)

В схеме после коммутации индуктивности заменяем источниками тока с токами из п.э., конденсаторы заменяем на источники ЭДС c напряжениями из п.э.

Получим схему для определения токов в ветвях при t= 0.

, т.е. в ветви  - обрыв, т.е. остался только внешний контур, причем .

По второму закону Кирхгофа имеем:

 

Кроме этого найдем напряжение на источнике тока и ток в ветви с емкостью (всегда).

В нашем случае:

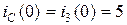
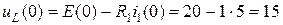
Далее рисуем схему для производных.

В этой схеме, если источники энергии постоянные, то ЭДС закорачивается.

Индуктивность заменяется источником тока с током равным , а емкость заменяется источником ЭДС с напряжением .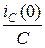

По ветвям схемы после коммутации «протекают» производные токов.

 

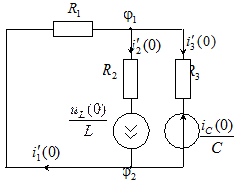
Рассчитываем любым известным способом.

 

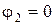
По закону Ома:

9)

10)