Задача урока – продолжить изучение решения тригонометрических неравенств, содержащих функции синус и косинус, перейти от простейших неравенств к более сложным.
Цели урока:
- закрепление знаний тригонометрических формул, табличных значений тригонометрических функций, формул корней тригонометрических уравнений;
- формирование навыка решения простейших тригонометрических неравенств;
- освоение приёмов решения более сложных тригонометрических неравенств;
- развитие логического мышления, смысловой памяти, навыков самостоятельной работы, самопроверки;
- воспитание аккуратности и чёткости в оформлении решения, интереса к предмету, уважения к одноклассникам.
- формирование учебно-познавательных, информационных, коммуникативных компетенций.
Оборудование: графопроектор, раздаточные карточки с готовыми чертежами тригонометрических кругов, переносная доска, карточки с домашним заданием.
Форма организации обучения – урок. Методы обучения, используемые на уроке – словесные, наглядные, репродуктивные, проблемно-поисковые, индивидуального и фронтального опроса, устного и письменного самоконтроля, самостоятельной работы.
развернуть таблицу
| N п/п | Этапы урока | Содержание |
| Организация класса на работу. | ||
| Проверка домашнего задания. | (Сбор тетрадей с домашней работой) | |
| Формулировка цели урока. | – Сегодня на уроке повторим решение простейших тригонометрических неравенств и рассмотрим более сложные случаи. | |
| Устная работа. | (Задания и ответы записаны на кодоскопной ленте, открываю ответы по ходу решения)
 , 2sinx = , 2sinx =  , sin2x = , sin2x =  , sin(x – , sin(x –  ) = 0, cosx = ) = 0, cosx = 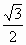 ,
cosx = - ,
cosx = -  , cos2x = 1, tgx = -1. , cos2x = 1, tgx = -1.
| |
| Повторение. | – Вспомним алгоритм решения простейших тригонометрических неравенств.
(На доске – заготовки двух окружностей. Вызываю по одному двух учащихся для решения неравенств.Ученик подробно объясняет алгоритм решения.Класс работает совместно с отвечающими у доски на заранее подготовленных карточках с изображением окружности).
1) sinx  - -  ; ;
 t1< t2;
t1 = arcsin(-
t1< t2;
t1 = arcsin(-  ) = - ) = -  ;
t2 = p + ;
t2 = p + 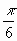 = =  ;
– ;
– 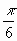 + 2p n + 2p n  х х   + 2p n, n + 2p n, n  Z.
2) cosx Z.
2) cosx  - - 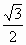 ; ;
 t1> t2;
t1 = arccos(-
t1> t2;
t1 = arccos(- 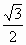 ) = p – arccos ) = p – arccos 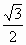 =
= p – =
= p –  = =  ;
t2 = - ;
t2 = -  ;
- ;
-  + 2p n < х < + 2p n < х <  + 2p n, n + 2p n, n  Z.
– Каким образом отражается на ответе решение строгого неравенства?
(3) и 4) неравенства два ученика решают на кодоскопной ленте, класс – самостоятельно на карточках).
3) cosx< Z.
– Каким образом отражается на ответе решение строгого неравенства?
(3) и 4) неравенства два ученика решают на кодоскопной ленте, класс – самостоятельно на карточках).
3) cosx<  ; ;
 t1< t2;
t1 = arccos
t1< t2;
t1 = arccos  = =  ;
t2 = 2p - ;
t2 = 2p -  = =  ; ;
 + 2p n < х< + 2p n < х<  + 2p n, n + 2p n, n  Z.
4) sinx< Z.
4) sinx<  ; ;
 t1> t2;
t1 = arcsin
t1> t2;
t1 = arcsin  = =  ;
t2 = -p - ;
t2 = -p -  = - = -  ; ;
 + 2p n< х< + 2p n< х<  + 2p n, n + 2p n, n  Z.
– Поменяйтесь вариантами, возьмите ручку другого цвета, проверьте работу товарища.
(Самопроверка с кодоскопной ленты. Комментирует решение ученик, выполняющий задание. После возвращения работ – рефлексия).
– Как измениться решение неравенства при замене аргумента х на 2х, на Z.
– Поменяйтесь вариантами, возьмите ручку другого цвета, проверьте работу товарища.
(Самопроверка с кодоскопной ленты. Комментирует решение ученик, выполняющий задание. После возвращения работ – рефлексия).
– Как измениться решение неравенства при замене аргумента х на 2х, на  ? (Оценивание работ учащихся). ? (Оценивание работ учащихся).
| |
| 6. | Новый материал. | – Переходим к более сложным тригонометрическим неравенствам,
решение которых будет сводиться к решению простейших тригонометрических неравенств. Рассмотрим примеры.
(Решение неравенств на доске под руководством учителя).
№1. cos22x – 2cos2x  0.
(Вспомним прием решения тригонометрических уравнений вынесением общего множителя за скобку).
cos2x(cos2x – 2) 0.
(Вспомним прием решения тригонометрических уравнений вынесением общего множителя за скобку).
cos2x(cos2x – 2)  0.
Замена: cos2x = t, 0.
Замена: cos2x = t,   1; t(t – 2) 1; t(t – 2)  0; 0;  Второе неравенство не удовлетворяет условию Второе неравенство не удовлетворяет условию   1.
cos2x 1.
cos2x  0. (Решить неравенство самостоятельно. Проверить ответ).
Ответ: 0. (Решить неравенство самостоятельно. Проверить ответ).
Ответ:  + p n< х< + p n< х<  + p n, n + p n, n  Z.
№2. 6sin2x – 5sinx + 1 Z.
№2. 6sin2x – 5sinx + 1  0.
(Вспомним прием решения тригонометрических уравнений заменой переменной. У доски решает ученик с комментариями).
Замена sinx = t, 0.
(Вспомним прием решения тригонометрических уравнений заменой переменной. У доски решает ученик с комментариями).
Замена sinx = t,   1. 6t2 – 5t +1 1. 6t2 – 5t +1  0, 6(t – 0, 6(t –  )(t – )(t –  ), ), 

 Ответ:
Ответ:  + 2p n + 2p n  х х   + 2p n, -p -arcsin + 2p n, -p -arcsin  + 2p k + 2p k  х х  arcsin arcsin  + 2p k, n, k + 2p k, n, k  Z.
№3. sinx + cos2x> 1.
(Обсуждаем варианты решения. Вспоминаем фомулу косинуса двойного угла. Класс решает самостоятельно, один ученик – на индивидуальной доске с последующей проверкой).
sinx + cos2x – 1> 0, sinx – 2sin2x> 0, sinx(1 – 2sinx) > 0, Z.
№3. sinx + cos2x> 1.
(Обсуждаем варианты решения. Вспоминаем фомулу косинуса двойного угла. Класс решает самостоятельно, один ученик – на индивидуальной доске с последующей проверкой).
sinx + cos2x – 1> 0, sinx – 2sin2x> 0, sinx(1 – 2sinx) > 0, 
 Ответ:
2p n< x<
Ответ:
2p n< x<  + 2p n, + 2p n,  + 2p n< x< p + 2p n, n + 2p n< x< p + 2p n, n  Z.
Проанализировать ситуации, когда ответ к решению квадратного неравенства записываем в виде совокупности двух неравенств, а когда – в виде системы. Полезна следующая схема:
00025165926425165824000000000012516582401
№4. cos Z.
Проанализировать ситуации, когда ответ к решению квадратного неравенства записываем в виде совокупности двух неравенств, а когда – в виде системы. Полезна следующая схема:
00025165926425165824000000000012516582401
№4. cos  cosx – sin cosx – sin  sinx< - sinx< - 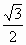 .
(Обсуждение. К доске вызываются по одному ученику на каждый шаг решения, комментируются этапы. Учитель проверяет запись у учеников, работающих на месте).
cos(x + .
(Обсуждение. К доске вызываются по одному ученику на каждый шаг решения, комментируются этапы. Учитель проверяет запись у учеников, работающих на месте).
cos(x +  ) < - ) < - 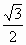 , cost< - , cost< - 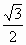 . .

 + 2p n< t< + 2p n< t<  + 2p n, n + 2p n, n  Z, Z,
 + 2p n< x + + 2p n< x +  < <  + 2p n, n + 2p n, n  Z, Z,
 + 2p n< x< + 2p n< x<  + 2p n, n + 2p n, n  Z.
Ответ: Z.
Ответ:
 + 2p n < x < + 2p n < x <  + 2p n, n + 2p n, n  Z.
№5. Определите все а, при каждом из которых неравенство
4sinx + 3cosx Z.
№5. Определите все а, при каждом из которых неравенство
4sinx + 3cosx  а имеет хотя бы одно решение.
(Вспомнить алгоритм решения тригонометрического уравнения с нормирующим множителем. Решение записано на кодоскопной ленте. Открываю его поэтапно по мере рассуждений. Дифференцированная работа).
4sinx + 3cosx а имеет хотя бы одно решение.
(Вспомнить алгоритм решения тригонометрического уравнения с нормирующим множителем. Решение записано на кодоскопной ленте. Открываю его поэтапно по мере рассуждений. Дифференцированная работа).
4sinx + 3cosx  а, М = а, М =  = 5. Разделим обе части неравенства на 5: = 5. Разделим обе части неравенства на 5:  sinx + sinx +  cosx cosx   . Так как ( . Так как ( )2 + ( )2 + ( )2 = 1, то существует такой угол )2 = 1, то существует такой угол  , что cos , что cos  = =  , а sin , а sin  = =  . Перепишем предыдущее неравенство в виде: sin(x + . Перепишем предыдущее неравенство в виде: sin(x +  ) )   . Последнее неравенство, а, значит, и исходное неравенство имеет хотя бы одно решение при каждом а таком, что . Последнее неравенство, а, значит, и исходное неравенство имеет хотя бы одно решение при каждом а таком, что   -1, то есть при каждом а -1, то есть при каждом а  -5. Ответ: а -5. Ответ: а  -5. -5.
|
| 7. | Домашнее задание. | (Раздаю карточки с записью домашнего задания.Комментирую решение каждого неравенства).
|
| 8. | Подведение итогов, рефлексия. | – Назовите приемы решения тригонометрических неравенств. – Каким образом знание алгоритма решения простейших тригонометрических неравенств используется при решении более сложных неравенств? – Какие неравенства вызвали наибольшее затруднение? (Оцениваю работу учащихся на уроке). |
Самостоятельная работа
по результатам освоения материала
Вариант 1
Решите неравенства 1 – 3:
| Вариант 2
Решите неравенства 1 – 3:
|
д/з§37 разобрать примеры 1-4 решить №648(2) и самостоятельную работу по учебнику Ш.А. Алимов 10-11 класс Алгебра и начало математического анализа
 2020-05-21
2020-05-21 171
171 ;
;







