Варианты практической работы

Числовая окружность в координатной плоскости

Поместим окружность в координатную плоскость. По прежнему, каждому числу соответствует точка на окружности. Теперь этой точке на окружности соответствуют две координаты, как и любой точке координатной плоскости.

(рис. 2).

Рис. 2

Наша задача – по данному числу найти не только точку, но и её координаты, и наоборот, по координатам найти одно или несколько соответствующих чисел.

Нахождение прямоугольных координат точек, криволинейные координаты которых кратны

Пример 1.Дана точка – середина дуги Точке соответствуют числа вида

Найти координаты точки (рис. 3).

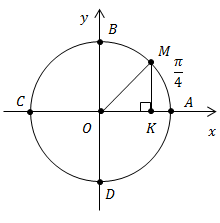
Рис. 3

Решение:

Координаты можно найти двумя разными способами, рассмотрим их по очереди.

1. Точка лежит на окружности, R =1, значит, она удовлетворяет уравнению окружности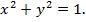

по условию. Мы помним, что величина центрального угла численно равна длине дуги в радианах, значит, угол 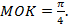Это значит также, что прямая делит первую четверть ровно пополам, значит, это прямая

Точка лежит на прямой поэтому удовлетворяет уравнению этой прямой.

Составим систему из двух уравнений.

Решив систему, получим искомые координаты.

2. Рассмотрим прямоугольный (рис. 4).

Рис. 4

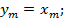
Итак, мы задали число нашли точку и её координаты. Определим также координаты симметричных ей точек (рис. 5).

Рис. 5

Нахождение прямоугольных координат точек, криволинейные координаты которых кратны

Следующая задача – таким же образом определить координаты точек, кратных

Окружность радиуса R =1 помещена в координатную плоскость, Найти точку на окружности и её координаты (рис. 6).

Рис. 6

Решение:

Рассмотрим – прямоугольный.

т. е. угол

Найдем координаты симметричных точек (рис. 7).

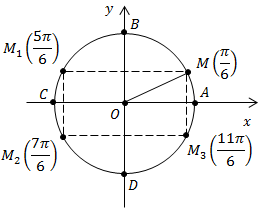
Рис. 7

Мы задали число нашли точку на окружности, эта точка единственная, и нашли её координаты.

Решение задач

 

Пример. Дана точка Найти её прямоугольные координаты.

Решение:

Точка середина третьей четверти (рис. 8).

Рис. 8

Вывод, заключение

Мы поместили числовую окружность в координатную плоскость, научились находить по числу точку на окружности и её координаты. Эта техника лежит в основе определения синуса и косинуса, которые будут рассмотрены далее.

 

 

Домашнее задание

1. Алгебра и начала математического анализа, геометрия. 10 -11классы:учеб. для общеобразовательных организаций: базовый и углубл. уровни /[Ш.А. Алимов и др.] – М.: Просвещение, 2017.

Глава 5, параграф 21, №№ 407-408

 

                        2. ПРАКТИЧЕСКАЯ РАБОТА

ЦЕЛЬ РАБОТЫ:

1. Корректировать знания, умения и навыки в теме: «Тригонометрические функции углов поворота».

2. Закрепить и систематизировать знания по теме.

3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:

1. Ответить на контрольные вопросы:

а) Что такое угол в 1 радиан?

                           б) Как зависят знаки   от того, в какой

координатной четверти расположена точка ? Назовите эти

знаки.                     

2. Изучить условие заданий для практической работы.

3. Оформить отчет о работе.

 

Опорный чертеж

На рисунке совмещены декартова система координат и окружность единичного радиуса. Окружность «эквивалентна» понятию координатной прямой (начало отсчета – точка пересечения окружности с положительной частью оси Ох, положительное направление – против часовой стрелки, единичный отрезок выражен через число ). На окружности отмечены точки, полученные при повороте радиуса окружности, совпадающего с положительной частью оси Ox, на различные углы . Абсциссы этих точек - , ординаты - . Дополнительно проведены две касательные к окружности (линии тангенса и котангенса).

 

ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ

Вариант 1.

1. Выразите величину угла: а) в радианной мере: ; б) в градусной мере:

2. Отметьте на единичной окружности точку . Покажите на чертеже значения  и , если 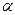 равно .

3. Вычислите: а) ; б) .

Вариант 2.

1. Выразите величину угла: а) в радианной мере: 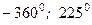; б) в градусной мере: .

2. Отметьте на единичной окружности точку . Покажите на чертеже значения  и , если 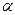 равно .

3. Вычислите: а) 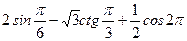; б) .