Радианная мера угла.
Сведения из теории:
Радианная мера
Угол в 1 радиан – это такой центральный угол, длина дуги которого равна радиусу окружности.
Радианная и градусная меры связаны между собой зависимостью1800=π радиан; угол в n 0= 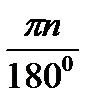 радиан.
радиан.
Значения тригонометрических функций могут быть найдены так, как это делалось в курсе геометрии, из прямоугольного треугольника с гипотенузой равной 1 и по очереди задаваемых углов: 300, 450, 600.
Знаки тригонометрических функций по координатным четвертям:
| Номер координатной четверти | I | II | III | IV |
| sinα | + | + | – | – |
| cosα | + | – | – | + |
| tgα | + | – | + | – |
| ctgα | + | – | + | – |
Единственная четная функция – косинус
cos(- α)= cos α.
Все остальные основные тригонометрические функции нечетные:
sin(- α)= -sin α;
tg(- α)= -tg α;
сtg(- α)= -сtg α.
Таблица 2. Значения основных тригонометрических функций
| Радианная мера угла | 0 | 
| 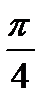
| 
| 
| 
| 
| 
| π |
| Градусная мера угла | 00 | 300 | 450 | 600 | 900 | 1200 | 1350 | 1500 | 1800 |
| sin α | 0 | 
| 
| 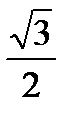
| 1 | 
| 
| 
| 0 |
| cos α | 1 | 
| 
| 
| 0 | 
| 
| 
| -1 |
| tg α | 0 | 
| 1 | 
| – | 
| -1 | 
| 0 |
| ctg α | – | 
| 1 | 
| 0 | 
| -1 | 
| – |
| Радианная мера угла | 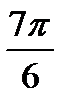
| 
| 
| 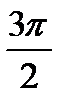
| 
| 
| 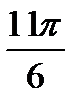
| 2π |
| Градусная мера угла | 2100 | 2250 | 2400 | 2700 | 3000 | 3150 | 3300 | 3600 |
| sin α | 
| 
| 
| -1 | 
| 
| 
| 0 |
| cos α | 
| 
| 
| 0 | 
| 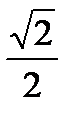
| 
| -1 |
| tg α | 
| 1 | 
| – | 
| -1 | 
| 0 |
| ctg α | 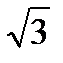
| 1 | 
| 0 | 
| -1 | 
| – |
Пример
Вычислите: sin4050.
Решение:
полный круг – 3600 можно «отбросить»:
sin4050=sin(4050-3600)=sin450=  .
.
Пример
Выразите в радианной мере значение угла 360.
Решение:
чтобы «перевести» градусную меру угла в радианную, необходимо заданное значение умножить на  , т.о. получим
, т.о. получим
360= 
Пример
Выразите в градусной мере значение угла  .
.
Решение:
чтобы «перевести» радианную меру угла в градусную, необходимо заданное значение умножить на  , т. о. получим
, т. о. получим

Задания для самостоятельного решения:
1 вариант
№1. Выразите в радианной (градусной) мере значение угла: 600;  .
№2.Вычислите: .
№2.Вычислите:
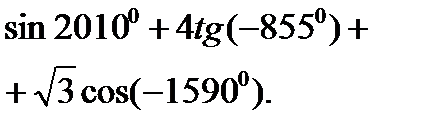
| 2 вариант
№1. Выразите в радианной (градусной) мере значение угла: 1800;  .
№2.Вычислите: .
№2.Вычислите:
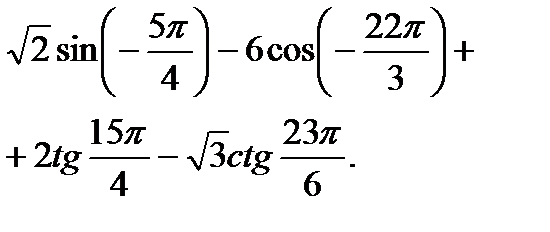
| 3 вариант
№1. Выразите в радианной (градусной) мере значение угла: 2700; 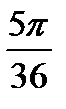 .
№2.Вычислите: .
№2.Вычислите:
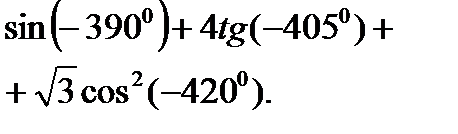
|
Основные тригонометрические тождества.
Сведения из теории:
Основные формулы тригонометрии
Из определений синуса, косинуса, тангенса и котангенса следуют основные тригонометрические тождества:
sin2α+cos2α=1;

tgα∙ctgα=1;

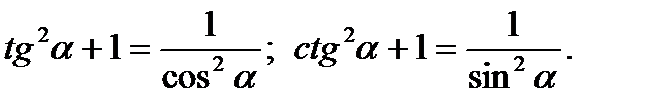
Основой для остальных формул являются формулы сложения:
cos(α-β)=cosαcosβ+sinαsinβ;
cos(α+β)=cosαcosβ-sinαsinβ;
sin(α-β)=sinαcosβ-cosαsinβ;
sin(α+β)=sinαcosβ+cosαsinβ;

Из формул сложения, полагая 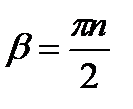 , где n Є Z, получаем формулы приведения преобразования выражений вида:
, где n Є Z, получаем формулы приведения преобразования выражений вида:
sin 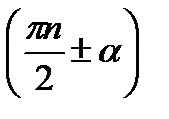 , cos
, cos  , tg
, tg  , ctg
, ctg  , n Є Z.
, n Є Z.
Для запоминания этих формул удобно пользоваться мнемоническим правилом:
1. Перед приведенной функцией ставится тот знак, который имеет исходная функция в соответствующей координатной четверти:
2. Функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс, тангенс).
Пример
Могут ли синус и косинус одного и того же числа быть равными соответственно: 0,4 и 0,7.
Решение:
используя основное тригонометрическое тождество sin2α+cos2α=1, имеем:
0,42+0,72=0,16+0,49=0,65.
Т.к. 0,65≠1 значения синуса и косинуса одного и того же числа не могут быть равными соответственно: 0,4 и 0,7.
Пример
Найдите значения других трех основных тригонометрических функций, если: sinα=-0,8 и π<α<1,5π.
Решение:
используя основное тригонометрическое тождество sin2α+cos2α=1, имеем:
cos2α=1-sin2α, тогда cos2α=1-(-0,8)2=1-0,64=0,36.
Т. к. π<α<1,5π (III координатная четверть), то cosα=-0,6.
По формуле  вычисляем
вычисляем 
По формуле tgα∙ctgα=1 вычисляем ctgα=1׃  =
=  .
.
Задания для самостоятельного решения:
1 вариант
1) Могут ли синус и косинус одного и того же числа быть равными соответственно: 0,5 и 0,5.
2)Найдите значения других трех основных тригонометрических функций, если:
cosα= 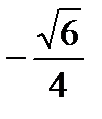 и и  . .
| 2 вариант
1) Могут ли синус и косинус одного и того же числа быть равными соответственно: 0,2 и -0,8.
2)Найдите значения других трех основных тригонометрических функций, если:
sinα= 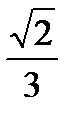 и и  . .
| 3 вариант
1) Могут ли синус и косинус одного и того же числа быть равными соответственно: 0,6 и -0,8.
2)Найдите значения других трех основных тригонометрических функций, если:
cosα= 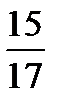 и и  . .
|
 2020-05-25
2020-05-25 223
223






