Решить графическим методом систему уравнений

Урок 27.04.20. алгебра 7

Классная работа

Тема урока: «Решение задач с помощью систем уравнений»

Повторить устно

-Как решить систему способом подстановки?

-Как решить систему способом сложения?

-В чем заключается суть графического способа?

 Работа по теме урока

П.45 стр. 219 – 220 повторить

Задачи записать в тетрадь

Задача № 1

В двух ящиках лежат яблоки. Если из первого ящика переложить во второй 45 яблок, то в обоих ящиках их станет поровну (Рис. 1). Если же из второго ящика переложить в первый 20 яблок, то в первом станет в 3 раза больше яблок, чем во втором (Рис. 2). Сколько яблок лежит в каждом ящике?

Рис. 1. Иллюстрация к задаче 1

Рис. 2. Иллюстрация к задаче 1

Решение

Пусть изначально в первом ящике было яблок, а во втором – яблок. Если из первого ящика переложить во второй 45 яблок, то в обоих ящиках их станет поровну:

Если же из второго ящика переложить в первый яблок, то в первом станет в раза больше яблок, чем во втором: . Запишем полученную систему линейных уравнений: .

Раскроем скобки во втором уравнении: .

В обоих уравнениях выразим через : .

Воспользуемся методом подстановки – подставим выражение во второе уравнение: .

Во втором уравнении перенесем все слагаемые с переменной в левую часть, а без переменной – в правую: .

Найдем – количество яблок во втором ящике: . Подставим найденное значение в первое уравнение и найдем – количество яблок в первом ящике:

Ответ: .

Задача № 2

Один металлический сплав содержит меди, другой – меди (Рис. 3). Сколько килограммов каждого сплава надо взять, чтобы получить 120 кг сплава, содержащего меди (Рис. 4)?

Рис. 3. Иллюстрация к задаче 2

Рис. 4. Иллюстрация к задаче 2

Решение
Пусть необходимо взять кг первого сплава и кг второго сплава. Тогда .

Теперь посчитаем массу меди, она составляет: .

Мы знаем, что – это от чего-то, значит, - это , т.е. от – это 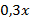.Аналогично от – это , а от – это .

Запишем уравнение: . Запишем полученную систему линейных уравнений: .

В первом уравнении выразим через : .

Воспользуемся методом подстановки – подставим первое уравнение во второе: .

Раскроем скобки во втором уравнении: .

Во втором уравнении оставим слагаемые с переменной в левой части уравнения, а без переменной перенесем в правую: .

Выполним действия: . Найдем – количество кг второго сплава, которое необходимо взять: .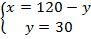

Найдем – количество кг первого сплава: .

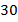Ответ: кг; кг.

Домашнее задание

Повторить §16 п. 45

Решить письменно:

Задание №1

Решить графическим методом систему уравнений

{ 6·(х – 3) = 7у - 1

{ 2·(у + 6) = 3х + 2

Задача №2

Есть два вида сплавов металлов. Первый сплав содержит 12% олова, второй 30%. Сколько килограммов сплава каждого вида надо взять, чтоб получить 180 кг сплава, содержащего 25% олова.