Асимптотическое поведение

 

С полученной выше функцией мы имеем весьма хорошее представление о том, насколько быстр наш алгоритм. Однако нам нет нужды постоянно заниматься таким утомительным занятием, как подсчёт команд в программе. Более того, количество инструкций у конкретного процессора, необходимое для реализации каждого положения из используемого языка программирования, зависит от компилятора этого языка и доступного процессору набора команд. Ранее же мы говорили, что собираемся игнорировать условия такого рода. Поэтому сейчас мы пропустим нашу функцию f через «фильтр» для очищения её от незначительных деталей, на которые теоретики предпочитают не обращать внимания.

Наша функция 6 n + 4 состоит из двух элементов: 6 n и 4. При анализе сложности важность имеет только то, что происходит с функцией подсчёта инструкций при значительном возрастании n. Это совпадает с предыдущей идеей «наихудшего сценария»: нам интересно поведение алгоритма, находящегося в «плохих условиях», когда он вынужден выполнять что-то трудное. Заметьте, что именно это по-настоящему полезно при сравнении алгоритмов. Если один из них побивает другой при большом входном потоке данных, то велика вероятность, что он останется быстрее и на лёгких, маленьких потоках. Вот почему мы отбрасываем те элементы функции, которые при росте n возрастают медленно, и оставляем только те, что растут сильно. Очевидно, что 4 останется 4 вне зависимости от значения n, а 6n наоборот будет расти. Поэтому первое, что мы сделаем, — это отбросим 4 и оставим только f (n) = 6 n.

Имеет смысл думать о 4 просто как о «константе инициализации». Разным языкам программирования для настройки может потребоваться разное время. Например, Java сначала необходимо инициализировать свою виртуальную машину. А поскольку мы договорились игнорировать различия языков программирования, то попросту отбросим это значение.

Второй вещью, на которую можно не обращать внимания, является множитель перед n. Так что наша функция превращается в f (n) = n. Как вы можете заметить, это многое упрощает. Ещё раз, константный множитель имеет смысл отбрасывать, если мы думаем о различиях во времени компиляции разных языков программирования. Поиск в массиве для одного языка программирования может компилироваться совершенно иначе, чем для другого. Например, в Си выполнение A[i] не включает проверку того, что i не выходит за пределы объявленного размера массива, в то время как для Паскаля она существует. Таким образом, данный паскалевский код:

M:= A[ i ]

эквивалентен следующему на Си:

if (i >= 0 && i < n) { M = A[ i ];}

 

Так что имеет смысл ожидать, что различные языки программирования будут подвержены влиянию различных факторов, которые отразятся на подсчёте инструкций. В нашем примере, где мы используем «немой» паскалевский компилятор, игнорирующий возможности оптимизации, требуется по три инструкции на Паскале для каждого доступа к элементу массива вместо одной на Си. Пренебрежение этим фактором идёт в русле игнорирования различий между конкретными языками программирования с сосредоточением на анализе самой идеи алгоритма как таковой.

 

Описанные выше фильтры — «отбрось все факторы» и «оставляй только наибольший элемент» — в совокупности дают то, что мы называем асимптотическим поведением. Для f (n) = 2 n + 8 оно будет описываться функцией f (n) = n. Говоря языком математики, нас интересует предел функции f при n, стремящемся к бесконечности. Если вам не совсем понятно значение этой формальной фразы, то не переживайте — всё, что нужно, вы уже знаете. Строго говоря, в математической постановке мы не могли бы отбрасывать константы в пределе, но для целей теоретической информатики мы поступаем таким образом по причинам, описанным выше. Давайте проработаем пару задач, чтобы до конца вникнуть в эту концепцию.

Найдём асимптотики для следующих примеров, используя принципы отбрасывания константных факторов и оставления только максимально быстро растущего элемента.

Пример 1. f (n) = 5 n + 12 даст f (n) = n. Основания — те же, что были описаны выше.

Пример 2. f (n) = 109 даст f (n) = 1. Мы отбрасываем множитель в 109*1, но 1 по-прежнему нужен, чтобы показать, что функция не равна нулю.

Пример 3. f (n) = n ² + 3 n + 112 даст f (n) = n ². Здесь n ² возрастает быстрее, чем 3 n, который, в свою очередь, растёт быстрее 112.

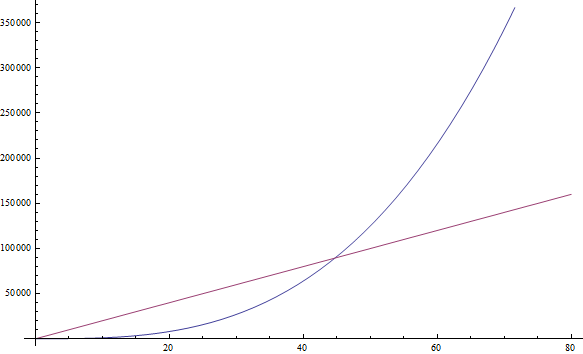
Пример 4. f (n) = n ³ + 1999 n + 1337 даст f (n) = n ³. Несмотря на большую величину множителя перед n, мы по-прежнему полагаем, что можем найти ещё больший n, поэтому f (n) = n ³ всё ещё больше 1999 n (см. рисунок).

 

Пример 5. f (n) = n +  даст f (n) = n, потому что n при увеличении аргумента растёт быстрее, чем .

Упражнение. Определите асимптотическое значение f(n).

1.   f (n) = n ⁶ + 3n

2.   f (n) = 2 ⁿ + 12

3.   f (n) = 3 ⁿ + 2n

4.   f (n) = nⁿ + n

 

 

Сложность

 

Из предыдущей части можно сделать вывод, что если мы сможем отбросить все эти декоративные константы, то говорить об асимптотике функции подсчёта инструкций программы будет очень просто. Фактически, любая программа, не содержащая циклы, имеет f (n) = 1, потому что в этом случае требуется константное число инструкций (конечно, при отсутствии рекурсии — см. далее). Одиночный цикл от 1 до n даёт асимптотику f (n) = n, поскольку до и после цикла выполняет неизменное число команд, а постоянное количество инструкций внутри цикла выполняется n раз.

Руководствоваться подобными соображениями менее утомительно, чем каждый раз считать инструкции, так что давайте рассмотрим несколько примеров на закрепление этого материала.

 

Пример. Следующая программа проверяет, содержится ли в массиве A размера n заданное значение:

ex = false; for (i = 0; i < n; ++i)        { if (A[i ] == v)                    { ex = true; break;                    }        }

 

Такой метод поиска значения внутри массива называется линейным поиском. Это обоснованное название, поскольку программа имеет f (n) = n, то есть является функцией первого порядка (линейной) от n. Инструкция break позволяет программе завершиться раньше, даже после единственной итерации. Однако, напоминаю, что нас интересует самый неблагоприятный сценарий, при котором массив A вообще не содержит заданного значения. Поэтому по-прежнему считаем, что f (n) = n.

Пример. Рассмотрим программу, которая складывает два значения из массива и записывает результат в новую переменную:

v = a[ 0 ] + a[ 1 ]

Здесь у нас постоянное количество инструкций, следовательно, f(n) = 1.

 

Пример. Следующая программа на C++ проверяет, содержит ли вектор (своеобразный массив) A размера n два одинаковых значения:

bool duplicate = false;

for (int i = 0; i < n; ++i) {

for (int j = 0; j < n; ++j) {

   if ((i!= j) && (A[ i ] == A[ j ]))

                {duplicate = true;break;

       }

                           }

if (duplicate) {

   break;

}

}

Два вложенных цикла дадут нам асимптотику вида f (n) = n ².

 

Практическая рекомендация: простые программы можно анализировать с помощью подсчёта в них количества вложенных циклов. Одиночный цикл в n итераций даёт f (n) = n. Цикл внутри цикла — f (n) = n ². Цикл внутри цикла внутри цикла — f (n) = n ³. И так далее.

 

Если в нашей программе в теле цикла вызывается функция, и мы знаем число выполняемых в ней инструкций, то легко определить общее количество команд для программы целиком.

 

Пример. Рассмотрим в качестве примера следующий код на С:

int i;

for (i = 0; i < n; ++i) {

f(n);

}

Если нам известно, что f (n) выполняет ровно n команд, то мы можем сказать, что количество инструкций во всей программе асимптотически приближается к n ², поскольку f (n) вызывается n раз.

 

Практическая рекомендация: если у нас имеется серия из последовательных for-циклов, то асимптотическое поведение программы определяет наиболее медленный из них. Два вложенных цикла, идущие за одиночным, асимптотически тоже самое, что и вложенные циклы сами по себе. Говорят, что вложенные циклы доминируют над одиночными.

 

 

О большое и о малое

 

О большое и о малое – это математические обозначения для сравнения двух функций, означающие следующее:

1) функция f (x) = O (g (x)), если существует константа C > 0, такая, что

 ≤ C∙ ;

2) функция f (x) = o (g (x)), если существует константа ε > 0, при которой  ≤ ε∙  окрестности точки x₀.

 

Так или подобным образом описываются O большое и o малое на математическом языке. По-русски это означает следующее.

1) , например, . Это происходит, когда функции f (x) и g (x) – одного порядка (одного порядка малости).

2) , например, . Это происходит, когда функция f (x) – более высокого порядка (более высокого порядка малости), чем функция g (x).

 

Пример. x ²= o (x) и x ³= o (x), но x = 0,1 << x ² = 0,01

 

O большое и о малое отвечают за сравнение двух бесконечно малых величин, в нашем примере: x ²= o (x), x ³= o (x).

По сути, O большое и o малое (O и o) — математические обозначения для сравнения асимптотического поведения (асимптотики) функций.

Под асимптотикой понимается характер изменения функции при её стремлении к определённой точке.

o (f), «о малое от f» обозначает «бесконечно малое относительно f», пренебрежимо малую величину при рассмотрении f.

Смысл термина «О большое» зависит от его области применения, но всегда O (f) растёт не быстрее, чем f.

 

Историческая справка. Обозначение «O большое» введено немецким математиком Паулем Бахманом во втором томе его книги «Аналитическая теория чисел», вышедшем в 1894 году. Обозначение «о малое» впервые использовано другим немецким математиком, Эдмундом Ландау в 1909 году; с работами последнего связана и популяризация обоих обозначений, в связи с чем их также называют символами Ландау. Обозначение пошло от немецкого слова «Ordnung» (порядок).

 

Фраза «сложность алгоритма есть O (f (n))» означает, что с увеличением параметра n, характеризующего количество входной информации алгоритма, время работы алгоритма будет возрастать не быстрее, чем некоторая константа, умноженная на f (n).

Фраза «функция f (x) является о малым от функции g (x) в окрестности точки p» означает, что с приближением x к p f (x) уменьшается быстрее, чем g (x), то есть отношение | f (x)|/| g (x)| стремится к нулю.

Обычно выражение «f является О большим от g» записывается с помощью равенства f (x) = O (g (x)).

Обычно выражение «f является о малым от g» записывается с помощью равенства f (x) = о (g (x)).

Такие обозначения очень удобны, но требуют некоторой осторожности при использовании. Дело в том, что f (x) = O (g (x)) и f (x) = о (g (x)) не являются равенствами в обычном смысле, представляют собой несимметричные отношения.

В частности, можно писать

f (x) = O (g (x)) или f (x) = о (g (x)),

но выражения

O (g (x)) = f (x) или = о (g (x)) = f (x)

бессмысленны.

Пример. При x à0 верно, что О (х ²) = о (х),

но неверно, что о (х) = О (х ²).

 

При любом х верно, что

о (х) = О (х),

то есть бесконечно малая величина является ограниченной, но неверно, что ограниченная величина является бесконечно малой: О (х) = о (х).

Вместо знака равенства методологически правильнее было бы употребить знаки принадлежности и включения, понимая О () и о () как обозначения для множества функций, то есть используя запись в форме:

х ³ + х ² 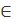О (х ³)

или

О (х ²)   о (х)

вместо соответственно

х ³ + х ² = О (х ³)

и

О (х ²) = о (х).

Однако на практике такая запись встречается крайне редко, в основном, в простейших случаях.

При использовании данных обозначений должно быть явно оговорено (или очевидно из контекста), о каких окрестностях (одно- или двусторонних; содержащих целые, вещественные, комплексные или другие числа) и о каких допустимых множествах функций идет речь (поскольку такие же обозначения употребляются и применительно к функциям многих переменных, к функциям комплексной переменной, к матрицам и др.).