Домашнее задание: повторить определения и свойства окружности, решить задачи

Тема урока: Окружность и круг

1. Что такое окружность?

Пример неверного ответа на вопрос, что такое окружность. Окружностью называется множество точек плоскости, равноудаленных от одной точки, называемой центром.

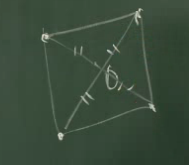
Если рассмотреть квадрат и его вершины, то вершины квадрата будут равноудалены от центра квадрата. Но это не есть окружность.

Определение:

Окружностью называется множество всех точек плоскости, равноудаленных от одной точки, называемой центром.

Это также означает, что если точка A лежит на окружности, то расстояние OA = R, где R – радиус окружности.

Обратно, если для некоторой точки B расстояние OB = R, то точка B лежит на окружности.

2. Взаимное расположение окружности и прямой

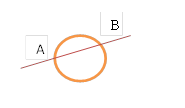
Прямая не пересекается с окружностью	Прямая пересекает окружность в одной точке – такая прямая называется касательной	Прямая пересекает окружность в двух точках
	Свойство: прямая является касательной к окружности, когда радиус, проведенный в точку касания, перпендикулярен прямой	Центр окружности лежит на серединном перпендикуляре к отрезку AB

 

3. Точка на окружности. Теорема о вписанном угле. Следствия

Из точки на окружности можно провести либо 1 касательную, либо 2 хорды.

Рассмотрим угол, который образован точкой на окружности и двумя хордами, продолжения которых пересекают эту окружность.

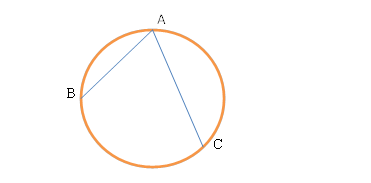
Получили вписанный треугольник ABC.

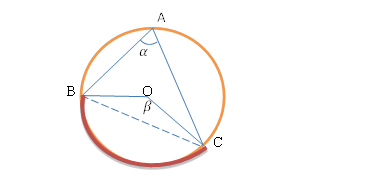
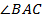называется вписанным в окружность. Ему соответствует центральный угол .

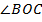Эти углы опираются на дугу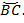

Дугу можно измерить угловым измерением, а также можно измерить длину дуги.

Угловое измерение: =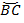

 

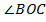
Теорема 1:

Вписанный угол измеряется половиной дуги, на которую он опирается.

=

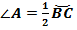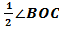
Идея доказательства:

Разобьем угол 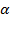на 2 угла: 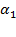и .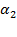

OA = OB = R 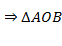– равнобедренный.

Т.е. ∠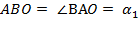

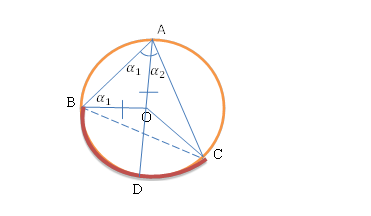
Внешний угол равен сумме двух внутренних не смежных с ним углов треугольника 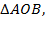т.е.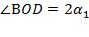

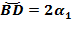
Аналогично,

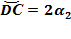
Суммируя дуги,

=

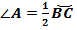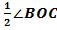
Следствие 1

Вписанные углы, опирающиеся на одну дугу, равны.

Следствие 2

Любой вписанный угол, опирающийся на диаметр, прямой.

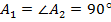∠ ∠ (так как они опираются на центральный развернутый угол, который равен 180 ).

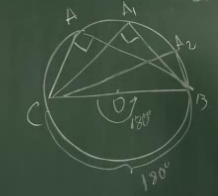
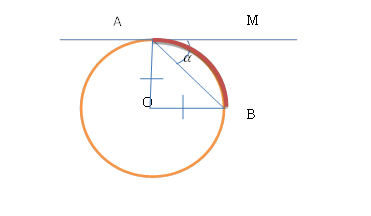
4. Точка на окружности. Угол между касательной и хордой

Угол между касательной и хордой измеряется половиной дуги, на которую он опирается, и равен любому вписанному углу, опирающемуся на эту дугу.

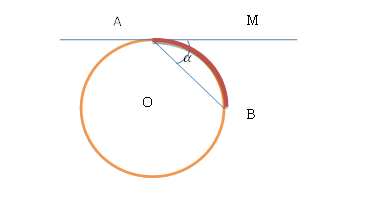
Дано: AM – касательная, ∠MAB =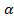

Доказать: 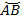= = 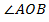2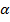

Доказательство:

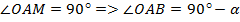
Т.к. 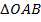равнобедренный,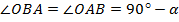

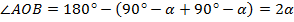
5. Задачи

Задача

Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиеся в точке С. Найдите угол АСВ.

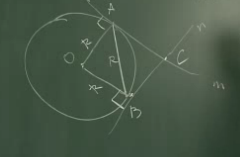
Дано: 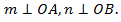Найти: ∠ACB.

Решение:

1. OA = OB = R => 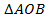равносторонний. => ∠AOB = 60

2. Рассмотрим четырехугольник ACBO. Сумма углов в четырехугольнике равна 360 .

∠ACB = 360 – (90 + 90 + 60 ) = 120 .

Ответ: 120

Задача

Через точку А окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними.

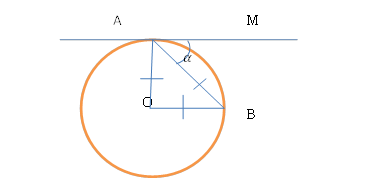
Решение:

1. OA = OB = R => 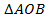равносторонний. => ∠OAB = 60

2. ∠BAM = 90 – 60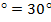

Ответ: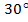

 

Домашнее задание: повторить определения и свойства окружности, решить задачи

1. Из точки А к окружности радиуса 6 см проведена касательная длиной 8 см.

 Найти расстояние от точки А до центра этой окружности.

 2.Из точки М к окружности с центром в точке О проведена касательная,расстояние от точки М до точки касания равно 12 см. Найти радиус этой окружности, если расстояние от точки М до центра этой окружности равно

15 см.

 3.Вычислить площадь кругового сектора, если радиус круга равен 6 м,а соответствующий центральный угол равен 60 градусов.

 4.Медиана равностороннего треугольника равна 18 см. Найти радиус описанной окружности около этого треугольника.

 5.Около равнобедренного треугольника с основанием 20 см и углом при основании 75 градусов описана окружность. Найти радиус этой окружности.