Решение типичных примеров

Задание для 101 группы по алгебре за 28 апреля

Тема  «Зависимость между синусом и косинусом одного и того же угла»

1. Посмотри видео урок по теме Тема  «Зависимость между синусом и косинусом одного и того же угла»  по ссылке  videouroki.net

Теоретический материал для самостоятельного изучения

Рассмотрим точку В(х;у), лежащую на тригонометрической окружности. Она получена поворотом точки А(1;0) вокруг начала координат на угол .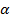

Синусом угла 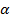является ордината точки В(х;у). Косинусом угла 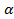является её абсцисса.

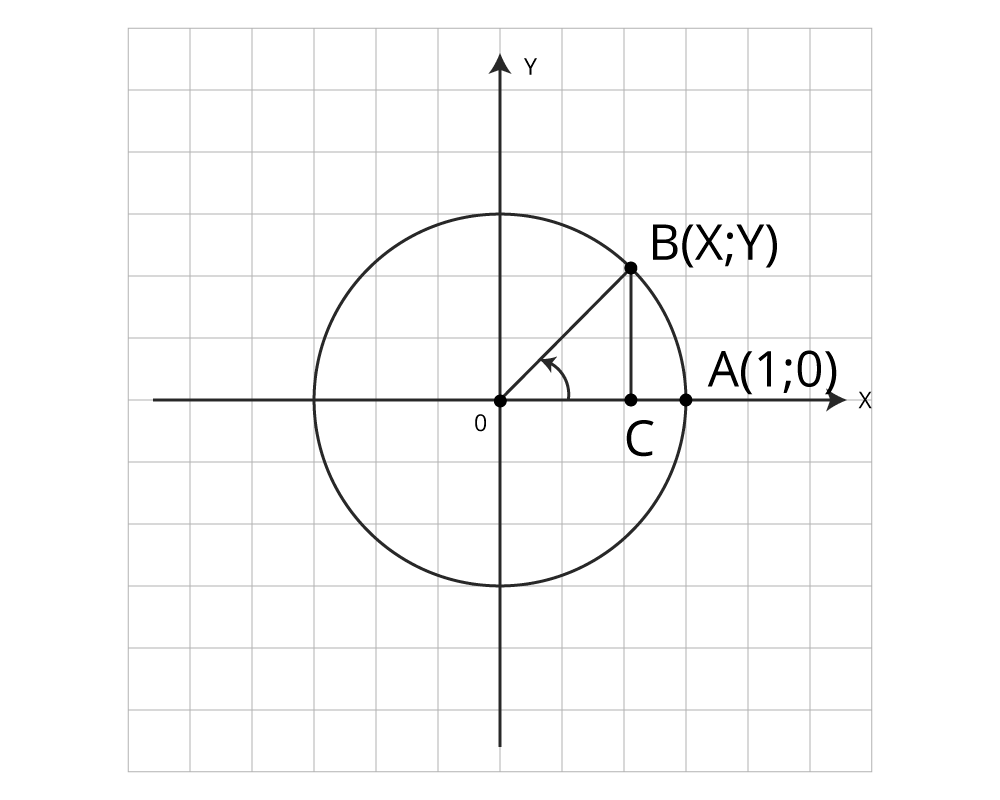
Рисунок 1 – точка В на тригонометрической окружности

Образовался прямоугольный треугольник ОВС. По теореме Пифагора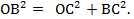

Катет ОС - это абсцисса точки В или 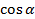, катет ВС- её ордината, или 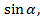а гипотенуза ОВ - радиус единичной окружности, ОВ=1.Получаем формулу:

(1)

В тригонометрии её называют основным тригонометрическим тождеством. Она связывает синус с косинусом. А это значит, чо зная значения синуса, можно найти значения косинуса и наоборот.

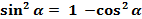
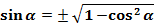(2)

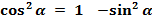
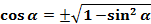(3)

В этих равенствах знаки перед корнем определяются по знакам синуса и косинуса.

Решение типичных примеров

Пример 1. Найти 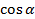, если , .

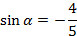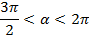Выясним знак косинуса. Из условия опрелеляем, что угол 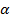в 4 четверти,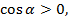

Подставим значение 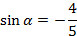в формулу (3), получаем:

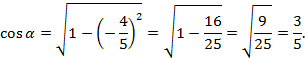
Ответ: .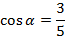

Пример 2. Могут ли одновременно выполняться равенства 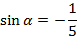и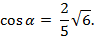

Чтобы одновременно выполнялись эти равенства, необходимо выполнение условия

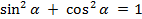. Подставим данные значения в формулу и проверим верно ли равенство:.

;

;

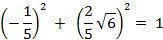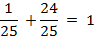1=1, верно.

Ответ: данные равенства могут выполняться одновременно.

А какая же зависимость между тангенсом и котангенсом одного угла?

По определению: , .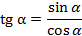

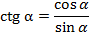Перемножим эти равенства и получим формулу, которая связывает тангенс и котангенс:

.

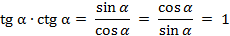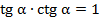, (4)

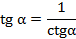и ,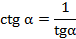

причём угол 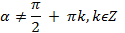и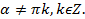

Из этих формул видно, что тангенс и котангенс являются взаимнообратными числами.

Если 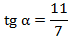, то .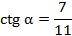

Пример. Могут ли одновременно выполняться равенства 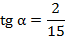и 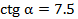? Подставляем данные значения в формулу (4) и получаем верное равенство.

.

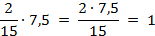Ответ: данные равенства могут выполняться одновременно.

Пример. Известно, что 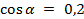; 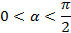. Найт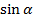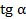и , и .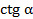

Угол 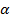в первой четверти, значит все значения положительны. Найдём их по тригонометрическим формулам.

1. ;
2. ;
3. .

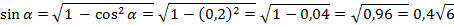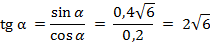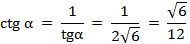Применяя тригонометрические формулы, можно зная одно из чисел 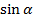, , 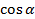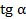и 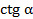, найти остальные три. Эти формулы являются тождествами.

Домашнее задание

§25, №456, 457(1;3).