Урок 3
Тема урока: «Линейные уравнения и их решение».
Проверяем домашнее задание
№ 334 (б, г)
б) 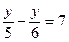 ;
6 у – 5 у = 210;
у = 210
Ответ: {210}
г) 4,7 t – 3,8 = 0,3 t – 0,7 t – 7,2 + 3,4 t;
4,7 t – 0,3 t + 0,7 t − 3,4 t = – 7,2 + 3,8;
1,7 t = − 3,4;
t = − 2
Ответ: {− 2} ;
6 у – 5 у = 210;
у = 210
Ответ: {210}
г) 4,7 t – 3,8 = 0,3 t – 0,7 t – 7,2 + 3,4 t;
4,7 t – 0,3 t + 0,7 t − 3,4 t = – 7,2 + 3,8;
1,7 t = − 3,4;
t = − 2
Ответ: {− 2}
|
| № 335 (в, г) в) z (z – 3) = (4 + z)(z – 5); z 2 – 3 z = 4 z + z 2 – 20 – 5 z; z 2 – 3 z − 4 z − z 2 + 5 z = − 20; − 2 z = − 20; z = 10 Ответ: {10} г) (a + 8)(1 – a) = 8 – a (a – 11); а + 8 – а 2 – 8 а = 8 – а 2 + 11 а; а – а 2 – 8 а + а 2 − 11 а = 8 – 8; − 18 а = 0; а = 0 Ответ: {0} |
№ 338 (а, б)
а) 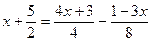 ;
8 х + 20 = 8 х + 6 – 1 + 3 х;
8 х – 8 х – 3 х = 6 – 1 – 20;
− 3 х = − 15;
х = 5
Ответ: {5}
б) ;
8 х + 20 = 8 х + 6 – 1 + 3 х;
8 х – 8 х – 3 х = 6 – 1 – 20;
− 3 х = − 15;
х = 5
Ответ: {5}
б) 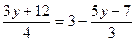 ;
9 у + 36 = 36 – 20 у + 28;
9 у + 20 у = 36 + 28 – 36;
29 у = 28;
у = ;
9 у + 36 = 36 – 20 у + 28;
9 у + 20 у = 36 + 28 – 36;
29 у = 28;
у = 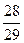 Ответ: {
Ответ: { 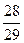 } }
|
2) самостоятельная работа № 1:
1. Решите уравнение: 4(2 t – 5) – 9 t = 3(6 – 4 t) + 10 t.
2. При каких значениях переменной значение выражения 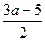 равно значению выражения равно значению выражения 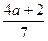 .
3. Найдите корни уравнения: .
3. Найдите корни уравнения: 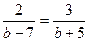 .
4*. Равносильны ли уравнения: .
4*. Равносильны ли уравнения: 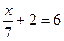 и 3,4 у + 7,9 у = 12,3 у + 39,2 – 2,4 у.
5*. Какое число можно подставить вместо p, чтобы корнем уравнения было четное число: и 3,4 у + 7,9 у = 12,3 у + 39,2 – 2,4 у.
5*. Какое число можно подставить вместо p, чтобы корнем уравнения было четное число: 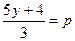 . .
|
3) самостоятельная работа № 2:
1. Решите уравнение: 5(3 x – 8) – 8 x = 4(2 + 9 x) − 30 x.
2. При каких значениях переменной значение выражения 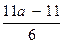 равно значению выражения равно значению выражения 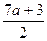 .
3. Найдите корни уравнения: .
3. Найдите корни уравнения: 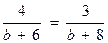 . .
|
Проверяем себя красной ручкой с исправлением ошибок.
Оценку ставим по желанию.
образец выполнения самостоятельной работы № 1:
| 1. Ответ: {38} 2. Ответ: {3} 3. Ответ: {31} |
эталон для самопроверки самостоятельной работы № 1:
| 1. 4(2t – 5) – 9t = 3(6 – 4t) + 10t; 8t – 20 – 9t = 18 – 12t + 10t; – 20 – t = 18 – 2t; – t + 2t = 18 + 20; t = 38 Ответ: {38} |
Раскрыть скобки, применяя распределительное свойство умножения.
Упростить левую часть и правую часть уравнения.
Перенести все неизвестные слагаемые в левую часть уравнения, а известные – в правую, меняя знаки переносимых слагаемых на противоположные знаки.
Упростить левую часть и правую часть уравнения.
Записать линейное уравнение в виде kх = с, где k, с Î Q
k ¹ 0, единственный корень 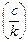
|
2.
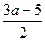 = = 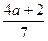 ;
7(3а – 5) = 2(4а +2);
21а – 35 = 8а + 4;
21а – 8а = 35 + 4;
13а = 39;
а = 39: 13;
а = 3
Ответ: {3} ;
7(3а – 5) = 2(4а +2);
21а – 35 = 8а + 4;
21а – 8а = 35 + 4;
13а = 39;
а = 39: 13;
а = 3
Ответ: {3}
|
Применить основное свойство пропорции.
Раскрыть скобки, применяя распределительное свойство умножения.
Перенести все неизвестные слагаемые в левую часть уравнения, а известные – в правую, меняя знаки переносимых слагаемых на противоположные знаки.
Упростить левую часть и правую часть уравнения.
Записать линейное уравнение в виде kх = с, где k, с Î Q
k ¹ 0, единственный корень 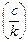
|
3.
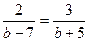 ;
2(b + 5) = 3(b – 7);
2b + 10 = 3b – 21;
2b – 3b = − 21 – 10;
− b = − 31;
b = 31
Ответ: {31} ;
2(b + 5) = 3(b – 7);
2b + 10 = 3b – 21;
2b – 3b = − 21 – 10;
− b = − 31;
b = 31
Ответ: {31}
|
Применить основное свойство пропорции.
Раскрыть скобки, применяя распределительное свойство умножения.
Перенести все неизвестные слагаемые в левую часть уравнения, а известные – в правую, меняя знаки переносимых слагаемых на противоположные знаки.
Упростить левую часть и правую часть уравнения.
Записать линейное уравнение в виде kх = с, где k, с Î Q
k ¹ 0, единственный корень 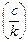
|
эталон для самопроверки самостоятельной работы № 2:
| 1. 5(3x – 8) – 8x = 4(2 + 9x) − 30x; 15х – 40 – 8х = 8 + 36х − 30х; 7х – 40 = 8 + 6х; 7х − 6х = 8 + 40; х = 48; Ответ: {48} |
Раскрыть скобки, применяя распределительное свойство умножения.
Упростить левую часть и правую часть уравнения.
Перенести все неизвестные слагаемые в левую часть уравнения, а известные – в правую, меняя знаки переносимых слагаемых на противоположные знаки.
Упростить левую часть и правую часть уравнения.
Записать линейное уравнение в виде kх = с, где k, с Î Q k ¹ 0, единственный корень 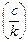
|
| 2.
2(11а – 11) = 6(7а + 3); Первый способ: Второй способ: 22а – 22 = 42а + 18; 11а – 11 = 3(7а + 3); 22а – 42а = 18 + 22; 11а – 11 = 21а + 9; − 20а = 40 11а – 21а = 9 + 11; а = 40: (− 20); − 10а = 20; а = − 2 а = 20: (− 10); а = − 2 Ответ: {− 2} |
Применить основное свойство пропорции. | |
| Первый способ | Второй способ | |
Раскрыть скобки, применяя распределительное свойство умножения.
Перенести все неизвестные слагаемые в левую часть уравнения, а известные – в правую, меняя знаки переносимых слагаемых на противоположные знаки.
Упростить левую часть и правую часть уравнения.
Записать линейное уравнение в виде kх = с, где k, с Î Q
k ¹ 0, единственный корень 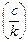
| Разделить обе части уравнения на 2.
Раскрыть скобки, применяя распределительное свойство умножения.
Перенести все неизвестные слагаемые в левую часть уравнения, а известные – в правую, меняя знаки переносимых слагаемых на противоположные знаки.
Упростить левую часть и правую часть уравнения.
Записать линейное уравнение в виде kх = с, где k, с Î Q
k ¹ 0, единственный корень 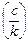
| |
3.
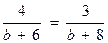 ;
4(b + 8) = 3(b + 6);
4b + 32 = 3b + 18;
4b – 3b = 18 – 32;
b = − 14;
Ответ: {− 14} ;
4(b + 8) = 3(b + 6);
4b + 32 = 3b + 18;
4b – 3b = 18 – 32;
b = − 14;
Ответ: {− 14}
|
Применить основное свойство пропорции. Раскрыть скобки, применяя распределительное свойство умножения. Перенести все неизвестные слагаемые в левую часть уравнения, а известные – в правую, меняя знаки переносимых слагаемых на противоположные знаки. Упростить левую часть и правую часть уравнения. Записать линейное уравнение в виде kх = с, где k, с Î Q k ¹ 0, единственный корень | |
подробный образец выполнения дополнительных заданий:
4*. 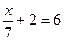 3,4у + 7,9у = 12,3у + 39,2 – 2,4у. 3,4у + 7,9у = 12,3у + 39,2 – 2,4у.
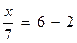 ; 11,3у = 9,9у + 39,2; ; 11,3у = 9,9у + 39,2;
 ; 11,3у − 9,9у = 39,2;
х = 28 1,4у = 39,2;
у = 39,2: 1,4;
у = 28
Ответ: уравнения равносильны ; 11,3у − 9,9у = 39,2;
х = 28 1,4у = 39,2;
у = 39,2: 1,4;
у = 28
Ответ: уравнения равносильны
|
5*. 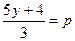 .
5у + 4 = 3р;
5у = − 4 + 3р;
у = − 0,8 + 0,6р
Ответ: р – любое число. .
5у + 4 = 3р;
5у = − 4 + 3р;
у = − 0,8 + 0,6р
Ответ: р – любое число.
|
Домашнее задание:
| № 306; 310 (в,г), 322 (е), 319 (а). |
 2020-05-21
2020-05-21 116
116






