1. Определение при помощи тригонометрических операций основных тригонометрических функций y=sinx, y=cosx и y=tgx, y=ctgx
2. Область определения и значения, периодичность, обращение в нуль, сохранение знака, наибольшие и наименьшие значения, промежутки монотонности
Вопрос 1. Определение при помощи тригонометрических операций основных тригонометрических функций y=sinx, y=cosx и y=tgx, y=ctgx
Любому действительному числу  соответствует единственная точка на единичной окружности
соответствует единственная точка на единичной окружности  У точки
У точки  есть единственная ордината, которая и называется синусом числа
есть единственная ордината, которая и называется синусом числа  (рис. 1).
(рис. 1).




Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что  т.к.
т.к.  это ордината точки единичной окружности.
это ордината точки единичной окружности.
Рассмотрим график функции  . Вспомним геометрическую интерпретацию аргумента. Аргумент – это центральный угол, измеряемый в радианах. По оси
. Вспомним геометрическую интерпретацию аргумента. Аргумент – это центральный угол, измеряемый в радианах. По оси  мы будем откладывать действительные числа или углы в радианах, по оси
мы будем откладывать действительные числа или углы в радианах, по оси  соответствующие значения функции.
соответствующие значения функции.
|
|
|
Например, угол  на единичной окружности соответствует точке
на единичной окружности соответствует точке  на графике (рис. 2)
на графике (рис. 2)
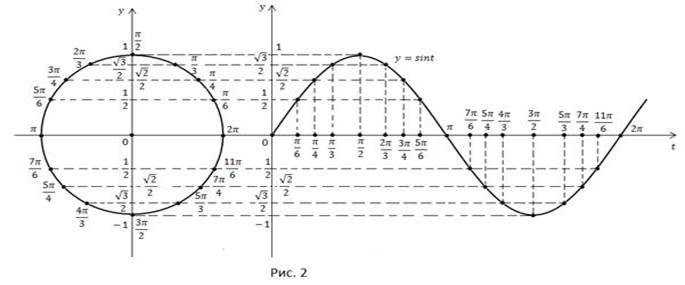
График функции  можно получить по формулам приведения
можно получить по формулам приведения  поэтому график косинуса – это синусоида, сдвинутая по оси x на
поэтому график косинуса – это синусоида, сдвинутая по оси x на  влево.
влево.
Вопрос 2. Область определения и значения, периодичность, обращение в нуль, сохранение знака, наибольшие и наименьшие значения, промежутки монотонности.
Свойства и графики тригонометрических функций y = sinx
а) Область определения: D (y) = (-∞;+∞)
б) Область значений: E (y) = [ – 1, 1 ].
в) Четность, нечетность: функция нечетная.
г ) Периодичность: функция периодическая с основным периодом T = 2π
д) Нули функции: sin x = 0 при x = π n, n  Z.
Z.
е) Промежутки знакопостоянства:
 ;
;  .
.
ж) Промежутки монотонности:
 ;
;
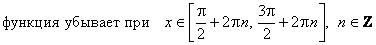 .
.
з) Экстремумы:
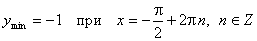 ;
;  .
.
График функции y = sin x

Свойства и графики тригонометрических функций y = cosx
а) Область определения: D (y) = (-∞;+∞)
б) Область значений: E (y) = [ – 1, 1 ].
в) Четность, нечетность: функция четная.
г ) Периодичность: функция периодическая с основным периодом T = 2 π
д) Нули функции: cos x = 0 при x =  + π n, n
+ π n, n  Z.
Z.
е) Промежутки знакопостоянства:
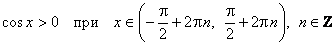 ;
;
 .
.
.ж) Промежутки монотонности:
 ;
;
 .
.
з) Экстремумы:
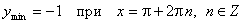 ;
;  .
.
График функции y = cos x

Свойства и графики тригонометрических функций y = tgx
а) Область определения: D (у) = (-∞;+∞)\ {  /2 +
/2 +  n (n
n (n  Z) }.
Z) }.
б) Область значений: E (у) = (-∞;+∞)
в) Четность, нечетность: функция нечетная.
г ) Периодичность: функция периодическая с основным периодом T = π.
д) Нули функции: tg x = 0 при x = π n, n  Z.
Z.
е) Промежутки знакопостоянства:
 ;
;  .
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
|
|
|
з) Экстремумы: нет.
График функции y = tg x

Свойства и графики тригонометрических функций y = ctgx
а) Область определения: D (у) = (-∞;+∞)\ {  n (n
n (n  Z) }.
Z) }.
б) Область значений: E (у) = (-∞;+∞)
в) Четность, нечетность: функция нечетная.
г ) Периодичность: функция периодическая с основным периодом T = π.
д) Нули функции: ctg x = 0 при x = π /2 + π n, n  Z.
Z.
е) Промежутки знакопостоянства;
 ;
;  .
.
ж) Промежутки монотонности: функция убывает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
График функции y = ctg x

 2020-05-25
2020-05-25 116
116






