Соответствие между возможными значениями дискретной случайной величины и их вероятностями называется законом распределения этой величины

Для дискретных и непрерывных случайных величин закон распределения задается по-разному.

Обозначим возможные значения случайной величины Х через х_i, а соответствующие им вероятности через р_i. Тогда закон распределения дискретной случайной величины можно задать следующими способами:

1. В виде таблицы, которая называется рядом распределения:

Таблица 1.1. Табличное задание закона распределения дискретной случайной величины

X	х₁	х₂	…		х_n
P(X)	р₁	р₂	…		р_n

Пример: среди 20 животных 3 имеют рост 120 см, 4 - рост- 130 см, 10 - рост 140 см, и 3 - рост 150 см.

Таблица, характеризующая закон распределения будет выглядеть так:

X	120	130	140	150
P(X)	3/20	4/20	10/20	3/20

2. В виде графика:

Рис. 5.1. Графическое представление закона распределения дискретной случайной величины.

Для непрерывных случайных величин невозможно создать подобную таблицу, так как она может принимать бесконечное множество дробных значений из некоторого интервала, и, вероятность каждого из них близка к нулю.

Поэтому, закон распределения вероятностей такой величины должен позволить найти вероятность попадания ее значения в любой заданный интервал (х1, х2), лежащий внутри (а, b):

Рис. 5.2.

Эту вероятность обозначают Р (х ₁ < Х < х ₂). Ее можно вычислить через величину, которая называется плотностью распределения вероятностей случайной величины Х, и обозначается как f (х)

Вероятность попадания значений величины Х в конечный интервал (х₁, х₂) (рис.7. 2) определяется следующей формулой:

(5.2)

Графически это можно интерпретировать как площадь под графиком функции f(x) на участке от х₁ до х_2. Изменяя пределы интегрирования, можно найти вероятность для любых интересующих нас интервалов. Поэтому именно задание функции f(х) полностью определяет закон распределения для непрерывных случайных величин.

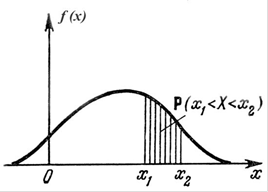
Рис. 5.3. Графическое представление закона распределения для непрерывной случайной величины.

Случайные числа могут быть распределены самым разным образом, но существует один закон распределения, который играет очень важную роль.

Пример. Опишем представителей, какой-либо популяции животных (всего 200 особей) по одному признаку. например, росту.

Результаты приведены на рис. 7.4 (мы округлили рост до целого числа сантиметров). Каждому животному соответствует кружок так, что, например, два кружка над числом 30 означают, что имеются два животных ростом 30 см. Рис 5.4 это распределение животных по росту. Мы видим, что рост большинства животных — от 35 до 45 см. Животных очень низкого роста (ниже 30 см) совсем немного— всего трое, и столько же животных очень высокого роста (выше 50 см).

Рис.5.4. Распределение животных по росту

Если измерить другие признаки, скорее всего, мы получим график, похожий по форме на этот. Такой закон распределения называется законом Гаусса. Это наиболее часто встречающийся на практике закон распределения случайных величин. Кроме того, он является предельным законом, то есть нему, при определенных условиях приближаются другие законы распределения.

Нормальный закон распределения характеризуется следующей формулой для плотности вероятности:

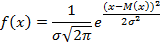
(5.3)

В этой формуле вы встретили неизвестные вам обозначения: M(x) - математическое ожидание случайной величины и - стандартное отклонение, суть которых будет объяснена в следующем разделе.

3. Основные числовые характеристики случайных величин

Раз существует множество похожих распределений, значит, для характеристики каждого из них достаточно указать чем оно отличается от других ему подобных, то есть всю собранную информацию мы можем свести к нескольким числам, которые называются параметрами распределения. Самыми главными из них являются математическое ожидание и стандартное отклонение.

Математическое ожидание М (Х) случайной величины Х является вероятностным аналогом ее среднего арифметического:

(5.4)

где n-количество значений случайной величины

Интерес представляет также то, насколько другие значения отличаются от среднего. Для оценки этого существует показатель, который называют дисперсией.

Дисперсия характеризует рассеяние, разбросанность значений случайной величины Х относительно ее математического ожидания:

(5.5)

Однако, дисперсия имеет размерность квадрата случайной величины, поэтому для анализа данных удобнее использовать величину стандартного отклонения.

Стандартное отклонение вычисляется как квадратный корень из дисперсии:

(7.5)

Если анализируется не вся совокупность данных, а выборка из нее рассчитывают выборочную дисперсию:

И стандартное отклонение по выборке: корень из выборочной дисперсии:

Часто полезно вычислить также стандартную ошибку выборки. Она определяется так: 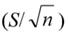: разделить стандартное отклонение на корень из объема выборки.

Кроме этих показателей распределение стандартной величины характеризуется также следующими.

Мода Мо (Х) дискретной случайной величины это ее наиболее вероятное значение (рис. 5.5, а), а непрерывной — значение Х, при котором плотность вероятности максимальна (рис. 5.5, б).

Медианой (Ме) случайной величины обычно пользуются только для непрерывных случайных величин. Медианой Ме(Х) случайной величины называют такое значение Х, которое делит все распределение на две равновероятные части, т. е. вероятности Р(Х ≤ Ме) и Р(Х ≥ Ме) оказываются равными между собой (рис. 5.5, в).

Рис. 5.5. а) мода дискретной случайной величины, б) мода непрерывной случайной велинины, в) медиана случайной величины

Асимметрия As (коэффициент асимметрии) характеризует «скошенность» распределения. Если распределение симметрично относительно математического ожидания, коэффициент асимметрии равен нулю (рис. 5.6).

Эксцесс Ex (коэффициент эксцесса) используется для характеристики так называемой «крутости», т. е. островершинности или плосковершинности распределения (рис 5.7).

Рис. 5.6. На первом графике коэффициент ассиметрии >0, на втором - <0

Рис. 5.7. На втором графике представлено нормальное распределение, на первом - распределение с коэффициентом эксцесса >0, а на третьем - с коэффициентом эксцесса<0

Рассмотрим некоторые закономерности этих числовых характеристик, которые свойственны нормальному закону распределения.

График функции 5.2 называется нормальной кривой распределения (кривой Гаусса).

Он имеет симметричный вид относительно прямой х = М (Х).(среднего значения величины)

При изменении значения М(Х) нормальная кривая не меняется по форме, но сдвигается вдоль оси абсцисс.

С возрастанием σ (σ₁) максимальное значение f(x) убывает, а сама кривая, становясь более пологой, растягивается вдоль оси абсцисс, при уменьшении σ (σ3) кривая вытягивается вверх, одновременно сжимаясь с боков (рис. 5.8).