Пример 1
Независимые случайные величины 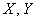 принимают только целые значения:
принимают только целые значения:
 – от 1 до 13 с равными вероятностями;
– от 1 до 13 с равными вероятностями;
 – от 1 до 16 с равными вероятностями.
– от 1 до 16 с равными вероятностями.
Найти  – вероятность того, что в очередном испытании сумма появившихся чисел будет меньше шести.
– вероятность того, что в очередном испытании сумма появившихся чисел будет меньше шести.
Решение:предложенные случайные величины можно ассоциировать с нестандартными игральными костями, на одной из которых 13, а на другой – 16 граней.
Из условия следует, что:
– вероятность того, что случайная величина  примет какое-либо значение равна
примет какое-либо значение равна  ;
;
– вероятность того, что случайная величина  примет какое-либо значение равна
примет какое-либо значение равна 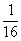 .
.
Так как случайные величины независимы, то по теореме умножения вероятностей независимых событий, вероятность появления любой пары чисел  в очередном испытании постоянна и равна:
в очередном испытании постоянна и равна: 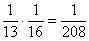 . Заметьте, что рассмотрение пар уже констатирует тот факт, что мы рассматриваем СИСТЕМУ случайных величин, а не их по отдельности.
. Заметьте, что рассмотрение пар уже констатирует тот факт, что мы рассматриваем СИСТЕМУ случайных величин, а не их по отдельности.
Подсчитаем количество пар, соответствующих событию  :
:
сумме  соответствует единственная пара
соответствует единственная пара 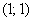 ;
;
сумме  – пары
– пары  ;
;
сумме  – пары
– пары 
и сумме  :
:  .
.
Итого: 10 нужных пар.
По теореме сложения вероятностей несовместных событий:
 – вероятность того, что сумма появившихся чисел будет меньше шести
– вероятность того, что сумма появившихся чисел будет меньше шести
Ответ: 
Но то, конечно, была разминка:
Пример 2
Две независимые дискретные случайные величины  и
и  заданы своими законами распределения вероятностей:
заданы своими законами распределения вероятностей:

Нет, это не опечатка, случайные величины имеют одинаковые законы распределения. Здесь их удобно ассоциировать с двумя одинаковыми и независимо работающими игровыми автоматами, на которых с определенными вероятностями загораются пронумерованные лампочки.
Требуется:
1) Найти закон распределения вероятностей системы случайных величин и вычислить:
 – математическое ожидание случайной величины
– математическое ожидание случайной величины  , при условии, что другая величина приняла значение
, при условии, что другая величина приняла значение  ;
;
 – математическое ожидание случайной величины
– математическое ожидание случайной величины  , при условии
, при условии  .
.
2) Вычислить  – вероятности того, что случайная величина
– вероятности того, что случайная величина  примет значение из соответствующих двумерных областей.
примет значение из соответствующих двумерных областей.
3) Найти закон распределения вероятностей случайной величины 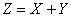 . Вычислить математическое ожидание
. Вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
4) Вычислить 
В реальной работе вам может встретиться и то, и другое, и третье и чётвёртое, поэтому разбираемся во всём осознанно и очень внимательно.
Решение:
1) Составим закон распределения вероятностей системы  случайных величин.
случайных величин.
«Иксовые» вероятности будем обозначать как обычно:
 ,
,
а к «игрековым» вероятностям добавим «птичку»:

Вычисления стандартно начнём с наименьшего «икса» и «игрека». Найдём  – вероятность того, что случайная величина
– вероятность того, что случайная величина  примет значение
примет значение  и случайная величина
и случайная величина  значение
значение  . По условию, случайные величины независимы, и коль скоро так, то по теореме умножения вероятностей независимых событий:
. По условию, случайные величины независимы, и коль скоро так, то по теореме умножения вероятностей независимых событий:

Найдём  – вероятность того, что
– вероятность того, что 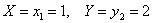 :
:

И так далее. Вычисления удобно проводить на калькуляторе или даже устно, а результаты заносить в таблицу. В качестве ещё одного примера я вычислил и отметил красным цветом вероятность  – того, что случайные величины примут значения
– того, что случайные величины примут значения  :
:

Это и есть закон распределения системы  . Не забываем проверить, что сумма всех вероятностей равна единице. Кстати, это ещё не значит, что ошибок нет. Для бОльшей уверенности следует просуммировать вероятности по строкам – в результате должны получиться
. Не забываем проверить, что сумма всех вероятностей равна единице. Кстати, это ещё не значит, что ошибок нет. Для бОльшей уверенности следует просуммировать вероятности по строкам – в результате должны получиться  , т.е. закон распределения случайной величины
, т.е. закон распределения случайной величины  ; и просуммировать вероятности по столбцам – в результате должны получиться «игрековые» вероятности
; и просуммировать вероятности по столбцам – в результате должны получиться «игрековые» вероятности  величины
величины  .
.
Для системы СВ не вводится понятия «общего» математического ожидания, однако можно подсчитать мат ожидания условные – при условии, что одна из величин примет или уже приняла некоторое конкретное значение.
Вычислим  – математическое ожидание случайной величины
– математическое ожидание случайной величины  , при условии, что другая величина приняла значение
, при условии, что другая величина приняла значение  . Так как случайные величины независимы, то распределение случайной величины
. Так как случайные величины независимы, то распределение случайной величины  не зависит от того, какое значение приняла случайная величина
не зависит от того, какое значение приняла случайная величина  . А значит, при любом возможном значении «игрек» условные математические ожидания:
. А значит, при любом возможном значении «игрек» условные математические ожидания:
 – в точности равны мат ожиданию самой случайной величины
– в точности равны мат ожиданию самой случайной величины  .
.
Логично? Представьте, что на 2-м игровом автомате зажглась лампочка (любая). Ну и что с того? Первый же автомат работает независимо!
Следует отметить, что с зависимыми величинами всё не так, и на следующем уроке мы разберём алгоритм вычисления условного мат ожидания, который формально пригоден и для независимых величин.
Ну а пока нам достаточно найти математическое ожидание 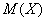 , и заодно сразу вычислим дисперсию, она потребуется позже:
, и заодно сразу вычислим дисперсию, она потребуется позже:

Таким образом:


С вероятностью  аналогично – представьте, что на «иксовом» игровом автомате зажглась лампочка №4. Ну и что? Это никак не повлияло на «игрековый» автомат и его матожидание, поэтому:
аналогично – представьте, что на «иксовом» игровом автомате зажглась лампочка №4. Ну и что? Это никак не повлияло на «игрековый» автомат и его матожидание, поэтому:
 – даже считать не пришлось, т.к. наши случайные величины имеют одинаковые распределения вероятностей.
– даже считать не пришлось, т.к. наши случайные величины имеют одинаковые распределения вероятностей.
2) Вычислим вероятность 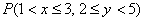 – того, что случайная величина
– того, что случайная величина  примет значение из области, которую задают неравенства в скобках.
примет значение из области, которую задают неравенства в скобках.
По аналогии с одномерным случаем, это можно сделать с помощью функции распределения вероятностей. Но для двумерной СВ составить такую функцию – не то, чтобы сложное, но весьма кропотливое занятие, и поэтому здесь проще просуммировать вероятности, соответствующие условиям  . На рисунке ниже я обвёл их красным цветом, и обратите внимание, что в силу строгости неравенства
. На рисунке ниже я обвёл их красным цветом, и обратите внимание, что в силу строгости неравенства  , строку
, строку  не следует включать в эту область. Таким образом:
не следует включать в эту область. Таким образом:  – вероятности я привык суммировать по строкам слева направо.
– вероятности я привык суммировать по строкам слева направо.

Аналогично, область  отграничена синим цветом, и здесь не следует учитывать значение
отграничена синим цветом, и здесь не следует учитывать значение 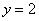 . В результате:
. В результате:  – вероятность того, что компонента
– вероятность того, что компонента  примет значения, не превосходящее двух, и компонента
примет значения, не превосходящее двух, и компонента  – значение, меньшее двух.
– значение, меньшее двух.
И с вероятностью  всё просто. Поскольку на переменную «икс» не наложено никаких ограничений, то она может быть любой, но вот то, что «игрек» окажется больше четырёх – есть событие невозможное. Поэтому
всё просто. Поскольку на переменную «икс» не наложено никаких ограничений, то она может быть любой, но вот то, что «игрек» окажется больше четырёх – есть событие невозможное. Поэтому  .
.
Точно по такому же принципу вычисляются вероятности и в случае зависимости случайных величин  ,
,  . Тут разницы нет.
. Тут разницы нет.
3) Найдем закон распределения вероятностей случайной величины 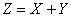 .
.
Принципиальным отличием от предыдущих пунктов является то, что здесь речь идёт об одномерной случайной величине. Как получаются её значения? С помощью суммирования случайных значений  , которые могут принять величины
, которые могут принять величины 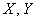 . И нам нужно перебрать все возможные варианты.
. И нам нужно перебрать все возможные варианты.
Начать удобно с самой маленькой возможной суммы, её образует пара  , в результате чего случайная величина «зет» примет значение
, в результате чего случайная величина «зет» примет значение  с вероятностью:
с вероятностью:

Может ли сумма равняться трём? Может. Исходу  соответствуют пары
соответствуют пары 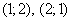 . По теоремам умножения вероятностей независимых и сложения несовместных событий:
. По теоремам умножения вероятностей независимых и сложения несовместных событий:

Сумме  соответствуют пары
соответствуют пары  и вероятность:
и вероятность:
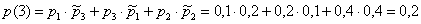
Сумма  тоже возможна, и ей соответствуют 4 пары:
тоже возможна, и ей соответствуют 4 пары:  . Наверное, вы заметили, что вероятности выпадения всех пар уже подсчитана в первом пункте, и, возможно, на практике вам будет удобнее предварительно составить таблицу распределения вероятностей системы
. Наверное, вы заметили, что вероятности выпадения всех пар уже подсчитана в первом пункте, и, возможно, на практике вам будет удобнее предварительно составить таблицу распределения вероятностей системы  . Но, разумеется, можно обойтись и без неё:
. Но, разумеется, можно обойтись и без неё:

Сумме  соответствуют пары
соответствуют пары  и вероятность:
и вероятность:

Сумме  – пары
– пары  :
:

и, наконец, сумме  – последняя возможная пара
– последняя возможная пара  :
:
 .
.
Искомый закон распределения 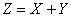 сведём в таблицу и сразу проведём стандартные вычисления для нахождения матожидания и дисперсии:
сведём в таблицу и сразу проведём стандартные вычисления для нахождения матожидания и дисперсии:

Обязательно контролируем, что  , ну и дальнейшее просто:
, ну и дальнейшее просто:


4) Вычислим 
Начнём с  . Как можно поступить? Можно составить закон распределения случайной величины
. Как можно поступить? Можно составить закон распределения случайной величины  . Паре
. Паре  соответствует значение
соответствует значение  , паре
, паре  – значение
– значение  , паре
, паре  – значение
– значение  и так далее…. И далее напрямую вычислить мат ожидание. Но есть путь короче.
и так далее…. И далее напрямую вычислить мат ожидание. Но есть путь короче.
Для математического ожидания справедливы следующие свойства:
 – математическое ожидание величины, которая принимает единственное значение
– математическое ожидание величины, которая принимает единственное значение  , равно этому значению. Логично
, равно этому значению. Логично
 – постоянный множитель можно вынести за знак матожидания.
– постоянный множитель можно вынести за знак матожидания.
 – это свойство справедливо как для независимых, так и для зависимых случайных величин. И сразу убедимся в справедливости этого факта. В первом пункте мы вычислили
– это свойство справедливо как для независимых, так и для зависимых случайных величин. И сразу убедимся в справедливости этого факта. В первом пункте мы вычислили  , во втором –
, во втором –  :
:
 , что и требовалось проверить.
, что и требовалось проверить.
Таким образом:

Но, следует отметить, что вам может быть предложено и «драконовское» задание, а именно, доказать, что  . При такой формулировке таки придётся составить закон распределения случайной величины
. При такой формулировке таки придётся составить закон распределения случайной величины  и вычислить
и вычислить  непосредственно.
непосредственно.
Едем дальше. С нахождением  никаких проблем: в первом пункте мы уже вычислили
никаких проблем: в первом пункте мы уже вычислили  и по свойствам матожидания:
и по свойствам матожидания:

Энтузиасты могут составить случайную величину  , и убедиться в справедливости равенства
, и убедиться в справедливости равенства  .
.
И осталось вычислить  .
.
Для дисперсии справедливы следующие свойства:
 – дисперсия постоянной величины равна нулю.
– дисперсия постоянной величины равна нулю.
 – константу можно вынести за знак дисперсии, возведя её в квадрат. Тоже логично: коль скоро, дисперсия – есть квадратичная величина, то при вынесении постоянного множителя, мы должны «расплатиться» возведением его в квадрат.
– константу можно вынести за знак дисперсии, возведя её в квадрат. Тоже логично: коль скоро, дисперсия – есть квадратичная величина, то при вынесении постоянного множителя, мы должны «расплатиться» возведением его в квадрат.
Для независимых случайных величин справедливо:
 , и сразу проверяем: в пункте 1 мы нашли
, и сразу проверяем: в пункте 1 мы нашли  , и в пункте 2 вычислили:
, и в пункте 2 вычислили:  .
.
Внимание! Для зависимых величин данное равенство неверно! Но об этом в другой раз.
И из последних двух свойств следует парадоксальное на первый взгляд равенство:
 , и тут прямо какой-то закон философии получился – когда из хаоса мы пытаемся вычесть другой хаос, то меры этих хаосов только суммируются.
, и тут прямо какой-то закон философии получился – когда из хаоса мы пытаемся вычесть другой хаос, то меры этих хаосов только суммируются.
И настал торжественный момент заключительных вычислений нашей большой задачи:

Готово.
Но готовы ли вы?:) Небольшая задачка для самостоятельного решения:
Пример 3
Две независимые дискретные случайные величины  и
и  заданы своими законами распределения вероятностей:
заданы своими законами распределения вероятностей:

Требуется:
1) Найти закон распределения вероятностей системы  и вычислить
и вычислить  .
.
Вычисления, кстати, удобно проводить в Экселе – «забиваем» числа и не «забиваем»:)
2) Найти закон распределения вероятностей случайной величины  , вычислить
, вычислить  и вероятность того, что полученная СВ примет отрицательное значение.
и вероятность того, что полученная СВ примет отрицательное значение.
3) Проверить справедливость равенства 
В последнем пункте сформулировано ещё одно свойство математического ожидания, которое справедливо только для независимых случайных величин.
Наверное, вы обратили внимание, что во всех задачах этой статьи в условии прямо констатируется независимость случайных величин. Но такого подарка может и не быть, и тогда нам предстоит выполнить самостоятельное исследование. Как его провести? Существуют строгие математические критерии, позволяющие выяснить, зависимы случайные величины или нет, и я приглашаю вас на следующий урок, где мы не только рассмотрим соответствующие примеры, но и узнаем много интересного.
Краткое решение Примера 3:
1) Используя теоремы умножения вероятностей независимых и сложения несовместных событий, составим закон распределения системы  :
:

Суммируя вероятности по строкам, убеждаемся, что получается закон распределения случайной величины  , и, суммируя вероятности по столбцам, получаем в точности закон распределения
, и, суммируя вероятности по столбцам, получаем в точности закон распределения 
Вычислим требуемые вероятности:

2) Найдём закон распределения случайной величины  .
.
Начнём с наименьшего значения  , которое даёт пара
, которое даёт пара  . Вероятности появления всех возможных комбинаций уже вычислены в предыдущем пункте:
. Вероятности появления всех возможных комбинаций уже вычислены в предыдущем пункте:
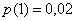
Произведению 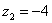 соответствуют пары
соответствуют пары  . По теореме сложения несовместных событий:
. По теореме сложения несовместных событий:

Произведению  соответствует пара
соответствует пара  :
:

Произведению  – пара
– пара  :
:

Произведению  соответствуют пары
соответствуют пары 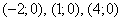 :
:

Произведению  – пара
– пара  :
:

Произведению  – пары
– пары  :
:
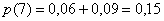
Произведению  – пара
– пара  :
:

Произведению 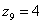 – пара
– пара  :
:

Произведению  – пара
– пара  :
:

и, наконец, произведению  – пара
– пара  :
:

Закон распределения случайной величины  сведём в 2 верхние строки расчётной таблицы, не забывая проконтролировать, что
сведём в 2 верхние строки расчётной таблицы, не забывая проконтролировать, что  :
:

Математическое ожидание:  , дисперсия:
, дисперсия:

 – вероятность того, что случайная величина
– вероятность того, что случайная величина  примет отрицательное значение.
примет отрицательное значение.
3) Покажем справедливость равенства  .
.
 – вычислено в предыдущем пункте.
– вычислено в предыдущем пункте.
Вычислим матожидания исходных случайных величин:

Таким образом:

 – получено верное равенство, что и требовалось проверить.
– получено верное равенство, что и требовалось проверить.
Домашнее задание.
1. Вычислить дисперсию Z из примера 3 по определению дисперсии. Сравнить полученный результат с примером 3.
2. Вычислить из данных примера 3 следующую величину Ϗ(Х,У)=М((Х-МХ)(У-МУ)). Попробуйте догадаться, что такое Ϗ(Х,У).
.
 2020-05-21
2020-05-21 147
147






