2020-05-25
92Урок №22 от 29.04.2020
· Изучите §11 п. 11.8 С. 322 - 326 «Введение вспомогательного угла».
· Выпишите в тетрадь основные формулы из §11 п. 11.8 С. 322 - 326 «Введение вспомогательного угла».
· Оформите в тетради (перепишите или распечатайте и вложите) решение следующих уравнений
Решите уравнения:
1) 
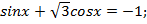
2) 
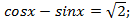
3) 
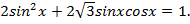
1) 
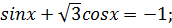
В данном уравнении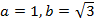 
, поэтому 
.
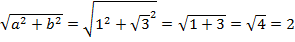Разделим каждый член данного уравнения на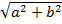 
, то есть на 2:
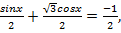перепишем в следующем виде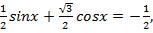 
Представим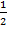 
в виде косинуса некоторого угла, а 
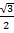- в виде синуса некоторого угла, тогда
, 
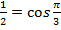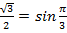и перепишем уравнение: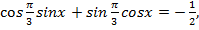 
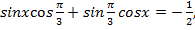
Воспользуемся формулой синус суммы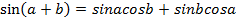 
и перепишем уравнение: 
;
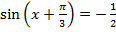Решим уравнение 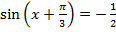, введём замену переменных 
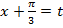и перепишем уравнение: 
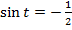, тогда 
, 
,
, 
,
, 
,
, 
,
, 
,
, 
,
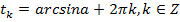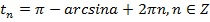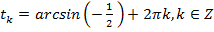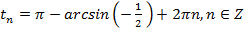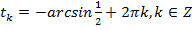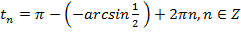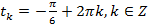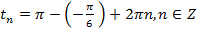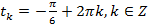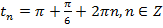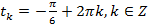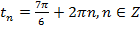Вернёмся к замене: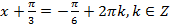 
и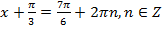 
,
Решим оба уравнения:
1) , 
, 
,
, 
,
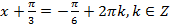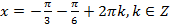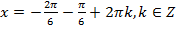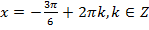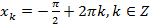2) , 
, 
,
.
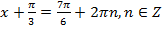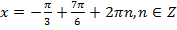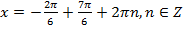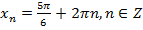Запишем ответ:
Ответ: , .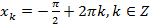
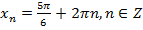2) 
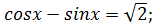
В данном уравнении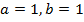 
, поэтому 
.
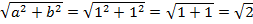Разделим каждый член данного уравнения на 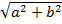, то есть на 
:
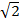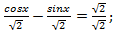перепишем в следующем виде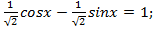 
Для удобства избавимся от иррациональности в знаменателе, а для этого домножим числители и знаменатели получившихся дробей на 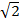и перепишем уравнение:
|
|
|
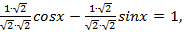
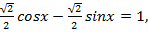
Представим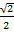 
в виде косинуса и синуса некоторого угла, тогда
, 
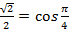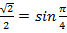и перепишем уравнение: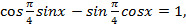 
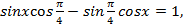
Воспользуемся формулой синус суммы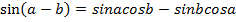 
и перепишем уравнение: 
;
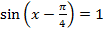Решим уравнение 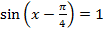, введём замену переменных 
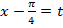и перепишем уравнение: 
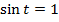, данное уравнение можно решить с помощью тригонометрического круга (синус соответствует оси 
, 
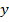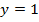в точке 
), 
,
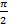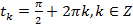Вернёмся к замене: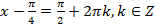 
, 
,
, 
.
.
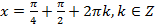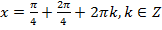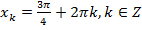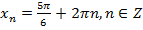Запишем ответ:
Ответ: .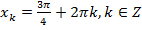
3) 
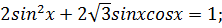
Воспользуемся формулой основное тригонометрическое тождество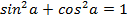 
и перепишем уравнение: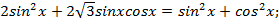 
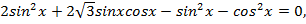
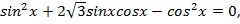
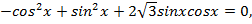
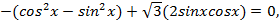
Воспользуемся формулами синус двойного угла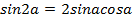 
и косинус двойного угла 
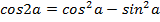и перепишем уравнение: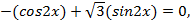 
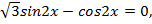
В данном уравнении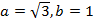 
, поэтому 
.
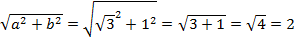Разделим каждый член данного уравнения на 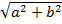, то есть на 2:
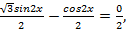
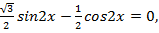
Представим 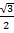в виде косинуса некоторого угла, а 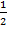- в виде синуса некоторого угла, тогда
, 
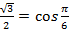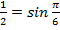и перепишем уравнение: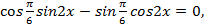 
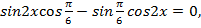
Воспользуемся формулой синус суммы 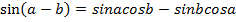и перепишем уравнение: 
;
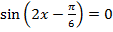Решим уравнение 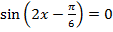, введём замену переменных 
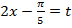и перепишем уравнение: 
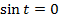, данное уравнение можно решить с помощью тригонометрического круга (синус соответствует оси , 
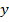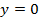в точке 
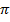и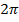 
), 
,
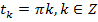Вернёмся к замене: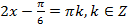 
, 
,
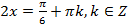Разделим уравнение на 2 и перепишем его: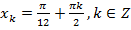 
.
Запишем ответ:
Ответ: .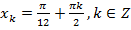
· Выполнить задание на карточке
Карточка
Решить уравнения:
1) 
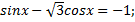
2) 
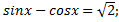
3) 
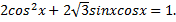
· Домашнее задания оформите в тетради.
· Сфотографируйте в разборчивом виде.
· Передайте мне до 29.04.2020 через эл.дненик, Whatsapp, или VK.
Критерии оценивания заданий карточки
Каждое уравнение может быть оценено в 1 балл, в случае верного решения и ответа.
|
|
|
Баллы суммируются. Максимальное количество баллов – 3.
Перевод баллов в оценки
3 балла – оценка «5»
2 балла – оценка «4»
1 балл – оценка «3»
менее 1 баллов – оценка «2»
