Логарифмические системы уравнений

Г.

 

Решение упражнений на тему: «Рациональные и иррациональные системы уравнений»

 

Рациональные системы уравнений

Задача 1. Решите системы:

а)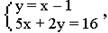

б)

Иррациональные системы уравнений

Задача 1. Решите систему иррациональных уравнений:

Решение: Чтобы избавиться от иррациональности введем новые переменные.

Пусть:

(1),

тогда первоначальная система примет вид:

.

Решая полученную систему, например методом подстановки находим: .

Подставим найденные значения в систему (1), получим:

.

Возведя обе части первого уравнения в квадрат, второго – в четвертую степень, получим систему:

,

откуда находим:

Нетрудно убедиться в том, что найденное решение последней системы является решением исходной системы.

Ответ: (6; 5)

Задача 2. Решите систему иррациональных уравнений:

Решение:

Из второго уравнения системы имеем: .  (1)

Подставим в первое уравнение системы вместо: правую часть равенства, получим:

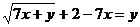или  (2).

Введем новую переменную:

положим:  (3)

и подставим в уравнение (2), получим квадратное уравнение от переменной : .

Находим корни этого уравнения, например, по теореме Виета: .

Корень:  - является посторонним, так как через обозначили арифметический корень.

Подставим, в (3), получим: .

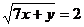Возведем обе части уравнения в квадрат и выразим : .

Подставим, полученное выражение во второе уравнение первоначальной системы:

.

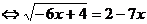Возведем обе части полученного уравнения в квадрат, при этом, чтобы не расширить область допустимых значений полученного уравнения, потребуем, чтобы:  (4).

; .

В силу (4) корень:  - является посторонним.

Найдем значение у при: : .

Нетрудно убедиться в том, что пара (0; 4) является решением первоначальной системы уравнений.

Ответ: (0; 4).

 

Решение упражнений на тему: «Показательные и логарифмические системы уравнений»

 

Показательные системы уравнений

Логарифмические системы уравнений

Задача 1. Решить систему логарифмических уравнений:

.

.

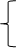
Решение:

1. Решим первое неравенство по определению логарифма:

Проверка:  - верно;

               - верно.

Решение первого уравнения имеет вид: х ₁ = -1; х ₂= 3.

2.Решим второе логарифмическое уравнение методом потенцирования:

ОДЗ (область допустимых значений переменной): .

Преобразуем исходное уравнение:

- удовлетворяет условию (1).

Решение второго уравнения имеет вид: .

3. Находим общее решение обоих уравнений: х = .

Ответ: х = .

Задача 2. Решите логарифмическое уравнение методом введения неизвестного (подстановкой):

.

Решение:

1.Решим первое логарифмическое уравнение методом введения неизвестного (подстановкой):

ОДЗ:  

В первом слагаемом перейдем к основанию 25, воспользовавшись формулой:  

Получим: .

Так как 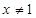, т.е.  то умножив обе части уравнения на  получим: .

Введем новую переменную, обозначив:  

Получим квадратное уравнение относительно нового неизвестного : .

Решая его, находим

Используя обозначение  получаем:

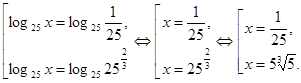
Найденные значения удовлетворяют ОДЗ.

Решение первого уравнения имеет вид: х _1,2 =

2.Решим второе логарифмическое уравнение методом приведения к одному основанию: ОДЗ: .

Перейдем к основанию 2, используя формулу: , получим:

,

,

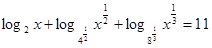обозначим: , тогда:

            .

Значит,

Найденное значение удовлетворяет ОДЗ.

Решение второго уравнения имеет вид: х = 64.

3. Находим общее решение обоих уравнений: х = .

Ответ: х = .

 

Более подробно можно посмотреть: Богомолов, Н.В.Математика: учебник для СПО / Н.В. Богомолов, П.И. Самойленко. — 5-е изд., перераб. и доп. — М.: Изд-во Юрайт, 2019. — 401 с. — (Серия: Профессиональное образование). — ISBN 978-5-534-07878-7. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://www.biblio-online.ru/bcode/433286.