Основные сведения из теории.
1. Определённый интеграл и его геометрический смысл.
Приращение F (b) – F (a) любой из первообразных функций
F(x)+ C при изменении аргумента от x = a до x = b называется определённым интегралом от a до b функции f (x) и обозначается:
 .
.
Числа a и b называются пределами интегрирования, а – нижним, b – верхним. Отрезок [a;b] называется отрезком интегрирования. Функция f (x) называется подынтегральной функцией, а переменная x – переменной интегрирования.
Таким образом, по определению
 .
.
Данное равенство называется формулой Ньютона - Лейбница.
Геометрический смысл определенного интеграла:
Если интегрируемая на отрезке [a;b] функция f (x) неотрицательна, то определённый интеграл: 
численно равен площади S криволинейной трапеции, ограниченной графиком функции f (x), осью абсцисс и прямыми x = a и x = b:


2. Свойства определённого интеграла.
1°. Постоянный множитель можно выносить за знак интеграла, т.е. если
A = const, то

2°. Определённый интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме их интегралов, т.е.

3°. Если a<c<b, то

4°. Если функция f (x) неотрицательная на отрезке [a;b], где a<b, то

5°. Если f (x)≥ g (x) для всех x € [a;b], где a<b, то

6°. Если m и M – наименьшее и наибольшее значения функции f (x) на отрезке [a;b], где a<b, то

7°. (Теорема о среднем). Если функция f (x) непрерывна на отрезке [a;b], то существует точка  такая, что
такая, что

Примеры вычисления определенных интегралов.
Пример 1: Вычислить 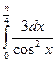 .
.

Пример 2: Вычислить 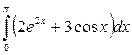

Пример 3: Вычислить  :
:

Пример 4: Вычислить:  :
:

 .
.

Задания для самостоятельного решения.
Вариант 1
1. Методом непосредственного интегрирования вычислить следующие интегралы:
а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д)  , е)
, е)  .
.
2. Методом подстановки вычислить:
а)  , б)
, б)  , в)
, в)  , г)
, г)  , д)
, д)  ,
,
е)  , ж)
, ж)  , з)
, з)  .
.
Вариант 2.
1. Методом непосредственного интегрирования вычислить следующие интегралы:
а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д)  , е)
, е)  .
.
2. Методом подстановки вычислить:
а)  , б)
, б)  , в)
, в)  , г)
, г)  ,
,
д)  , е)
, е)  , ж)
, ж)  , з)
, з)  .
.
Вариант 3.
1. Методом непосредственного интегрирования вычислить следующие интегралы:
а)  , б)
, б)  , в)
, в) 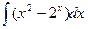 ,
,
г)  , д)
, д)  , е)
, е)  .
.
2. Методом подстановки вычислить:
а)  , б)
, б)  , в)
, в) 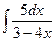 , г)
, г)  ,
,
д)  , е)
, е)  , ж)
, ж)  , з)
, з) 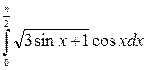 .
.
Вариант 4.
1. Методом непосредственного интегрирования вычислить следующие интегралы:
а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д)  , е)
, е)  .
.
2. Методом подстановки вычислить:
а)  , б)
, б)  , в)
, в)  , г)
, г)  ,
,
д) 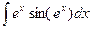 , е)
, е)  , ж)
, ж)  , з)
, з)  .
.
Контрольные вопросы.
1. Сформулируйте определение первообразной.
2. Дайте понятие неопределенного интеграла.
3. Какие основные формулы интегрирования вы знаете?
4. В чем заключается метод непосредственного интегрирования?
5. С каким способом интегрирования вы еще знакомы и в чем его суть?
6.В чем заключается геометрический смысл определенного интеграла?
7.Запишите формулу Ньютона-Лейбница
8.Какие основные свойства определенного интеграла вы знаете?
| № п/п | ФИО | Вариант |
| 1 | Аблаев Ислям | 1 |
| 2 | Аблялимов Имран | 2 |
| 3 | Аблялимов Ридван | 3 |
| 4 | Адамус Владислав | 4 |
| 5 | Антонова Диана | 1 |
| 6 | Борщева Кристина | 2 |
| 7 | Булава Александр | 3 |
| 8 | Давлетов Риза | 4 |
| 9 | Довгань Виталий | 1 |
| 10 | Кистечко Олег | 2 |
| 11 | Литовчук Виктория | 3 |
| 12 | Любарчук Владимир | 4 |
| 13 | Люманов Решат | 1 |
| 14 | Михайлин Михаил | 2 |
| 15 | Муртазин Кемал | 3 |
| 16 | Негрич Даниил | 4 |
| 17 | Орлов Кирилл | 1 |
| 18 | Савченко Егор | 2 |
| 19 | Сейтибраимов Нури | 3 |
| 20 | Селеметов Марлен | 4 |
| 21 | Федун Владлен | 1 |
| 22 | Филиппов Кирилл | - |
| 23 | Штефан Артем | 2 |
| 24 | Яценко Влада | 3 |
| 25 | Понедельников Максим | 4 |
 2020-05-21
2020-05-21 165
165







