Повторите тему «Перпендикулярность прямых и плоскостей», просмотрев презентацию. Разберите и запишите в тетрадь решение № 7, 8, 10, 12

Г. Геометрия. 10-А класс

Тема урока «Перпендикулярность прямых и плоскостей»

Запишите в тетрадь число, классная работа, тему урока.

Повторите тему «Перпендикулярность прямых и плоскостей», просмотрев презентацию. Разберите и запишите в тетрадь решение № 7, 8, 10, 12

№1

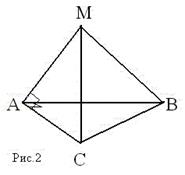
Дано: ∆ ABC - прямоугольный; AM ⊥ AC; M ∉ (ABC)
Доказать: AC ⊥ (AMB)
Доказательство: Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в плоскости (АМВ), то AC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости. Ч.т.д.

№2

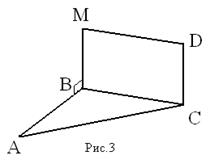
Дано: ВМDC - прямоугольник, M ∉ (ABC), MB ⊥ AB
доказать: CD ⊥ (ABC)
Доказательство: MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию, BC ⋂ AB, т.е. ВС и АВ лежат в плоскости (АВС) ⇒ MB ⊥ (ABC) по признаку перпендикулярности прямой и плоскости. СD ∥ МВ по свойству сторон прямоугольника ⇒ CD ⊥ (ABC) по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).
Ч.т.д.

№3

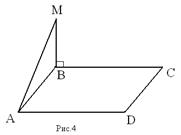
Дано: АВСD – прямоугольник, M ∉ (ABC), MB ⊥ BC
Доказать: AD ⊥ AM
Доказательство:
1) ∠ ABC = 90°, т.к. АВСD – прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB = B, т.е. МВ и АВ лежат в плоскости (АМВ) ⇒ BC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ (AMB) по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости).
3) Т.к. AD ⊥ (AMB) ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости.
Ч.т.д.

№4

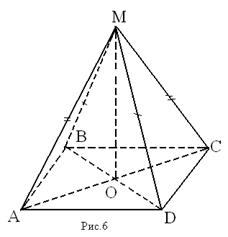
Дано: АВСD – параллелограмм, M ∉ (ABC), МВ = МD, МА = МС
Доказать: MO ⊥ (ABC)
Доказательство:
1) Т.к. О – точка пересечения диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD - равнобедренный, т. к. ВМ = МD по условию, значит МО - медиана и высота, т.е. MO ⊥ BD.
2) Аналогично доказывается в ∆ AMC: MO ⊥ AC.
3) Итак, MO ⊥ BD и MO ⊥ AC. а ВD и АС – пересекающиеся прямые, лежащие в плоскости (АВС) ⇒ MO ⊥ (ABC) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

№ 5.

Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P ₁ и Q ₁. Найдите P ₁ Q ₁, если PQ = 15cм; PP ₁ = 21,5 cм; QQ ₁ = 33,5 cм.

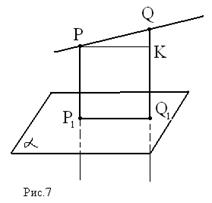
Решение:

1) PP ₁ ⊥ α и QQ ₁ ⊥ α по условию ⇒ PP ₁ ∥ QQ ₁;
2) PP ₁ и QQ ₁ определяют некоторую плоскость β, α ⋂ β = P ₁ Q ₁;
3) PP ₁ Q ₁ Q - трапеция с основаниями PP ₁ и QQ ₁, проведём PK ∥ P ₁ Q ₁;
4) QK = 33,5 - 21,5 = 12 (см)

P 1 Q 1 = PK =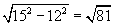

= 9 см.

Ответ: P ₁ Q ₁ = 9 см.

№ 6

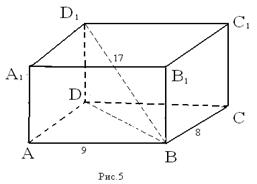
В прямоугольном параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ АВ = 9 см; ВС = 8 см; ВD = 17 см. Найдите площадь BDD ₁ B ₁.
Решение:

1) ∆ ABD: ∠ BAD = 90°; АD = BC = 8 см;

ВD =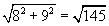

см;

2) ∆ DD ₁ B: ∠ D ₁DB = 90°;

DD 1 =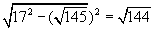

= 12 см;

 

3) SBB 1 D 1 D = BD ∙ DD 1 =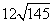

см2.

 

Ответ: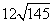

см2.

№ 7

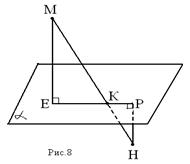
Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:

1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP, т.е. ∠ MEK = ∠ HPK = 90°;

3) ∆ HPK: KP =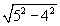

= 3 см;

4) ∠ EMK = ∠ PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),

тогда ∆ MEK ∆ HPK по двум углам и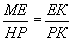

; т.е.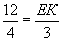

⇒ EK =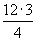

= 9 см,

РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.

Ответ: РЕ = 12 см.

№ 8

Через вершины А и В ромба АВСD проведены параллельные прямые AA ₁ и BB ₁, не лежащие в плоскости ромба. Известно, что BB ₁ ⊥ BC, BB ₁ ⊥ AB. Найдите A ₁ A, если A ₁ C = 13 см, BD = 16 см, AB = 10 см.

Решение:

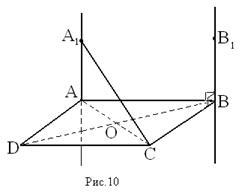
1) BB ₁ ⊥ AB, BB ₁ ⊥ BC, а AB ⋂ BC = B ⇒ BB ₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. BB ₁ ∥ AA ₁, то AA ₁ ⊥ (ABC) ⇒ AA ₁ ⊥ AC;
2) Используя свойство диагоналей ромба, имеем в ∆ AOB: ∠AOB = 90°, BO = ½ BD = 8 см. По теореме Пифагора:

AO =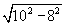

= 6 см,

AO = ½ AC ⇒ AC = 12 см;
3) ∆ A ₁ AC – прямоугольный. По теореме Пифагора:

AA 1 =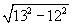

= 5 см.

Ответ: 5 см.

№ 9

 

Высота прямоугольного треугольника 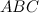, опущенная на гипотенузу, равна 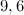. Из вершины 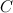прямого угла восставлен к плоскости треугольника 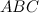перпендикуляр 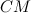, причем 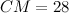. Найти расстояние от точки 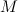до гипотенузы .

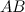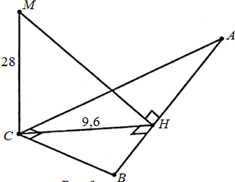
Решение. Пусть 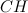- высота заданного прямоугольного треугольника .

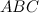Тогда 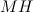- наклонная к плоскости треугольник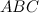а , а 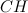- проекция этой наклонной на плоскость треугольника.

Так как , то по теореме о трех перпендикулярах и . Значит, длина отрезка 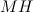равна искомому расстоянию от точки 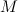до гипотенузы .

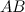Из прямоугольного треугольника 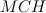по теореме Пифагора находим, что

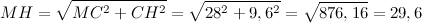
Ответ.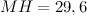

№ 10

Прямая АК перпендикулярна к плоскости правильного треугольника АВС, точка М – середина стороны ВС.

1) Докажите, что МК ⊥ ВС

2) Найдите угол между прямой КМ и плоскостью АВС, если АК = а, ВС = 2а.

1) Дано:

AB = BC = CA,

AK ⊥ ABC,

BM = MC.

Доказать: МК ⊥ ВС.

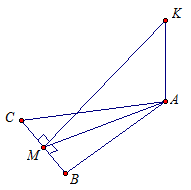
Доказательство:

АМ - это проекция наклонной КМ на плоскость АВС. АМ - медиана. По свойству правильного треугольника медиана АМ является и высотой, то есть прямые ВС и АМ перпендикулярны.

Прямая ВС перпендикулярна АМ - проекции наклонной МК. По теореме о трёх перпендикулярах получаем, что прямая ВС перпендикулярна и наклонной МК, что и требовалось доказать.

2) Дано:

АВ = ВС = СА,

АК ⊥ АВС,

ВС = 2а,

АК = а,

Найти: ∠(КМ; АВС)

Решение:

Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскости. Мы имеем наклонную МК, имеем ее проекцию АМ. Значит, углом между прямой МК и плоскостью АВС является угол АМК.

Треугольник АВС – правильный. Значит, все его углы равны 60°. Значит, ∠ АВС = 60°.

Рассмотрим треугольник АМВ. Он прямоугольный, так как АМ ⊥ ВС. Найдем АМ:

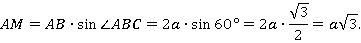
Рассмотрим прямоугольный треугольник АМК. AK = a,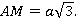

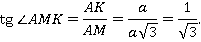
Угол АМК – острый, значит,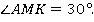

Ответ: 30°.

№ 11

Из точки М проведен перпендикуляр МВ к плоскости прямоугольника АВСD (рис. 4).

1) Докажите, что треугольники АМD и МСD – прямоугольные.

2) Найдите угол между прямой МD и плоскостью АВС, если СD = 3см,

АD = 4 см, МВ =5 см.

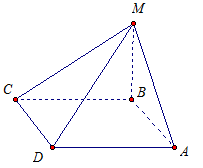
Рис. 4

1) Дано: прямоугольник АВСD, МВ ⊥ АВС.

Доказать: ∆АМD и ∆МСD – прямоугольные

Доказательство:

МВ – перпендикуляр к плоскости АВС. МА – наклонная, ВА - ее проекция. Проекция ВА перпендикулярна прямой АD из плоскости АВС. Значит, и наклонная МА перпендикулярна DА (по теореме о трех перпендикулярах). Таким образом, треугольник АМD - прямоугольный, так как угол МАD - прямой.

Аналогично, МС – наклонная, ВС - проекция наклонной МС на плоскость АВС. Проекция ВС перпендикулярна СD, значит, и наклонная МС перпендикулярна СD (по теореме о трех перпендикулярах). Угол МСD прямой, треугольник МСD прямоугольный.

2) Дано:

АВСD – прямоугольник, МD ⊥ АВС

СD = 3 см, АD = 4 см, МВ = 5 см.

Найти: ∠(DМ; АВС).

Решение:

Угол между прямой и плоскостью - это угол между прямой и ее проекцией на плоскость. DМ - наклонная, DВ ее проекция на плоскость АВС, следовательно, нам нужно найти угол МDВ. Обозначим его за φ.

Рассмотрим прямоугольный треугольник ВАD. АВ = СD = 3 см (как противоположные стороны прямоугольника). Найдем ВD по теореме Пифагора.

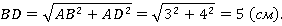
Рассмотрим прямоугольный треугольник МВD. Найдем угол ВDМ.

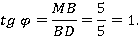
Угол φ – острый, значит,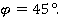

Ответ: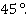

№ 12

Найдите двугранный угол АВСD тетраэдра АВСD, если углы DАВ, DАС и АСВ прямые, АС = СВ = 5 DВ = .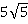

Дано: АВСD – тетраэдр.

∠ DАВ = ∠ DАС = ∠ АСВ = 90°.

АС = СВ = 5, DВ = .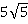

Найти: ∠ (АВСD)

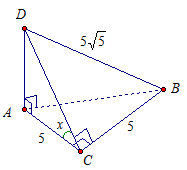
Решение:

Прямая DA перпендикулярна пересекающимся прямым АВ и АС из плоскости АВС. Значит, прямая DA перпендикулярна плоскости АВС.

Тогда АС - это проекция DС на плоскость АВС. Проекция АС перпендикулярна прямой ВС из плоскости по условию, значит, и наклонная DС перпендикулярна прямой ВС (по теореме о трех перпендикулярах). Получаем, что угол АСD – линейный угол искомого двугранного угла.

Рассмотрим прямоугольный треугольник DСВ. Найдем DС по теореме Пифагора.

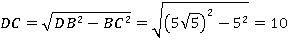
Рассмотрим прямоугольный треугольник АСD. Выразим косинус угла АСD.

.

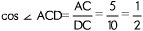Тогда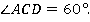

Ответ: .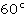

Повторить теорию из презентации. Решить задачи:

№ 1. Из точки А, взятой вне плоскости 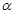, проведены к ней две наклонные, длины которых равны 10 и 17 см. Разность проекций этих наклонных на плоскость  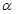равна 9 см. Найдите проекции наклонных.

№ 2. Расстояние от точки М до всех вершин квадрата равно 10 см. Найдите расстояние от точки М  до плоскости квадрата, если диагональ квадрата равна 12 см.

№ 3. Плоскость a проходит через основание АС равнобедренного треугольника АВС, ВО 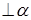, ВД- высота треугольника.

а) Докажите перпендикулярность прямой АС и плоскости ВДО.

б) Докажите перпендикулярность плоскостей ВСО и a.

в) Найдите периметр АВС, если ВО=3см, ДО= 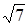см, СО=4см.

№ 4. Перпендикулярные плоскости a и b пересекаются по прямой l. Отрезки ОА и ОВ, лежащие в плоскостях a и b соответственно перпендикулярны прямой l, а их общий конец – точка О - лежит на прямой l. Найдите длину отрезка АВ, если ОА=20см, а ОВ:АВ=12:13.

 

Работы прислать на почту irinaboyarko@gmail.com