Тема: Формулы объема пирамиды и конуса.
Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава VII, § 3, п. 80-81), решить задачи самостоятельной работы и примерную задачу № 3, и ответить письменно на контрольные вопросы.
Теоретический минимум и задачи
Историческая справка.
Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287–212 гг. до н. э.) «О методе», в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470–380 гг. до н. э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулы для вычисления объема пирамиды и конуса.
Много сделала для геометрии школа Платона (428–348 гг. до н. э.). Платон был учеником Сократа (470–399 гг. до н. э.). Он в 387 г. до н. э. основал в Афинах Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: «Пусть сюда не входит никто, не знающий геометрии». Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260–170 гг. до н. э.) – учеником Евклида (III в. до н. э.), который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
Объем пирамиды
Объем пирамиды равен одной трети произведения площади ее основания на высоту.


Пусть площадь основания пирамиды равна  , а ее высота
, а ее высота 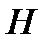 .
.
Поместим начало координат в вершину пирамиды, а ось  направим перпендикулярно плоскости основания пирамиды. Сечение пирамиды плоскостью, перпендикулярной ее высоте, на расстоянии
направим перпендикулярно плоскости основания пирамиды. Сечение пирамиды плоскостью, перпендикулярной ее высоте, на расстоянии  от вершины есть многоугольник, подобный основанию.
от вершины есть многоугольник, подобный основанию.
Следовательно,  ,
,
откуда 
 .
.
 Объем конуса
Объем конуса
Прямой круговой конус получается от вращения прямоугольного треугольника  вокруг оси
вокруг оси  . Составим уравнение прямой
. Составим уравнение прямой 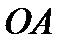 , образующей при своем вращении коническую поверхность. Обозначим
, образующей при своем вращении коническую поверхность. Обозначим 
 и напишем искомое уравнение прямой
и напишем искомое уравнение прямой 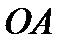 :
:  .
.
Применяя формулу  будем иметь:
будем иметь: 
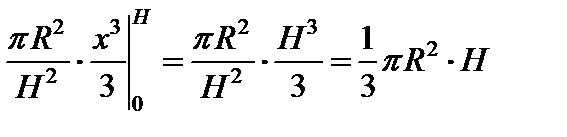 , т.е.
, т.е.

 2020-06-08
2020-06-08 144
144







