При выполнении заданий 21–26 используйте бланк ответов № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво

Вариант 22.Пробный ОГЭпо МАТЕМАТИКЕ

Инструкция по  выполнению данной работы 6 мая 2020.

Для прохождения аттестационного порога необходимо набрать не менее 8 баллов, из которых не менее 2 баллов должны быть получены за решение заданий по геометрии (задания 16 - 20, 24 - 26).

Оценка «4» - от 15 до21 балла.

Оценка «5» - от 22 баллов.

Экзаменационная работа состоит из двух частей, включающих в себя 26 заданий. Часть 1 содержит 20 заданий; часть 2 содержит 6 заданий с развернутым ответом.

Ответы к заданиям 7 и 15 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа.

Для остальных заданий части 1 ответом является число или последовательность цифр. Краткое решение запишите. А затем перенесите в бланк ответов № 1. Если получилась обыкновенная дробь, ответ запишите в виде десятичной.

Решения заданий части 2. Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер. После решения - «Ответ».

Все записи выполняются яркими черными чернилами. Допускается использование гелевой или капилярной ручки.

Сначала выполняйте задания части 1. Начать советуем с тех заданий, которые вызывают у Вас меньше затруднений, затем переходите к другим заданиям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.

Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.

При выполнении работы Вы можете воспользоваться справочными материалами.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Удачи!

Часть 1

Ответами к заданиям 1–20 являются цифра, число или последовательность цифр, которые следует записать в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.

 

 

Прочитайте внимательно текст и выполните задания 1-5.

 

На плане изображено домохозяйство по адресу: с. Федосеево, 6-й Зелёный пер., д. 2 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок справа от ворот находится хлев, а слева — сарай, отмеченный на плане цифрой 6. Площадь, занятая сараем, равна 36 кв. м.

Жилой дом находится в глубине территории. Помимо сарая, жилого дома и хлева, на участке имеется баня, расположенная в углу участка, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Также в углу огорода расположена компостная яма.

Все дорожки внутри участка вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и сараем и сараем и хлевом имеются площадки, вымощенные такой же плиткой.

К домохозяйству подведено электричество. Имеется магистральное газоснабжение.

 

1

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

 

Объекты	Хлев	Компостная яма	Баня	Жилой дом
Цифры

 

Ответ: ___________________________.

 

 

2

Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки, а также площадки перед баней и сараем и сараем и хлевом?

Ответ: ___________________________.

 

3

Найдите площадь, не занятую постройками и плиткой (в м²).

Ответ: ___________________________.

 

4

Хозяин участка планирует вырыть перед домом пруд диаметром 6 м. Найдите площадь, которую будет занимать этот пруд. Ответ дайте в виде  

Ответ: ___________________________.

 

5

Хозяин участка планирует провести в жилом доме отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.

 

	Нагреватель (котел)	Прочее оборудование и монтаж	Сред. расход газа / сред. потребл. мощность	Стоимость газа / электро-энергии
Газовое отопление	36 тыс. руб.	15 160 руб.	1,4 куб. м/ч	6,2 руб./куб. м
Электр. отопление	28 тыс. руб.	12 000 руб.	6,2 кВт	4,4 руб./(кВт · ч)

 

Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости оборудования и установки газового и электрического отопления?

 

Ответ: ___________________________.

 

 

Найдите значение выражения .

 

Ответ: ___________________________.

 

6

 

7

 

 

На координатной прямой отмечены точки , , , и .

Одна из них соответствует числу . Какая это точка?

 

1)

точка

2)

точка

3)

точка

4)

точка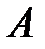

Ответ: ___________________________.

 

8

 

 

Найдите значение выражения .

 

Ответ: ___________________________.

 

 

9

 

 

Решите уравнение .

Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

 

 

Ответ: ___________________________.

 

 

10

 

 

Регистрационный номер автомобиля с кодом региона 34 содержит три одинаковые буквы «М» и три цифры. Какова вероятность того, что эти три цифры идут подряд в порядке убывания?

 

Ответ: ___________________________.

11

 

 

Установите соответствие между функциями и их графиками.

 

ФУНКЦИИ

 

А)

Б)

В)

 

ГРАФИКИ

 

1)

2)

3)

 

В таблице под каждой буквой укажите соответствующий номер.

 

Ответ:	А	Б	В

 

12

 

 

Дана арифметическая прогрессия , разность которой равна 1,1 и . Найдите сумму первых восьми её членов.

 

Ответ: ___________________________.

 

13

 

Найдите значение выражения  при , .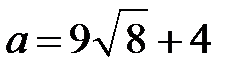

 

Ответ: ___________________________.

 

14

 

Мощность постоянного тока (в ваттах) вычисляется по формуле , где 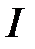  – сила тока (в амперах),   – сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление , если мощность составляет 650,25 Вт, а сила тока равна 8,5 А. Ответ дайте в омах.

 

Ответ: ___________________________.

 

15

 

 

Укажите решение системы неравенств       

 

 

1)		3)
2)		4)	нет решений

 

Ответ: ___________________________.

                                                            

 

 

 

16

 

 

В четырехугольник ABCD вписана окружность, AB = 22, CD = 17. Найдите периметр четырехугольника ABCD.

 

 

Ответ: ___________________________.

 

 

17

 

 

Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.

 

 

Ответ: ___________________________.

 

18

 

 

Периметр квадрата равен 84. Найдите площадь этого квадрата.     Ответ: ___________________________.

 

19

 

 

На клетчатой бумаге с размером клетки  изображён пятиугольник ABCDF. Найдите синус угла AFD.   Ответ: ___________________________.

 

20

 

 

Какие из следующих утверждений верны?

 

 

1)	В любой прямоугольной трапеции есть два равных угла.
2)	Касательная к окружности параллельна радиусу, проведённому в точку касания.
3)	Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

 

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Ответ: ___________________________.

 

 

Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы. Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.

 

 

 

Часть 2

При выполнении заданий 21–26 используйте БЛАНК ОТВЕТОВ № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.

 

21

 

 

Решите систему уравнений

 

 

22

 

Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?

.

 

 

23

 

 

Постройте график функции .

Определите, при каких значениях  прямая  имеет с графиком ровно три общие точки.

 

24

Около окружности диаметром 15 описана равнобедренная трапеция с боковой стороной, равной 17. Найдите длину меньшего основания трапеции.

 

25

 

Точки М и К середины сторон АВ и ВС треугольника АВС соответственно. Докажите, что отрезок МК делит отрезок ВТ, где Т – произвольная точка отрезка АС, пополам.

 

26

 

Найдите площадь четырехугольника, если известно, что отрезки, соединяющие середины его смежных сторон, равны 2 и 3, а угол между ними 30⁰.