2020-06-08
495
| № пп | Результаты измерений l, м | 
см
|
v 2, 
|
| 1 | 126,40 | – 9 | 81 |
| 2 | 126,43 | – 12 | 144 |
| 3 | 126,38 | – 7 | 49 |
| 4 | 126,30 | + 1 | 1 |
| 5 | 126,36 | – 5 | 25 |
| 6 | 126,31 | 0 | 0 |
| 7 | 126,28 | + 3 | 9 |
| 8 | 126,24 | + 7 | 49 |
| 9 | 126,20 | + 11 | 121 |
| 10 | 126,23 | + 8 | 64 |
| 11 | 126,26 | + 5 | 25 |
| 12 | 126,33 | – 2 | 4 |
L = 126,31 [ v ] = 0 [ v 2] = 572
см; 
см;
.
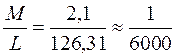Ответ: L = 126,31 м; 
см; 
см; 
.
8.2. Оценка точности функций измеренных величин
Среднюю квадратическую погрешность 
функции u независимых аргументов x, y, z, … вычисляют по формуле:
,
где 
– значения частных производных функции по переменным; 
– средние квадратические погрешности аргументов.
Порядок вычислений:
1. Установить аналитическое выражение функции, т. е. написать формулу, по которой вычисляется оцениваемая величина (функция) через аргументы, средние квадратические ошибки которых даны в условии задачи.
2. Записать формулу средней квадратической погрешности функции применительно к условиям данной задачи.
3. Взять частные производные функции по каждому аргументу (при этом остальные аргументы считаются постоянными).
4. Проанализировать надобность использования величины 
для представления угловых величин в радианной мере (напомним, что 
).
5. Подставить необходимые данные в формулу средней квадратической погрешности функции с соблюдением размерностей.
6. Записать ответ с указанием размерности.
Задача 1. Определить среднюю квадратическую погрешность превышения, вычисленного по горизонтальному расстоянию d = 124,16 м и углу наклона n = 2°16′, если md = 0,01 м, а m n = 10".
Решение. Превышение вычисляется по формуле тригонометрического нивелирования
h = d tgν.
Формула средней квадратической погрешности функции будет
.
Частные производные:
, 
.
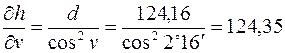Подставляя исходные данные, найдем
= 0,006 м.
В последней формуле учтено число секунд в радиане, равное 206265".
Ответ: 
м.
Задача 2. В треугольнике измерены два угла aи b с погрешностями 
и 
. Найти среднюю квадратическую погрешность третьего угла g, вычисленного как дополнение до 180° двух измеренных.
Решение. Функция имеет вид 
.
Формула средней квадратической погрешности функции
.
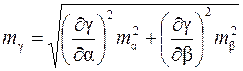Частные производные 
.
Тогда 
Ответ: 
.
Задача 3. Определить среднюю квадратическую погрешность превышения на станции технического геометрического нивелирования, если погрешность одного отсчета по рейке 1 мм.
Решение. Превышение h при геометрическом нивелировании находится как среднее значение превышений по черным и красным сторонам реек, а именно 
. В свою очередь превышения 
и 
вычисляются как разности отсчетов по задней (а) и передней (b) рейкам:
, 
.
Формула средней квадратической погрешности превышения 
запишется
.
Частные производные
, 
.
Тогда 
мм.
Аналогично можно вычислить среднюю квадратическую погрешность 
, которая также будет равна 
мм.
Запишем формулу средней квадратической погрешности 
превышения на станции
.
Частные производные 
; 
.
Тогда, окончательно 
мм.
Ответ: 
мм.
Задача 4. Вычислить среднюю квадратическую погрешность измерения расстояния нитяным дальномером, если средняя квадратическая погрешность в определении отрезка n по рейке, равного разности отсчетов по верхней и нижней нитям сетки, 
мм.
Решение. Расстояние, измеренное нитяным дальномером, определяется по формуле d = Kn, где K = 100 – коэффициент нитяного дальномера.
Средняя квадратическая ошибка функции d одного переменного n запишется
.
Т.к. 
, то md = Kmn.
Подставляя K = 100 и mn = 3 мм, получим:
м.
Ответ: 
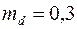м.
8.3. Обработка результатов неравноточных измерений одной величины
Неравноточными называются измерения, выполненные приборами разной точности, разным числом приемов, в различных условиях. Для обработки неравноточных измерений каждому измерению присваивают свой вес, вычисляемый по формуле 
, где с – произвольное число, назначаемое так, чтобы веса были близки к 1.
Математическая обработка ряда результатов l 1, l 2, …, l n прямых неравноточных измерений одной величины выполняется в следующей последовательности.
1. Вычисление весового среднего (общей арифметической средины)
.
2. Вычисление поправок к результатам измерений
ν i = L 0 – l i, (i = 1, 2,…, n).
Контролем правильности вычислений служит равенство
[ pv ]» 0.
3. Вычисление средней квадратической погрешности одного измерения по уклонениям от арифметической средины, используя формулу Бесселя для неравноточных измерений
4. Вычисление средней квадратической погрешности весового среднего
Обработку выполняют в таблицах установленной формы. Пример обработки многократных измерений угла, выполненных разным числом приемов и с различной точностью приведен в табл. 8.2.
В примере веса измерений вычислены по формуле 
, где С = 100.
Таблица 8.2
