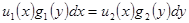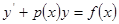2020-06-08
78Дифференциальные уравнения с разделяющимися переменными.
Пусть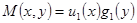 
, а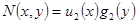 
, тогда уравнение (2) называется дифференциальным уравнением с разделяющимися переменными и примет вид:
|
Путем деления на произведение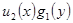 
оно приводится к следующему виду:
.
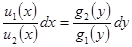Общий интеграл этого уравнения имеет вид:
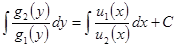
Внимание: Задания, помеченные звездочкой (*), обязательны для выполнения!
1. Решить дифференциальные уравнения с разделяющимися переменными:
Цель: Научиться находить общее решение дифференциального уравнения с разделяющимися переменными, используя в своей работе методы дифференциального и интегрального исчисления.
1) 
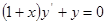
Решение: приведем уравнение к виду (1) (учитывая, что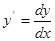 
):
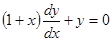
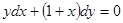
В данном уравнении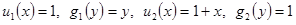 
Разделяя переменные, получим:
.
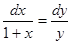Интегрируя, найдем общий интеграл:
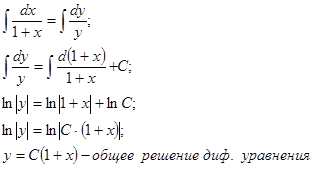
2) * 
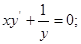
3) * 
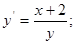
4) * 
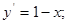
5) 
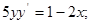
6) 
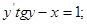
7) 
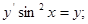
8) 
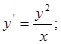
2. Найти частное решение дифференциального уравнения, удовлетворяющего начальным условиям, и его интегральную кривую.
Цель: Научиться находить частное решение дифференциального уравнения с разделяющимися переменными, используя в своей работе методы дифференциального и интегрального исчисления и строить интегральную кривую этого решения.
.
1) 
; 
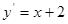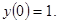
Решение: Приведем уравнение к виду (1) и разделим переменные:
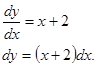
Интегрируя, найдем общий интеграл:
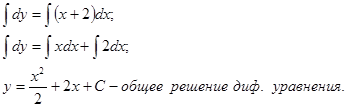
Т.к.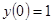 
, то подставляя это начальное условие в общее решение диф. уравнения, найдем значение С:
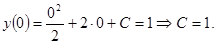
Значит частное решение данного диф. уравнения имеет вид:
.
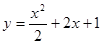Чтобы найти интегральную кривую данного диф. уравнения нужно построить график его частного решения, в нашем случае это 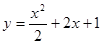(график – парабола).
Найдем координаты вершины параболы:
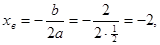
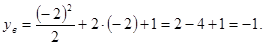
График имеет следующий вид:
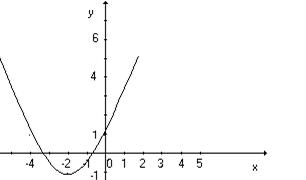
2) * 
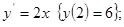
3) * 
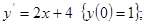
4) 
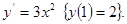
Линейные дифференциальные уравнения 1-го порядка.
Линейным дифференциальным уравнением 1-го порядка называется уравнение
|
, где p(x), f(x) – известные функции.
Линейное дифференциальное уравнение называется однородным, если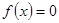 
, в противном случае оно неоднородное.
3. Найти общее решение линейного дифференциального уравнения 1-го порядка:
Цель: Научиться находить общее решение линейных дифференциальных уравнений, используя в своей работе методы дифференциального и интегрального исчисления.
1) 
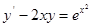
Решение: Общее решение неоднородного уравнения можно найти методом вариации постоянной.
· Рассмотрим однородное уравнение
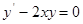, соответствующее данному неоднородному уравнению. Это уравнение с разделяющимися переменными:
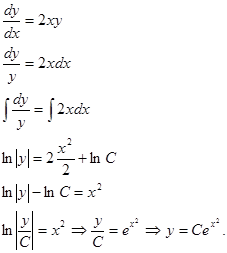
· Общее решение неоднородного уравнения ищем в виде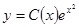 
(*), где С(х) – неизвестная функция от х. Производная 
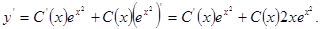Подставляя 
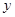и 
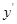в 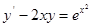найдем С(х):
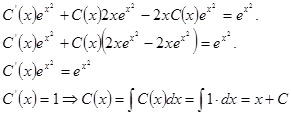
Т.к.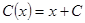 
, то подставляя его в (*) общее решение неоднородного уравнения будет 
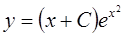, где С – постоянная интегрирования.
2) * 
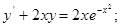
3) 
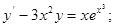
4) * 
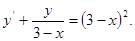
4. Определить вид дифференциального уравнения, найти его общее решение, а где указано частное решение.
Цель: Научиться определять вид дифференциального уравнения, находить его общее и частное решение.
1) * 
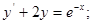
2) * 
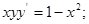
3) * 
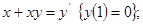
4) 
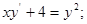
5) 
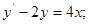
6) 
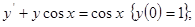
7) * 
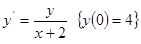, построить интегральную кривую;
8) * 
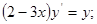
9) 
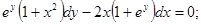
10) * 
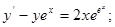
11) * 
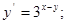
12) * 
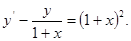
Задания для самостоятельного решения.
Найти общее решение дифференциальных уравнений, а где указано частное решение:
1. 
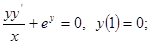
2. 
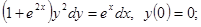
3. 
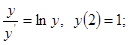
4. 
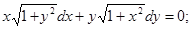
5. 
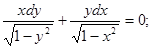
6. 
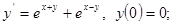
7. 
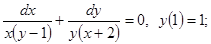
8. 
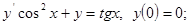
9. 
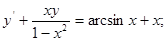
10. 
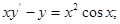
11. 
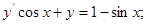
12. 
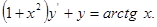
Контрольные вопросы:
1. Что называется дифференциальным уравнением первого порядка?
2. Что нужно сделать, чтобы решить дифференциальное уравнение.
3. Какой вид имеет дифференциальное уравнение с разделяющимися переменными.
4. Какое уравнение называется дифференциальным уравнением 1-го порядка?
5. Что такое общее и частное решение дифференциального уравнения.
