
в точках  (рис. 6).
(рис. 6).
 |
Решение. Применим теорему Дирихле к заданной на отрезке
 функции. Так как точки
функции. Так как точки  и
и  – концы отрезка, то ряд Фурье функции сходится к значению (рис. 7)
– концы отрезка, то ряд Фурье функции сходится к значению (рис. 7)

 |
Точка  – точка разрыва функции, значит, ее ряд Фурье сходится в этой точке к значению
– точка разрыва функции, значит, ее ряд Фурье сходится в этой точке к значению
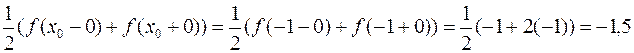 .
.
Точка  – также точка разрыва функции, значит, ряд Фурье сходится в этой точке к значению
– также точка разрыва функции, значит, ряд Фурье сходится в этой точке к значению
 .
.
Точка  – точка непрерывности функции, поэтому ее ряд Фурье сходится в этой точке к значению самой функции
– точка непрерывности функции, поэтому ее ряд Фурье сходится в этой точке к значению самой функции
 .
.
Точка  находится за пределами отрезка
находится за пределами отрезка  , и функция
, и функция  там не определена, но сумма
там не определена, но сумма  ряда Фурье функции
ряда Фурье функции  является периодической функцией с периодом
является периодической функцией с периодом  . Так как
. Так как  , ряд Фурье в точке
, ряд Фурье в точке  сходится к тому же значению, что и в точке
сходится к тому же значению, что и в точке  , а поскольку
, а поскольку  – точка непрерывности, это значение равно
– точка непрерывности, это значение равно 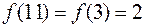 .
.
Сумма ряда Фурье, полученного в результате разложения функции, изображена на рис. 7.
Пример 2. Разложить в ряд Фурье функцию 
Решение. Разложение в ряд Фурье функции  , заданной на отрезке
, заданной на отрезке 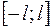 , имеет вид
, имеет вид
 ,
,
где


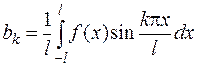
 .
.
Найдем коэффициенты разложения  . Так как на отрезке
. Так как на отрезке  функция
функция  задана разными аналитическими выражениями, разобьем область интегрирования в каждом случае точкой
задана разными аналитическими выражениями, разобьем область интегрирования в каждом случае точкой  на две подобласти и получим
на две подобласти и получим

=  ,
,

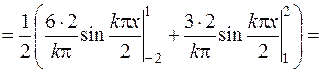
 ,
,





(при вычислении  заменили
заменили  более простой функцией
более простой функцией  ).
).
В результате получим разложение функции  в ряд Фурье
в ряд Фурье


 .
.
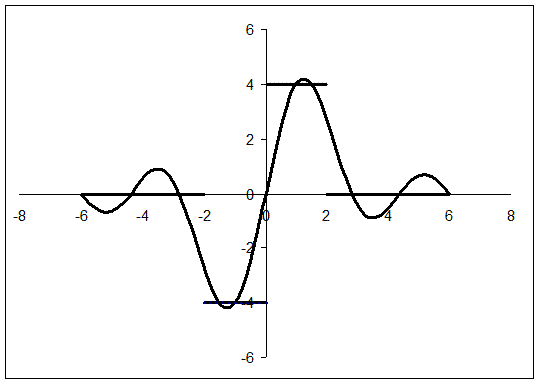
На рис. 8 изображена функция  и частичные суммы ряда Фурье для трех, четырех, шести и восьми ненулевых слагаемых соответственно.
и частичные суммы ряда Фурье для трех, четырех, шести и восьми ненулевых слагаемых соответственно.
Пример 3. Разложить в ряд Фурье по косинусам функцию

Решение. Разложим функцию, заданную на отрезке  , в ряд Фурье по косинусам (доопределяем
, в ряд Фурье по косинусам (доопределяем  на отрезок
на отрезок  как четную) с помощью формул:
как четную) с помощью формул:
 ,
,


 .
.
При этом


 .
.
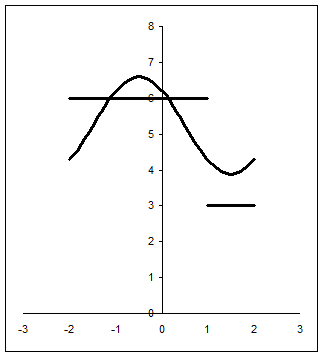 |  |
| а) График частичной суммы ряда Фурье из трех слагаемых | б) График частичной суммы ряда Фурье из четырех слагаемых |
 |  |
| в) График частичной суммы ряда Фурье из шести слагаемых | г) График частичной суммы ряда Фурье из восьми слагаемых |
Рис. 8. К примеру 2
Поэтому

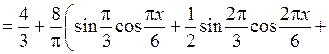

 .
.
На рис. 9 изображена функция  , продолженная четным образом на отрезок
, продолженная четным образом на отрезок  , и частичная сумма получившегося ряда Фурье (4 ненулевых слагаемых).
, и частичная сумма получившегося ряда Фурье (4 ненулевых слагаемых).
 |
| Рис. 9. К примеру 3 |
Пример 4. Разложить в ряд Фурье по синусам функцию

Решение. Разложим функцию, заданную на отрезке  в ряд Фурье по синусам (доопределяем
в ряд Фурье по синусам (доопределяем  на отрезок
на отрезок  , как нечетную) с помощью формул:
, как нечетную) с помощью формул:
 ,
,

 .
.
Тогда

 .
.
Таким образом,


 .
.
На рис. 10 изображена функция  , продолженная нечетным образом на отрезок
, продолженная нечетным образом на отрезок  , и частичная сумма получившегося ряда Фурье (3 ненулевых слагаемых).
, и частичная сумма получившегося ряда Фурье (3 ненулевых слагаемых).
 |
| Рис. 10. К примеру 4 |
Рекомендуемая к § 7 литература – см. библ. список [1, 3, 9, 14 – 15, 19, 22, 26, 28].
В задачах 533 – 544 с помощью теоремы Дирихле определить, к чему сходятся ряды Фурье указанных функций в точке  .
.
| 533. |   . . | Ответ. | 1 |
| 534. |   . . | Ответ. | –1 |
| 535. |   . . | Ответ. | 2 |
| 536. |  , ,  . . | Ответ. | 4,5 |
| 537. |   . . | Ответ. | 1 |
| 538. |  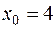 . . | Ответ. | 3 |
| 539. |   . . | Ответ. | 0 |
| 540. |   . . | Ответ. | –1 |
| 541. | 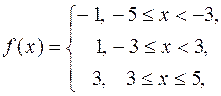 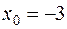 . . | Ответ. | 0 |
| 542. | 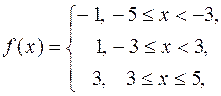  . . | Ответ. | 2 |
| 543. |   . . | Ответ. | 1 |
| 544. |  , ,  . . | Ответ. | 3 |
| 545. | Функция  разложена на отрезке разложена на отрезке  в тригонометрический ряд Фурье. Найти сумму ряда в точке в тригонометрический ряд Фурье. Найти сумму ряда в точке 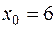 . Ответ. 0 . Ответ. 0 |
| 546. | Функция 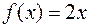 разложена на отрезке разложена на отрезке  в тригонометрический ряд Фурье. Найти сумму ряда в точке в тригонометрический ряд Фурье. Найти сумму ряда в точке  . Ответ. -2 . Ответ. -2 |
| 547. | Функция  разложена на отрезке разложена на отрезке  в тригонометрический ряд Фурье. Найти сумму ряда в точке в тригонометрический ряд Фурье. Найти сумму ряда в точке  . Ответ. -1 . Ответ. -1 |
| 548. | Функция  разложена на отрезке разложена на отрезке  в тригонометрический ряд Фурье. Найти сумму ряда в точке в тригонометрический ряд Фурье. Найти сумму ряда в точке 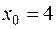 . Ответ. 0 . Ответ. 0 |
В задачах 549 – 568 найти коэффициенты  разложения в ряд Фурье функции
разложения в ряд Фурье функции  , заданной на отрезке
, заданной на отрезке 
( ).
).
| 549. |  | Ответ. |  |
| 550. |  | Ответ. |  |
| 551. |  | Ответ. |  |
| 552. |  | Ответ. |  |
| 553. |  | Ответ. |  |
| 554. |  | Ответ. |  |
| 555. |  | Ответ. |  |
| 556. |  | Ответ. |  |
| 557. | 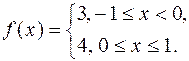 | Ответ. |  |
| 558. | 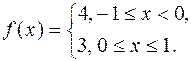 | Ответ. |  |
| 559. |  | Ответ. |  |
| 560. | 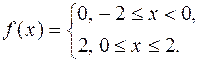 | Ответ. |  |
| 561. |  | Ответ. |  |
| 562. | 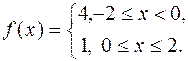 | Ответ. |  |
| 563. |  | Ответ. |  |
| 564. |  | Ответ. |  |
| 565. |  | Ответ. |  |
| 566. |  | Ответ. |  |
| 567. |  | Ответ. |  |
| 568. |  | Ответ. |  |
В задачах 569 – 576 разложить в ряд Фурье указанные функции.
| 569. |  | Ответ. | 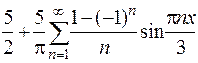 |
| 570. | 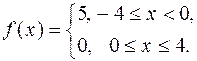 | Ответ. |  |
| 571. | 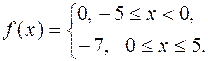 | Ответ. |  |
| 572. |  | Ответ. |  |
| 573. |  | Ответ. |  |
| 574. |  | Ответ. |  |
| 575. |  | Ответ. | 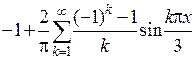 |
| 576. | 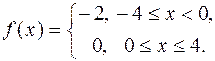 | Ответ. |  |
В задачах 577 – 588 найти коэффициенты 
 разложения в ряд Фурье по косинусам функции
разложения в ряд Фурье по косинусам функции  , заданной на отрезке
, заданной на отрезке 
( ).
).
| 577. |  | Ответ. |  |
| 578. |  | Ответ. |  |
| 579. |  | Ответ. |  |
| 580. |  | Ответ. |  |
| 581. |  | Ответ. | 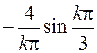 |
| 582. | 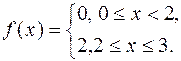 | Ответ. |  |
| 583. |  | Ответ. |  |
| 584. |  | Ответ. |  |
| 585. |  | Ответ. |  |
| 586. |  | Ответ. |  |
| 587. |  | Ответ. |  |
| 588. |  | Ответ. |  |
В задачах 589 – 592 разложить в ряд Фурье по косинусам указанные функции.
| 589. |  | Ответ. |  |
| 590. |  | Ответ. | 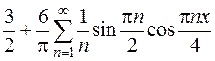 |
| 591. |  | Ответ. |  |
| 592. |  | Ответ. |  |
В задачах 593 – 605 найти коэффициенты  разложения в ряд Фурье по синусам функции
разложения в ряд Фурье по синусам функции  , заданной на отрезке
, заданной на отрезке 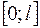
( ).
).
| 593. |  | Ответ. |  |
| 594. |  | Ответ. | 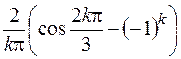 |
| 595. |  | Ответ. |  |
| 596. |  | Ответ. |  |
| 597. |  | Ответ. | 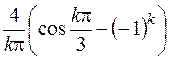 |
| 598. |  | Ответ. |  |
| 599. |  | Ответ. |  |
| 600. | 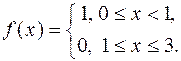 | Ответ. |  |
| 601. |  | Ответ. |  |
| 602. |  | Ответ. | 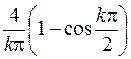 |
| 603. |  | Ответ. | 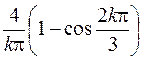 |
| 604. |  | Ответ. | 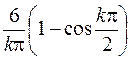 |
| 605. |  | Ответ. |  |
В задачах 606 – 609 разложить в ряд Фурье по синусам указанные функции.
| 606. |  | Ответ. |  |
| 607. |  | Ответ. |  |
| 608. |  | Ответ. |  |
| 609. |  | Ответ. |  |
Глава 3. Дифференциальные уравнения
Уравнение, содержащее переменные, их функцию, а также производные этой функции (или дифференциалы), называется дифференциальным уравнением. Если функция зависит от одной переменной, то уравнение называется обыкновенным дифференциальным уравнением. Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение.
§ 8. Дифференциальные уравнения первого порядка
Рассмотрим дифференциальное уравнение первого порядка
 ,
,
где функция у зависит от одной независимой переменной х.
Решить его (проинтегрировать) – значит найти функцию  , обращающую уравнение в тождество. Функция
, обращающую уравнение в тождество. Функция  , которая является решением уравнения при любом значении произвольной постоянной С, называется общим решением. Если в результате интегрирования получилось соотношение вида
, которая является решением уравнения при любом значении произвольной постоянной С, называется общим решением. Если в результате интегрирования получилось соотношение вида  (неявное задание функции у), говорят, что получен общий интеграл дифференциального уравнения. Задача нахождения частного решения при заданных условиях (
(неявное задание функции у), говорят, что получен общий интеграл дифференциального уравнения. Задача нахождения частного решения при заданных условиях ( ) называется задачей Коши.
) называется задачей Коши.
Рассмотрим некоторые дифференциальные уравнения первого порядка и способы их решения.
Дифференциальное уравнение с разделяющимися переменными – это уравнение вида
 .
.
Переменные разделяются, если уравнение разделить на  :
:
 .
.
Теперь при 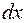 – только функции, зависящие от х, а при
– только функции, зависящие от х, а при  – от у. Значит, уравнение можно интегрировать:
– от у. Значит, уравнение можно интегрировать:
 .
.
Получен общий интеграл дифференциального уравнения (решение, записанное в неявном виде).
Линейное дифференциальное уравнение первого порядка есть уравнение вида
 .
.
Его можно решить методом Эйлера-Бернулли с помощью подстановки
 ,
,
где и и v – две неизвестные функции. При этом  . Подставляем полученные выражения в уравнение:
. Подставляем полученные выражения в уравнение:

и группируем слагаемые
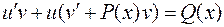 .
.
Так как одну из функций u или v можно выбрать произвольно (лишь произведение uv должно удовлетворять исходному уравнению), найдем v, приравняв к 0 выражение в скобках:
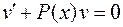 .
.
При этом предыдущее уравнение примет вид
 .
.
Решив первое из двух последних уравнений (оно с разделяющимися переменными), получим v, подставим v во второе уравнение (и оно с разделяющимися переменными) и найдем u. Осталось подставить найденные функции в формулу решения  .
.
Однородное дифференциальное уравнение первого порядка – это уравнение вида
 ,
,
где  – однородные функции одного порядка (
– однородные функции одного порядка ( ,
,  , k – порядок однородности).
, k – порядок однородности).
Такое уравнение приводится к виду

и решается с помощью замены  . При этом
. При этом  ,
, 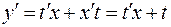 (x – переменная, поэтому
(x – переменная, поэтому  ).
).
В результате получаем уравнение
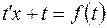 ,
,
где  . А это уравнение с разделяющимися переменными (способ решения описан выше).
. А это уравнение с разделяющимися переменными (способ решения описан выше).
Дифференциальное уравнение в полных дифференциалах – это уравнение вида
 ,
,
где  и
и  удовлетворяют условию
удовлетворяют условию
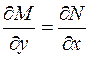 .
.
В этом случае левая часть уравнения является полным дифференциалом некоторой функции 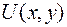 :
:
 ,
,
и уравнение можно переписать так:
 ,
,
а его решение (в результате интегрирования) примет вид:
 .
.
Функцию 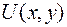 находят по формуле
находят по формуле

( выбирают таким образом, чтобы интегралы в правой части имели смысл). В итоге получаем решение дифференциального уравнения (общий интеграл):
выбирают таким образом, чтобы интегралы в правой части имели смысл). В итоге получаем решение дифференциального уравнения (общий интеграл):
 .
.
Пример 1. Дано дифференциальное уравнение  . Требуется: 1) найти общее решение дифференциального уравнения; 2) решить задачу Коши, если
. Требуется: 1) найти общее решение дифференциального уравнения; 2) решить задачу Коши, если  .
.
Решение. 1) Поскольку  , перейдем к уравнению
, перейдем к уравнению
 .
.
Это уравнение с разделяющимися переменными. Действительно, если разделить его на  и умножить на
и умножить на  , получим
, получим
 .
.
Переменные разделены (при 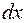 – только функции, зависящие от x, а при
– только функции, зависящие от x, а при  – от y), значит, уравнение можно интегрировать:
– от y), значит, уравнение можно интегрировать:
 .
.
В результате получим общий интеграл дифференциального уравнения (решение в неявном виде)
 .
.
Найдем общее решение, выразив y через x:
 .
.
2) Решаем задачу Коши – находим частное решение при условии, что  , то есть определяем C, подставляя в общее решение
, то есть определяем C, подставляя в общее решение  и
и  :
:
 .
.
При этом  , значит,
, значит,  и частное решение имеет вид
и частное решение имеет вид
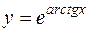 .
.
Пример 2. Найти общее решение дифференциального уравнения
 .
.
Решение. Это уравнение вида  – линейное дифференциальное уравнение I порядка. Будем решать его методом Эйлера-Бернулли с помощью подстановки
– линейное дифференциальное уравнение I порядка. Будем решать его методом Эйлера-Бернулли с помощью подстановки  , где u и v две неизвестные функции. При этом
, где u и v две неизвестные функции. При этом  . Подставляем полученные выражения в уравнение:
. Подставляем полученные выражения в уравнение:

и группируем слагаемые
 .
.
Так как одну из функций u или v можно выбрать произвольно (лишь произведение uv должно удовлетворять исходному уравнению), найдем v, приравняв к 0 выражение в скобках:
 .
.
При этом предыдущее уравнение примет вид
 .
.
Рассмотрим два последних уравнения.
Первое уравнение ( ) – дифференциальное уравнение с разделяющимися переменными. Действительно, так как
) – дифференциальное уравнение с разделяющимися переменными. Действительно, так как  , получим
, получим
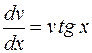 , или
, или  .
.
Переменные разделены, уравнение интегрируем:
 .
.
Находим какое-либо частное решение этого уравнения (полагая, например,  ). Получаем
). Получаем
 , или
, или  .
.
Тогда
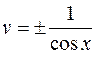 .
.
Подставим частное решение  во второе уравнение (
во второе уравнение ( ):
):
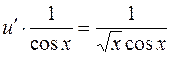 , откуда
, откуда  .
.
Полагая  , получим
, получим 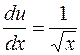 . Это дифференциальное уравнение с разделяющимися переменными. Разделяем переменные и интегрируем:
. Это дифференциальное уравнение с разделяющимися переменными. Разделяем переменные и интегрируем:
 ,
,  ,
,
откуда 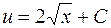 .
.
Осталось подставить найденные функции в формулу решения
 .
.
Пример 3. Найти общее решение дифференциального уравнения
 .
.
Решение. Это уравнение вида  , то есть однородное дифференциальное уравнение первого порядка. Решается с помощью замены
, то есть однородное дифференциальное уравнение первого порядка. Решается с помощью замены  . При этом
. При этом  ,
,  (x – переменная, поэтому
(x – переменная, поэтому  ). В результате получаем уравнение
). В результате получаем уравнение
 , или
, или  ,
,
где  , поэтому имеем
, поэтому имеем  . А это уравнение с разделяющимися переменными. Переменные разделяем
. А это уравнение с разделяющимися переменными. Переменные разделяем
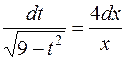 ,
,
уравнение интегрируем
 .
.
В результате приходим к соотношению
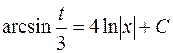 ,
,
откуда получаем общий интеграл дифференциального уравнения (решение в неявном виде)
 .
.
Выразив y через x, получим общее решение:
 ,
,  .
.
Пример 4. Найти общий интеграл дифференциального уравнения
 .
.
Решение. Если в уравнении
 ,
,
где 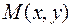 и
и  удовлетворяют условию
удовлетворяют условию
 ,
,
то это дифференциальное уравнение в полных дифференциалах.
В нашем случае
 и
и  ,
,
имеем
 .
.
Итак, задано дифференциальное уравнение в полных дифференциалах. Тогда его решение (общий интеграл) имеет вид
 .
.
Получаем
 ,
,
откуда
 ,
,
 ,
,
 ,
,
 .
.
Обозначив 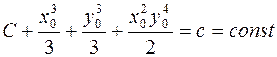 , окончательно получим
, окончательно получим
 –
–
общий интеграл дифференциального уравнения.
Рекомендуемая к § 8 литература – см. библ. список [1, 3, 7, 9, 11, 12, 15, 18, 19, 22].
В задачах 610 – 666 найти общие решения линейных дифференциальных уравнений первого порядка.
| 610. |  . . | Ответ. |  |
| 611. |  . . | Ответ. |  |
| 612. |  . . | Ответ. |  |
| 613. |  . . | Ответ. |  |
| 614. |  . . | Ответ. |  |
| 615. |  . . | Ответ. |  |
| 616. | 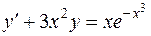 . . | Ответ. |  |
| 617. |  . . | Ответ. | 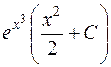 |
| 618. |  . . | Ответ. |  |
| 619. | 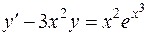 . . | Ответ. |  |
| 620. |  . . | Ответ. | 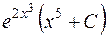 |
| 621. |  . . | Ответ. |  |
| 622. |  . . | Ответ. |  |
| 623. |  . . | Ответ. |  |
| 624. |  . . | Ответ. |  |
| 625. |  . . | Ответ. |  |
| 626. |  . . | Ответ. |  |
| 627. | 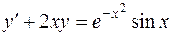 . . | Ответ. |  |
| 628. |  . . | Ответ. |  |
| 629. |  . . | Ответ. | 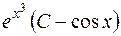 |
| 630. | 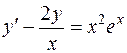 . . | Ответ. |  |
| 631. |  . . | Ответ. |  |
| 632. |  . . | Ответ. |  |
| 633. |  . . | Ответ. | 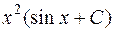 |
| 634. |  . . | Ответ. |  |
| 635. |  . . | Ответ. |  |
| 636. | 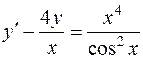 . . | Ответ. |  |
| 637. |  . . | Ответ. |  |
| 638. |  . . | Ответ. |  |
| 639. |  . . | Ответ. |  |
| 640. |  . . | Ответ. |  |
| 641. |  . . | Ответ. |  |
| 642. |  . . | Ответ. | 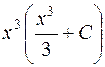 |
| 643. |  . . | Ответ. |  |
| 644. |  . . | Ответ. |  |
| 645. |  . . | Ответ. |  |
| 646. |  . . | Ответ. |  |
| 647. |  . . | Ответ. |  |
| 648. |  . . | Ответ. |  |
| 649. |  . . | Ответ. |  |
| 650. |  . . | Ответ. |  |
| 651. |  . . | Ответ. |  |
| 652. |  . . | Ответ. |  |
| 653. |
Подборка статей по вашей теме:
|
 2020-06-08
2020-06-08 1055
1055