Тема: Сечения призмы.
Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава I, § 4, п. 14), решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.
Теоретический минимум и задачи
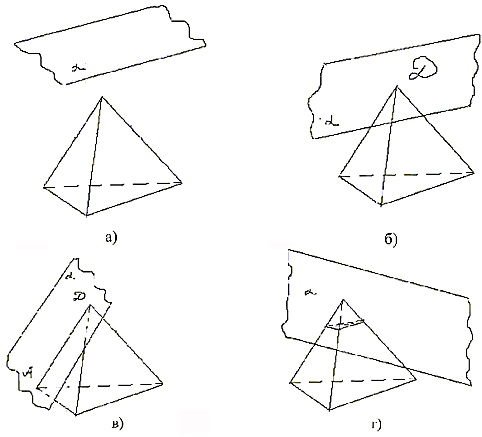
В пространстве две фигуры, для нашего случая плоскость и многогранник могут иметь следующее взаимное расположение: не пересекаются, пересекаются в точке, пересекаются по прямой и плоскость пересекает многогранник по его внутренности (рис.1), и при этом образуют следующие фигуры:
а) пустая фигура (не пересекаются)
б) точка
в) отрезок
г) многоугольник
Если в пересечении многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника с плоскостью.
Рис. 1
Определение. Сечением пространственного тела (например, многогранника) называется фигура, получающаяся в пересечении тела с плоскостью.
Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника.
Все способы построения сечений многогранников можно разделить на методы. Существует три основных метода построения сечений многогранников:
A) Метод следов.
B) Метод вспомогательных сечений.
Комбинированный метод.
Координатный метод.
Метод следов основывается (операеться) на аксиомах стереометрии, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют основным следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры. Последовательно соединяя образы этих точек, получим изображение искомого сечения.
Метод вспомогательных сечений построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.
Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.
Суть координатного метода заключается в вычислении координат точек пересечения ребер или многогранника с секущей плоскостью, которая задается уравнением плоскости. Уравнение плоскости сечения вычисляется на основе условий задачи.
Заметим, что это способ построения сечения многогранника приемлем для компьютера, так как он связан с большим объемом вычислений и поэтому этот метод целесообразно реализовать с помощью ЭВМ.
 Рассмотрим примеры построения сечений призмы разными методами.
Рассмотрим примеры построения сечений призмы разными методами.
Пример 1. Для параллелепипеда ABCDA1B1C1D1. Построить сечение проходящее через точки M, N, L.
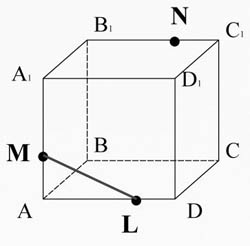
Решение:
Соединим точки M и L, лежащие в плоскости AA1D1D.
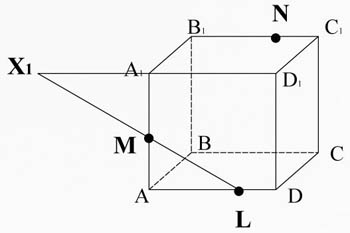
Пересечем прямую ML (принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
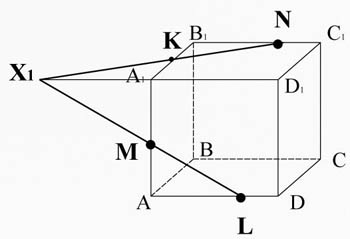
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
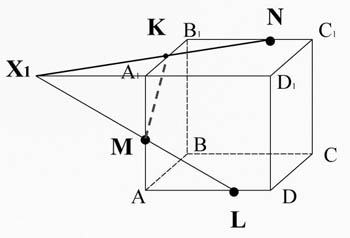
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
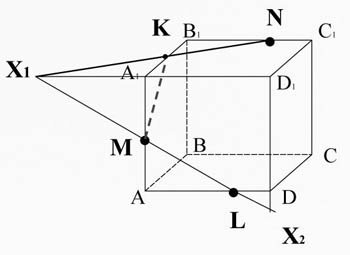
Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
Пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2.
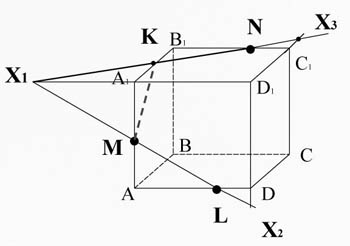
Пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;
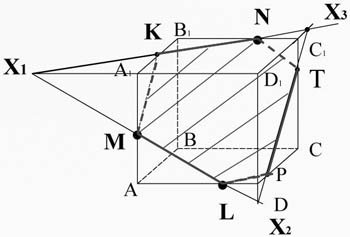 Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3, которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.
Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3, которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.
Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника, что и мы сделали. MKNTPL - искомое сечение.
Заметим. Эту же самую задачу на построение сечения, можно решить, воспользовавшись свойством параллельных плоскостей.
Из выше сказанного можно составить алгоритм (правило) решения задач, данного типа.
Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:
a) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
b) параллельные грани плоскость сечения пересекает по параллельным прямым.
Наибольшее число сторон многоугольника, полученного в сечении многогранника плоскостью, равно числу граней многогранника.
Пример 2. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки M, N, P (точки указаны на чертеже
Решение:
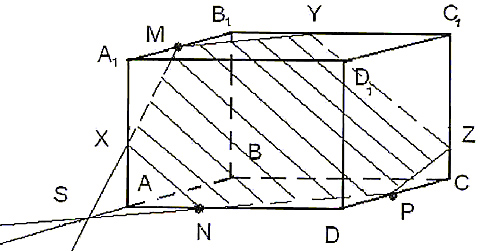
Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.
Проведём прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.
Так как точка M также принадлежит плоскости сечения и пересекает прямую АА1 в некоторой точке Х.
Точки X и N лежат в одной плоскости грани АА1D1D, соединим их и получим прямую XN.
Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A1B1C1D1, параллельную прямой NP. Эта прямая пересечет сторону В1С1 в точке Y.
Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.
Пример 3. Боковое ребро правильной призмы 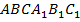 равно стороне основания. Построить сечение призмы плоскостью, проходящее через точку A, перпендикулярно прямой
равно стороне основания. Построить сечение призмы плоскостью, проходящее через точку A, перпендикулярно прямой 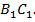 Найти площадь полученного сечения призмы, если
Найти площадь полученного сечения призмы, если 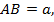
Решение.
Построим заданное сечение. Сделаем это из чисто геометрических соображений, например, следующим образом.
В плоскости 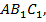 проходящей через заданную прямую
проходящей через заданную прямую 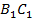 и заданную точку
и заданную точку 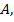 проведем через эту точку прямую, перпендикулярную прямой
проведем через эту точку прямую, перпендикулярную прямой 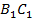 . Воспользуемся с этой целью тем, что в треугольнике
. Воспользуемся с этой целью тем, что в треугольнике 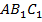
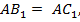 то есть его медиана
то есть его медиана 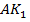 является и высотой этого треугольника. Таким образом, прямая
является и высотой этого треугольника. Таким образом, прямая 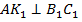 .
.
Через точку 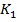 проведем еще одну прямую, перпендикулярную прямой
проведем еще одну прямую, перпендикулярную прямой 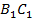 . Проведем ее, например, в плоскости
. Проведем ее, например, в плоскости 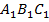 , проходящей через прямую
, проходящей через прямую 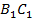 . Ясно, что этой прямой является прямая
. Ясно, что этой прямой является прямая 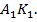
· Итак, построены две пересекающиеся прямые, перпендикулярные прямой 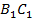 . Этими прямыми определяется плоскость
. Этими прямыми определяется плоскость 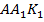 , проходящая через точку
, проходящая через точку 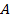 перпендикулярно прямой
перпендикулярно прямой 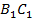 то есть задана секущая плоскость.
то есть задана секущая плоскость.
· Построим сечение призмы этой плоскостью. Заметим, что так как 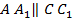 , то прямая
, то прямая 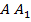 параллельна плоскости
параллельна плоскости 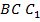 . Тогда плоскость
. Тогда плоскость 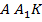 , проходящая через прямую
, проходящая через прямую 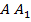 , пересекает плоскость
, пересекает плоскость 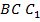 по прямой, параллельной прямой
по прямой, параллельной прямой 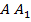 , то есть и прямой
, то есть и прямой 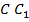 . Проведем через точку
. Проведем через точку 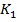 прямую
прямую 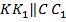 и полученную точку
и полученную точку 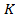 соединим с точкой
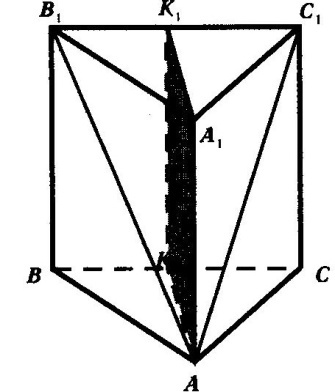
соединим с точкой 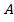 .
.
 Четырехугольник
Четырехугольник 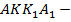 заданное сечение. Определим его площадь.
заданное сечение. Определим его площадь.
Понятно что четырехугольник 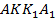 является прямоугольником, то есть его площадь
является прямоугольником, то есть его площадь 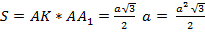
Построить сечение призмы, проходящее через три точки M; N; P:


Контрольные вопросы:
1. Что мы называем сечением многогранника?
2. Какие существуют методы построения сечений?
3. В чём состоит метод «след секущей плоскости»?
4. Где должны находиться точки секущей плоскости, чтобы их нужно было соединить для построения сечения?
5. Чему равно максимальное число сторон многоугольника, полученного в сечении многогранника?
 2020-06-08
2020-06-08 1609
1609






