Тема: «Интегральная формула объема. Вычисление объемов тел»

МАТЕМАТИКА

Группа 2-18

06.05.2020

Тема: «Вычисление площадей плоских фигур с помощью первообразной»

Написать конспект стр.210-213

Решить №№ 1036, 1037

Ссылка на учебник: https://yadi.sk/i/JdkuX-pqjn89FQ

Ссылка на задачник: https://yadi.sk/i/F6CEplrqyyUcbA

 

 

07.05.2020

Тема: «Нахождение площади плоских фигур»

Сделать конспект презентации.

Ссылка на презентацию: https://yadi.sk/i/jqq2XQmtS4bI-g

 

 

08.04.2020

Пара

Тема: «Интегральная формула объема. Вычисление объемов тел»

Сделать конспект:

Найти с помощью определённого интеграла объёмы пространственных тел.

Начнём с прямоугольного параллелепипеда, высота которого равна 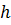, а площадь основания – .

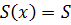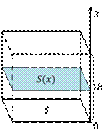
Площадь сечения прямоугольного параллелепипеда не изменяется в любой точке отрезка от 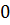до 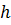и равна площади основания. Тогда получим, что объём прямоугольного параллелепипеда равен 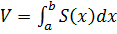. Вынесем 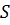за знак интеграла и получим, что объём прямоугольного параллелепипеда равен .

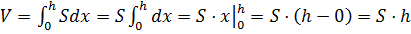Теперь попробуем с помощью интеграла вычислить объём прямой призмы.

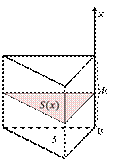
Пусть дана прямая 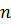-угольная призма с площадью основания 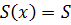и высотой .

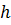Как и в случае прямоугольного параллелепипеда, площадь сечения прямой призмы не изменяется в любой точке отрезка от 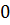до 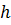и равна площади основания. Тогда получим, что объём прямой призмы равен 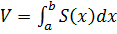. Вынесем 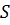за знак интеграла и получим, что объём прямой призмы равен .

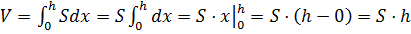Теперь рассмотрим цилиндр с высотой 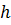и площадью основания .

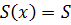Как и в случае прямоугольного параллелепипеда и прямой призмы, площадь сечения цилиндра не изменяется в любой точке отрезка от 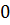до 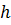и равна площади основания. Тогда получим, что объём цилиндра равен 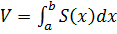. Вынесем 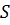за знак интеграла и получим, что объём цилиндра равен .

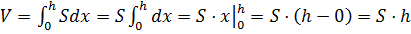Задача: сечение тела плоскостью, перпендикулярной к оси 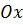и проходящей через точку с абсциссой 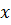, является квадратом, сторона которого равна . Найти объем этого тела.

Решение: воспользуемся только что доказанной формулой.

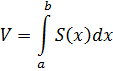
По рисунку видно, что пределами интегрирования будут числа 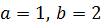. Поскольку сечение плоскости – квадрат, значит, площадь сечения равна .

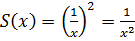Тогда получим, что объём этой фигуры равен .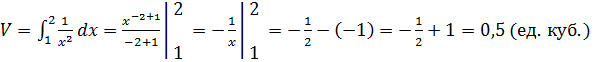

Задача: найти объём тела, полученного вращением данной кривой вокруг оси .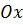

Решение: очевидно, что границами интегрирования будут числа .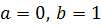

В сечении полученного тела плоскостью, перпендикулярной оси 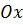будет круг, радиус которого равен ординате точки с абсциссой 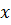, то есть радиусом этого круга будет .

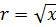Площадь такого круга равна 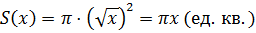. Поскольку 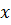принимает только неотрицательные значения, то можно записать, что площадь сечения равна .

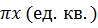Вычислим объём полученного тела как 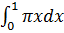. Применив формулу Ньютона-Лейбница, получим, что объём данного тела равен .

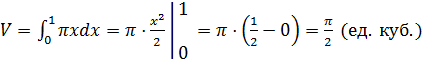Задача: найти объём тела, полученного вращением данной кривой вокруг оси .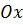

Решение: давайте внимательно посмотрим на получившееся тело.

Его можно получить из цилиндра, который получится при вращении прямоугольника вокруг своей стороны. Для этого надо из данного цилиндра «вынуть» фигуру, которую мы получили в предыдущей задаче.

Объём такой фигуры будет равен разности объёмов .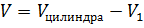

Радиусом основания цилиндра будет ордината точки с абсциссой равной 1. То есть радиус основания цилиндра равен 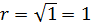. Высота цилиндра тоже равна 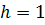. Тогда получим, что объём цилиндра равен .

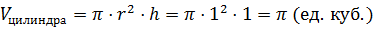Тогда объём искомой фигуры равен .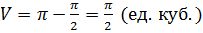

Пара