Диофантовы уравнения
(уравнения с двумя или большим числом неизвестных)
Дихтярь М.Б.
Первая часть.
Диофантовы уравнения – алгебраические уравнения с двумя или большим числом неизвестных с целыми коэффициентами, для которых находятся целые или рациональные решения.
Линейные диофантовы уравнения.
Линейным диофантовым уравнением с двумя неизвестными называется уравнение 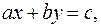 где
где 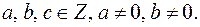
Уравнение 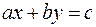 разрешимо (имеет решение) в целых числах тогда и только тогда, когда наибольший общий делитель чисел
разрешимо (имеет решение) в целых числах тогда и только тогда, когда наибольший общий делитель чисел 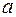 и
и 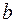
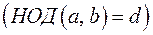 является делителем числа с.
является делителем числа с.
Отметим: если 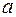 и
и 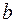 взаимно простые числа
взаимно простые числа 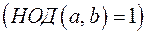 , то уравнение
, то уравнение 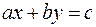 разрешимо в целых числах.
разрешимо в целых числах.
Упорядоченная пара чисел 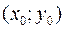 называется решением уравнения
называется решением уравнения 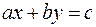 , если
, если 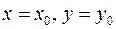 удовлетворяют уравнению (упорядоченная пара
удовлетворяют уравнению (упорядоченная пара 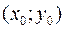 обращает уравнение в верное равенство).
обращает уравнение в верное равенство).
Решить уравнение в целых числах – это значит найти все целые решения или показать, что уравнение не имеет решений в целых числах.
Общим решением уравнения 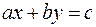 , где
, где 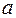 и
и 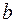 взаимно простые числа, х, у, с целые числа, является пара
взаимно простые числа, х, у, с целые числа, является пара 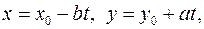 где
где 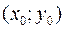 – любое частное решение, где
– любое частное решение, где 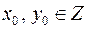 , t –любое целое число.
, t –любое целое число.
Задачи
1. Найдитеобщеерешение уравнения 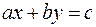 , где с целое число,
, где с целое число, 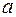 и
и 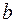 взаимно простые числа и
взаимно простые числа и 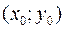 , где
, где 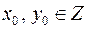 , частное решение этого уравнения.
, частное решение этого уравнения.
Решение. Так как 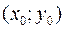 решение уравнения
решение уравнения 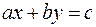 , то
, то 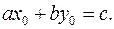 Из уравнения
Из уравнения 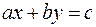 вычтем числовое равенство
вычтем числовое равенство 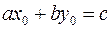 и получим:
и получим:
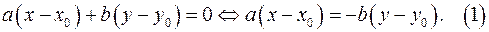
Так как 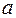 и
и 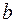 взаимно простые числа, то из уравнения (1) следует,
взаимно простые числа, то из уравнения (1) следует,
что 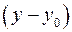 делится на а. Тогда существует целое число
делится на а. Тогда существует целое число 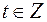 такое, что
такое, что 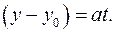 Из уравнения (1) находим:
Из уравнения (1) находим:
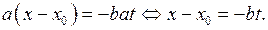
Таким образом, получили, что общим решением исходного уравнения является пара 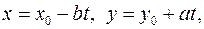 где
где 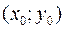 – любое частное решение, t – любое целое число.
– любое частное решение, t – любое целое число.
2. Найдите частное решение уравнения 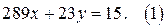
Решение. Уравнение (1) имеет решение в целых числах, так как коэффициенты при х и у взаимно простые числа.
1. Преобразуем исходное уравнение (выразим у через х)
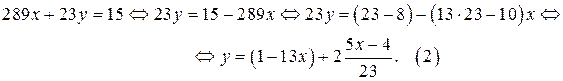
Уравнение (2), а значит и уравнения (1), имеет целые решения, если 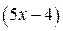 кратно 23.
кратно 23.
2. Найдём значение х, при котором 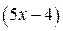 кратно 23:
кратно 23:
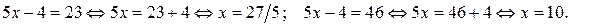
Итак, 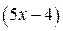 кратно 23,если
кратно 23,если 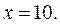
3. Если 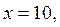 то из уравнения (2) или уравнения (1) находим у:
то из уравнения (2) или уравнения (1) находим у:
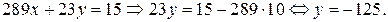
Итак, частным решением уравнения (1) является пара 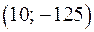 .
.
Ответ. 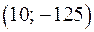 .
.
3. Решите в целых числах уравнение 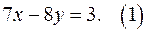
Решение. Уравнение (1) имеет решение в целых числах, так как коэффициенты при х и у взаимно простые числа.
1. Пусть 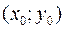 , где
, где 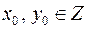 , частное решение уравнения (1).
, частное решение уравнения (1).
Так как 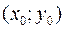 решение уравнения
решение уравнения 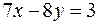 , то
, то 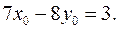
Из уравнения 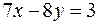 вычтем
вычтем 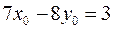 и получим:
и получим:
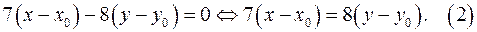
Так как 7 и 8 взаимно простые числа, то из уравнения (2) следует,
что 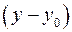 делится на 7. Тогда существует целое число
делится на 7. Тогда существует целое число 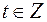 такое, что
такое, что 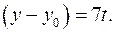 Из уравнения (2) находим:
Из уравнения (2) находим:
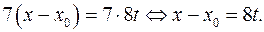
Итак, 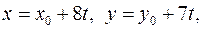 где
где 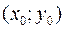 – любое частное решение, t – любое целое число.
– любое частное решение, t – любое целое число.
2. Найдём частное решение 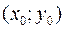 уравнения (1).
уравнения (1).
Преобразуем уравнение (1): 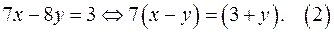
Так как левая часть уравнения (2) кратна 7, то уравнение имеет решение, если и правая уравнения (2) кратна 7. Правая часть уравнения (2) кратна 7, например, если 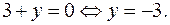 Если
Если 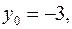 то из уравнения (2) находим, что
то из уравнения (2) находим, что 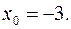 Итак, частным решением уравнения (1) является пара
Итак, частным решением уравнения (1) является пара 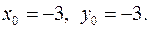
3. Так как 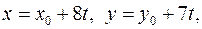 где
где 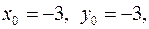 то общим решением уравнения (1) является пара
то общим решением уравнения (1) является пара 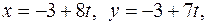 где
где 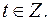
Ответ. 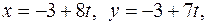 где
где 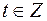 .
.
4. Решите в целых числах уравнение 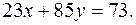
Решение. Уравнение имеет решение в целых числах, так как коэффициенты при х и у взаимно простые числа.
1. Преобразуем исходное уравнение (выразим х через у)
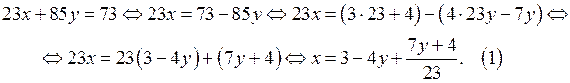
Число х является целым числом, если 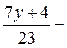 целое число. Число
целое число. Число 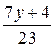 является целым, если
является целым, если 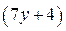 кратно 23.
кратно 23.
2. Преобразуем:
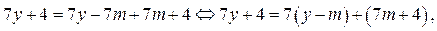 где
где 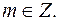
Найдём значение 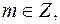 при котором
при котором 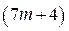 делятся на 23.
делятся на 23.
Число 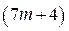 делится на 23, например, если
делится на 23, например, если 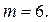 Тогда
Тогда
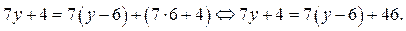
Так как 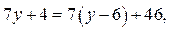 то из уравнения (1) имеем
то из уравнения (1) имеем
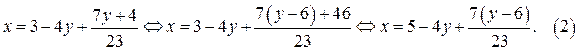
Число х является целым числом, если существует число 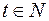 такое, что
такое, что 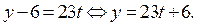
Если 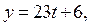 то из уравнения (2) находим:
то из уравнения (2) находим: 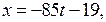 где
где 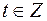 .
.
3. Таким образом, общим решением исходного уравнения является пара 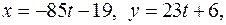 где
где 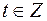 .
.
Ответ. 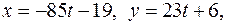 где
где 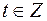 .
.
5. Докажите, что уравнение 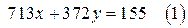 имеет решения в целых числах, а уравнение
имеет решения в целых числах, а уравнение 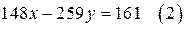 не имеет решений в целых числах. Найдите частное решение уравнения (1).
не имеет решений в целых числах. Найдите частное решение уравнения (1).
Решение. 1. Разложим на множители числа:
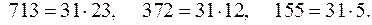
а) Так как числа 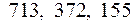 имеют общий множитель, равный 31, то обе части уравнения (1) разделим на 31 и получим уравнение
имеют общий множитель, равный 31, то обе части уравнения (1) разделим на 31 и получим уравнение 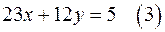 равносильное исходному уравнению. Уравнение (3), а значит и уравнение (1), имеет решение в целых числах, так коэффициенты в уравнении (3) при х и у взаимно простые числа.
равносильное исходному уравнению. Уравнение (3), а значит и уравнение (1), имеет решение в целых числах, так коэффициенты в уравнении (3) при х и у взаимно простые числа.
б) Найдём частное решение 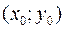 уравнения (1).
уравнения (1).
Преобразуем уравнение (1) (выразим у через х)
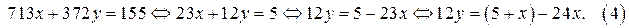 Уравнение (4), а значит и уравнение (1), имеет решение в целых числах, если
Уравнение (4), а значит и уравнение (1), имеет решение в целых числах, если 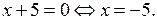 Если
Если 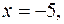 то из уравнения (4) находим: что
то из уравнения (4) находим: что 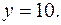 Итак, частным решением уравнения (1) является пара чисел
Итак, частным решением уравнения (1) является пара чисел 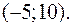
2. Разложим на множители числа:
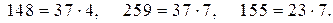
В уравнении (2) коэффициенты при х и у имеют общий множитель, равный 37, но свободный член не делится на 37. Тогда, если обе части уравнения (2) разделим на 37, то в полученном уравнении коэффициенты при х и у будут взаимно простыми числами, а свободный член не является целым числом. Поэтому уравнение (2) не имеет решений в целых числах.
Ответ. 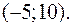
6. Найдите наименьшее положительное целое решение уравнения 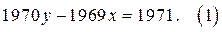
Решение. Разложим на множители: 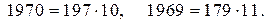
Уравнение (1) имеет решение в целых числах, так как коэффициенты при х и у взаимно простые числа.
Преобразуем уравнение (1) (выразим х через у)

Число х является целым, если 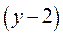 кратно 1969, то есть если существует число
кратно 1969, то есть если существует число 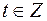 такое, что
такое, что 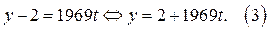
Из (3) следует: у принимает наименьшее положительное значение, равное 2, если 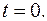
Если 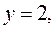 то из уравнения (2) находим, что
то из уравнения (2) находим, что 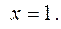
Пара 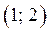 является наименьшим решением уравнения (2), а значит и уравнения (1), так как, если
является наименьшим решением уравнения (2), а значит и уравнения (1), так как, если 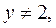 то из уравнения (2) следует, что
то из уравнения (2) следует, что 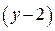 кратно 1969, если
кратно 1969, если 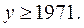
Ответ. 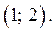
7. Найдите все целые решения уравнения 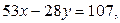 которые удовлетворяют условиям
которые удовлетворяют условиям 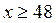 и
и 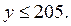
Решение. Уравнение имеет решение в целых числах, так как коэффициенты при х и у взаимно простые числа.
1. Найдём общее решение исходного уравнения.
а) Преобразуем уравнение (выразим у через х)
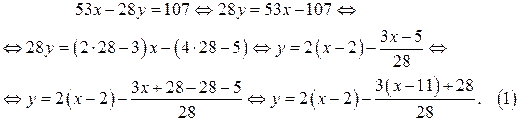
Так как 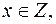 то у является целым числом, если существует число
то у является целым числом, если существует число 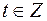 такое, что
такое, что 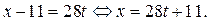
Если 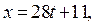 то из уравнения (1) находим:
то из уравнения (1) находим: 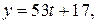 где
где 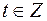 .
.
Таким образом, общим решением исходного уравнения является пара 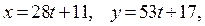 где
где 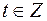 .
.
2. Так как 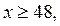
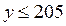 и
и 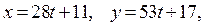 где
где 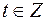 , то
, то
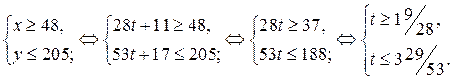
Так как 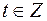 , то решениями последней системы являются
, то решениями последней системы являются 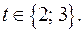
Так как 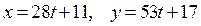 и
и 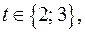 то искомыми решениями исходного уравнения являются пары
то искомыми решениями исходного уравнения являются пары 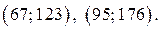
Ответ. 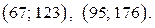
8. Найдите все целые решения уравнения 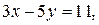 которые удовлетворяют условиям
которые удовлетворяют условиям 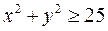 и
и 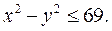
Решение. Уравнение имеет решение в целых числах, так как коэффициенты при х и у взаимно простые числа.
1. Найдём общее решение исходного уравнения.
Преобразуем уравнение (выразим х через у)
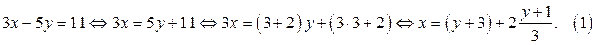
Так как 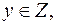 то х является целым числом, если существует число
то х является целым числом, если существует число 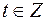 такое, что
такое, что 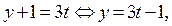 где
где 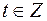 .
.
Если 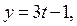 то из уравнения (1) находим:
то из уравнения (1) находим: 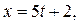 где
где 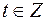 .
.
Таким образом, общим решением исходного уравнения является пара 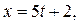
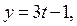 где
где 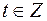 .
.
2. Так как 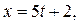
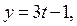 где
где 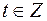 , то
, то
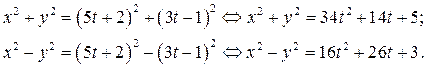
Так как 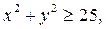
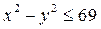 , то
, то
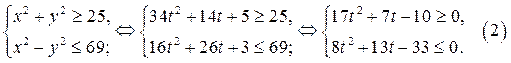
3. Найдём решения системы (2).
а) Найдём корни уравнения 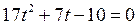 :
:
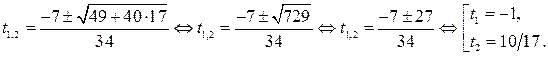
Так как 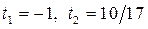 корни уравнения
корни уравнения 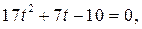 то решениями неравенства
то решениями неравенства 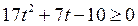 являются
являются 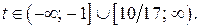
б) Найдём корни уравнения 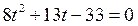 :
:
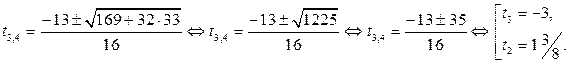
Так как 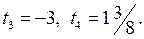 корни уравнения
корни уравнения 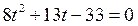 , то решениями неравенства
, то решениями неравенства 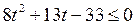 являются
являются 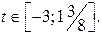
в) Решениями системы (2) являются
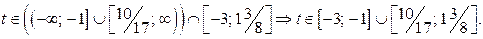
г) Так как 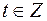 , из того, что
, из того, что 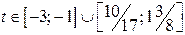 следует, что
следует, что 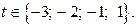
4. Найдём решения уравнения (1), если 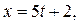
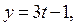 где
где 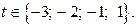
Если 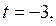 то
то 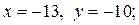 если
если 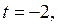 то
то 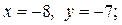
если 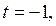 то
то 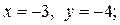 если
если 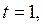 то
то 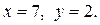
Итак, искомыми решениями уравнения 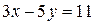 являются пары
являются пары 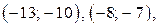
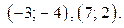
Ответ. 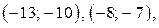
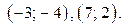
9. Найдите все пары натуральных чисел, удовлетворяющих уравнению 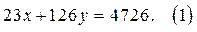
Решение. Уравнение (1) имеет решение в натуральных числах, так как коэффициенты при х и у взаимно простые числа.
1. Оценим натуральное число у. Так как 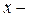 натуральное число, то
натуральное число, то 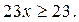 Тогда
Тогда
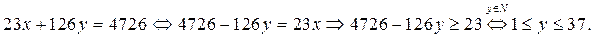
2. Преобразуем уравнение (1) (выразим х через у)
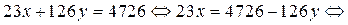
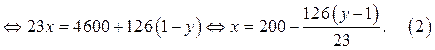
Так как 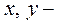 натуральные числа и 126 не кратно 23, то число
натуральные числа и 126 не кратно 23, то число 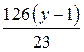 является целым, если
является целым, если 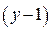 кратно 23. Так как
кратно 23. Так как 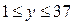 , то
, то 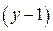 кратно 23, если
кратно 23, если 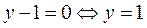 или
или 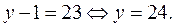
3. Из уравнения (2) следует: если 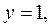 то
то 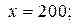 если
если 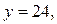 то
то
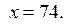
Ответ. 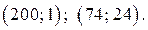
10. Найдите все целые решения уравнения 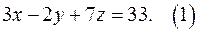
Решение. Найдём общее решение исходного уравнения.
Преобразуем уравнение (выразим х через у и z)
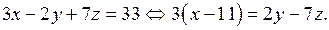
Пусть 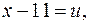 где
где 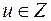 . Тогда уравнение (1) принимает вид
. Тогда уравнение (1) принимает вид
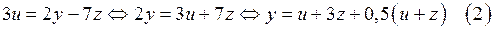
Так как 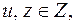 то у является целым числом, если существует число
то у является целым числом, если существует число 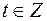 такое, что
такое, что 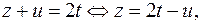 где
где 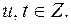 Тогда из уравнения (2) находим
Тогда из уравнения (2) находим 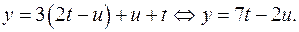
Таким образом, общим решением исходного уравнения является тройка чисел 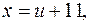 .
. 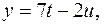
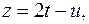 где
где 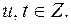
Ответ. 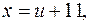
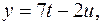
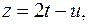 где
где 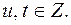
11. Найдите всевозможные числа 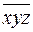 , которые удовлетворяют условию
, которые удовлетворяют условию 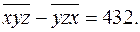
Решение. Отметим: так как 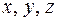 цифры числа, то
цифры числа, то
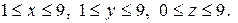
1. Имеем
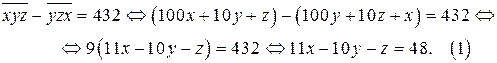
а) Рассмотрим уравнение (1) (выразим у через х и z)
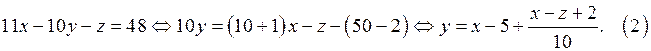 Так как
Так как 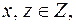 то у является целым числом, если существует число
то у является целым числом, если существует число 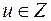 такое,
такое, 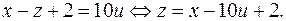
Из уравнения (2) находим, что 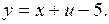
б) Оценим 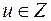 , если
, если 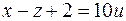
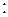
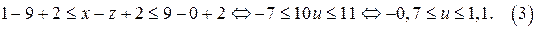
Так как 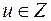 , то из двойного неравенства (3) следует, что
, то из двойного неравенства (3) следует, что 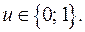
2. Найдём числа 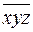 , если
, если 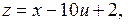
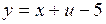 , где
, где 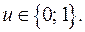
а) Если 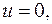 то
то 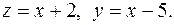 Оценим х.
Оценим х.
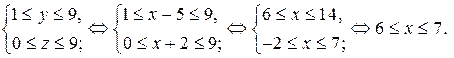
Так как 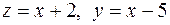 и
и 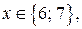 то
то 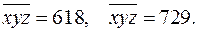
б) Если 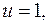 то
то  Оценим х.
Оценим х.
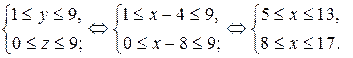
Так как 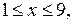 то из последней системы следует, что
то из последней системы следует, что 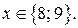
Так как 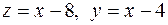 и
и 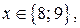 то
то 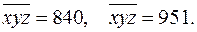
Ответ. 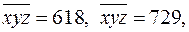
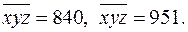
12. Найдите всевозможные трёхзначные числа, которые при делении на 27 даёт остаток, равный 4, при делении на 24 даёт остаток, равный 7, а при делении на 162 имеет одинаковый остаток.
Решение. 1. По условию задачи каждое искомое трёхзначное число х может быть представлено в виде 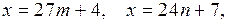 где
где 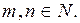
Тогда 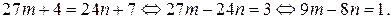
2. Найдём общее решение уравнения 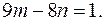
а) Преобразуем уравнение (выразим n через m)
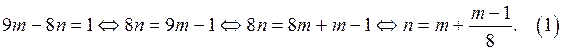
Так как 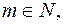 то
то 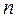 является целым числом, если существует число
является целым числом, если существует число 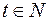 такое, что
такое, что 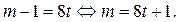
Отметим: так как надо найти число х, то 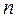 можно не находить.
можно не находить.
б) Если 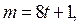 , то из (1) находим, что
, то из (1) находим, что 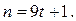
Таким образом, общим решением исходного уравнения является пара 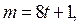
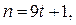 где
где 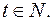
3. Найдём трёхзначные числа 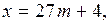 где
где 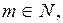 которые при делении на 162 имеет одинаковый остаток.
которые при делении на 162 имеет одинаковый остаток.
а) Так как 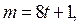 где
где 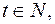 и
и 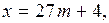 то
то
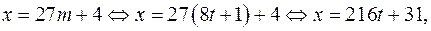 где
где 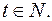
б) Оценим 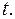
Так как 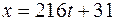 трёхзначное число и
трёхзначное число и 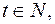 то
то
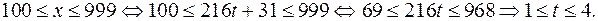
Так как 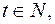 то
то 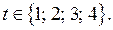
4. Найдём трёхзначные числа 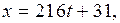 где
где 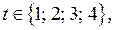 которые при делении на 162 имеет одинаковый остаток.
которые при делении на 162 имеет одинаковый остаток.
Если 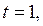 то
то 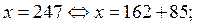
если 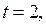 то
то 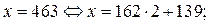
если 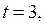 то
то 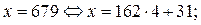
если 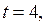 то
то 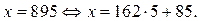
Числа 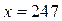 и
и 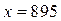 при делении на 162 имеют одинаковый остаток, равный 85.
при делении на 162 имеют одинаковый остаток, равный 85.
Ответ. 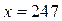 и
и 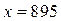 .
.
13. Найдите минимальное значение, на которое отличаются друг от друга натуральные числа 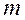 и
и 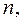 если дробь
если дробь 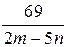 является простым числом.
является простым числом.
Решение. Так как 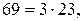 то исходная дробь является простым числом, если
то исходная дробь является простым числом, если
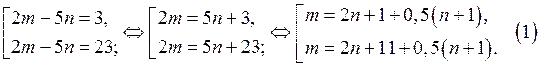
Так как 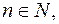 то т является натуральным числом, если существует число
то т является натуральным числом, если существует число 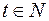 такое, что
такое, что 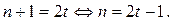
1) Если 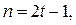 то из первого уравнения совокупности (1) находим, что
то из первого уравнения совокупности (1) находим, что 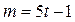 . Тогда общим решением уравнения
. Тогда общим решением уравнения 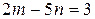 является пара
является пара 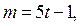
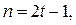 где
где 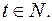
Если 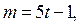
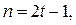 то
то 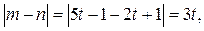 где
где 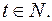 Так как
Так как 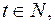 то
то 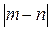 принимает минимальное значение, равное 3.
принимает минимальное значение, равное 3.
2) Если 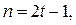 то из второго уравнения совокупности (1) находим, что
то из второго уравнения совокупности (1) находим, что 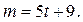 Тогда общим решением уравнения
Тогда общим решением уравнения 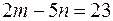 является пара
является пара 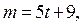
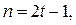 где
где 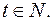 Если
Если 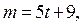
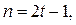 то
то 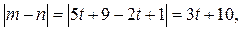 где
где 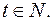
Так как 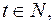 то
то 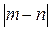 принимает минимальное значение, равное 13.
принимает минимальное значение, равное 13.
Из 1) и 2) следует: минимальное значение, на которое отличаются друг от друга натуральные числа 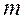 и
и 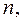 равно 3.
равно 3.
Ответ. 3.
Диофантов уравнения второго порядка
Диофантовым уравнением второго порядка с двумя неизвестными называется уравнение 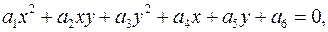 где
где
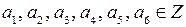 и хотя бы одно из чисел
и хотя бы одно из чисел 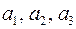 отлично от нуля.
отлично от нуля.
Упорядоченная пара 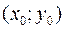 называется решением уравнения
называется решением уравнения 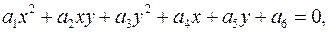 если
если 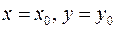 удовлетворяют уравнению.
удовлетворяют уравнению.
Решить уравнение в целых (натуральных) числах – это значит найти все целые (натуральные) решения или показать, что уравнение не имеет решений в целых числах.
1. Уравнения вида 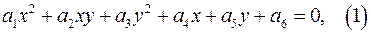 где
где
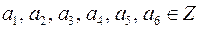 и хотя бы одно из чисел
и хотя бы одно из чисел 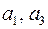 отлично от нуля.
отлично от нуля.
Для того, чтобы решить уравнение (1) в целых (натуральных) числах поступают следующим образом.
Уравнение (1) рассматриваем как квадратное относительно какой-нибудь переменной, например х, с параметром у.
Находим дискриминант 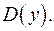
1. Если дискриминант 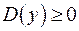 и является полным квадратом, то находим
и является полным квадратом, то находим 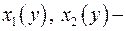 корни квадратного уравнения, а затем находим целые значения у, при которых
корни квадратного уравнения, а затем находим целые значения у, при которых 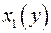 и
и 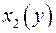 являются целыми числами.
являются целыми числами.
2. Если дискриминант 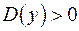 и
и 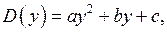 где
где 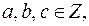 то возможны следующие случаи.
то возможны следующие случаи.
1) Пусть 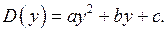 Если коэффициент при
Если коэффициент при 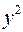 является полным квадратом, равным
является полным квадратом, равным 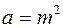 и коэффициент при
и коэффициент при 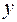 кратный 2 т, то записываем уравнение в виде
кратный 2 т, то записываем уравнение в виде 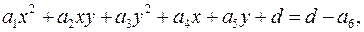
где 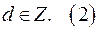
Рассматриваем многочлен 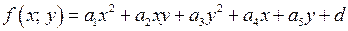 , где
, где 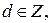 как квадратный трёхчлен относительно какой-нибудь переменной, например х, с параметром у.
как квадратный трёхчлен относительно какой-нибудь переменной, например х, с параметром у.
а) Находим дискриминант 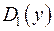 и выбираем d таким, чтобы
и выбираем d таким, чтобы 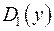 был полным квадратом.
был полным квадратом.
б) Находим 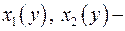 корни квадратного трёхчлена
корни квадратного трёхчлена 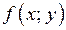 и
и
уравнение (2) принимает вид 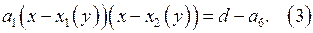
Замечание. Если 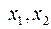 корни квадратного трехчлена
корни квадратного трехчлена
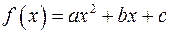 , где
, где 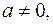 то
то 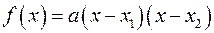 , где
, где 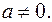
Так как надо решить уравнение (3) в целых (натуральных) числах, то 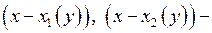 целые (натуральные) числа. Поэтому, представляем
целые (натуральные) числа. Поэтому, представляем 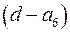 в виде
в виде 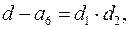 где
где 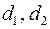 всевозможные целые (натуральные) числа. Для каждой пары
всевозможные целые (натуральные) числа. Для каждой пары 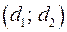 решаем в целых (натуральных) числах совокупность систем
решаем в целых (натуральных) числах совокупность систем
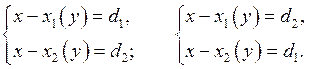
2) Пусть 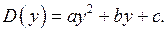 Если коэффициент при
Если коэффициент при 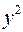 положительное число, решается одна из двух задач.
положительное число, решается одна из двух задач.
а) Доказать, что уравнение не имеет решение в целых (натуральных) числах. В этом случаи используется делимость целых чисел.
б) Доказать, что уравнение имеет решение в целых (натуральных) числах. Чтобы решить эту задачу, надо найти хотя бы одно решение в целых (натуральных) числах уравнения.
3) Пусть 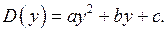 Если коэффициент при
Если коэффициент при 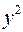 отрицательное число, то находим значения у, при которых
отрицательное число, то находим значения у, при которых 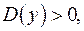 а затем перебором находим значения у, при которых
а затем перебором находим значения у, при которых 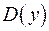 является полным квадратом.
является полным квадратом.
4) Пусть 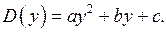 Если коэффициент при
Если коэффициент при 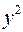 равен нулю, то для нахождения значения у, при которых дискриминант
равен нулю, то для нахождения значения у, при которых дискриминант 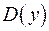 является полным квадратом, используется делимость целых чисел.
является полным квадратом, используется делимость целых чисел.
3. Если 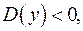 то уравнение не имеет решений.
то уравнение не имеет решений.
14. Найдите все целые решения уравнения
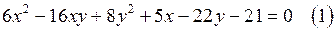
Решение. 1. Перепишем уравнение (1) как квадратное относительно х:
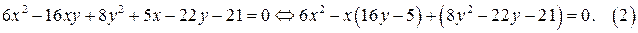 а) Найдём дискриминант
а) Найдём дискриминант 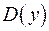 квадратного уравнения (2):
квадратного уравнения (2):
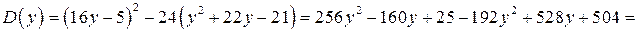
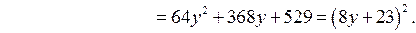
Итак, 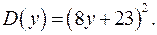
б) Найдём 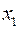 ,
, 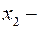 корни квадратного уравнения (2).
корни квадратного уравнения (2).
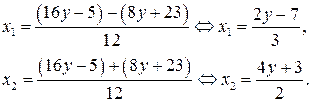
2. Найдём целые значения у, при которых 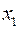 и
и 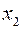 являются целыми числами.
являются целыми числами.
а) Число 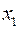 является целым числом, если
является целым числом, если 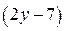 кратно 3.
кратно 3.
Преобразуем: 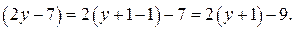
Если 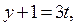 где
где 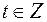 , то
, то 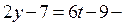 кратно 3.
кратно 3.
Итак, если 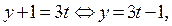 то
то 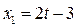 , где
, где 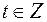 .
.
Таким образом, решением исходного уравнения является пара 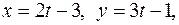 где
где 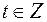 .
.
б) Число 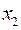 является целым числом, если
является целым числом, если 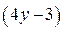 кратно 2. Так как
кратно 2. Так как 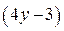 нечётное число, то оно ни при каких целых значениях у не будет кратным 2.
нечётное число, то оно ни при каких целых значениях у не будет кратным 2.
Ответ. 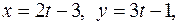 где
где 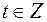 .
.
15. Найдите все целые решения уравнения
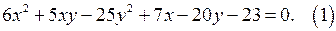
Решение. 1. Записываем уравнение (1) в виде:
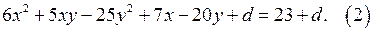
Рассматривается многочлен
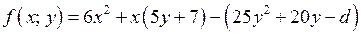 как квадратный трёхчлен
как квадратный трёхчлен
относительно х.
а) Найдём дискриминант 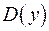 квадратного трёхчлена:
квадратного трёхчлена:
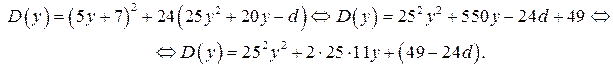
Очевидно, 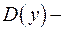 полный квадрат, если
полный квадрат, если 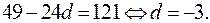
Таким образом, получили, если 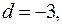 то
то 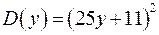 и
и 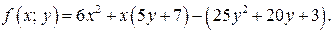
б) Найдём 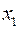 ,
, 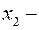 корни квадратного трёхчлена:
корни квадратного трёхчлена:
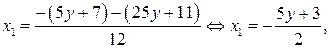
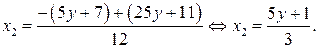
в) Найдём разложение квадратного трёхчлена на множители:
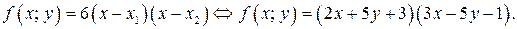
Так как 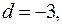 то при любых
то при любых 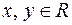 , уравнение (1) равносильно уравнению
, уравнение (1) равносильно уравнению 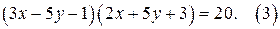
2. Так как 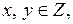 то
то 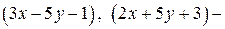 целые числа. Представляем число 20 в виде
целые числа. Представляем число 20 в виде 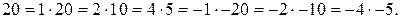
Для каждой пары 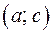 :
:
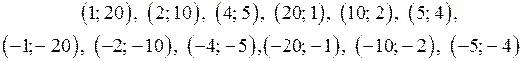
решаем в целых числах систему уравнений
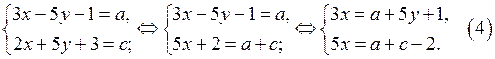
Система (4) может иметь решение в целых числах, если 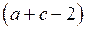 кратно 5. Легко проверить, что условие
кратно 5. Легко проверить, что условие 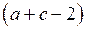 кратно 5 выполняется только для пар
кратно 5 выполняется только для пар 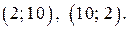
3. Найдём решение системы (4), если 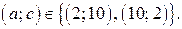
а) Если 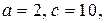 то
то 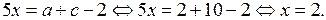
Из первого уравнения системы (4) находим, если 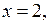 то
то 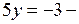 уравнение не имеет решений в целых числах.
уравнение не имеет решений в целых числах.
б) Если 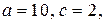 то
то 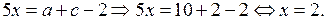
Из первого уравнения системы (4) находим, если 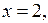 то
то 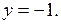
Так как 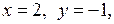 то решением системы (4), а значит и уравнения (1), является пара
то решением системы (4), а значит и уравнения (1), является пара 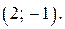
Ответ. 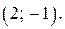
16. Докажите,что уравнение 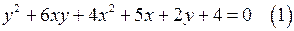 имеет решения в целых числах.
имеет решения в целых числах.
Решение. Чтобы решить эту задачу, надо найти хотя бы одно решение уравнения в целых числах.
1. Перепишем уравнение (1) как квадратное относительно у:
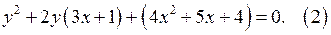
а) Найдём дискриминант 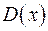 уравнения (2):
уравнения (2):
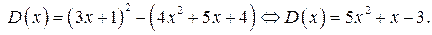
Представим, например, 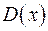 в виде
в виде 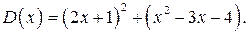
Очевидно, если 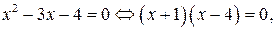 то
то 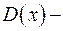 полный квадрат. Итак, если
полный квадрат. Итак, если 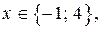 то
то 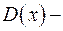 полный квадрат.
полный квадрат.
2. Найдём решение уравнения(1), если 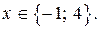
а) Если 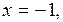 то уравнение (1) принимает вид
то уравнение (1) принимает вид

Итак, если 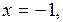 то
то 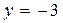 или
или 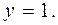 Тогда решениями уравнения (1) являются пары
Тогда решениями уравнения (1) являются пары 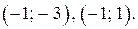
б) Если 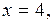 то уравнение (1) принимает вид
то уравнение (1) принимает вид
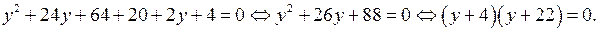
Итак, если 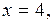 то
то 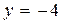 или
или 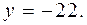 Тогда решениями уравнения (1) являются пары
Тогда решениями уравнения (1) являются пары 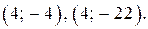
Уравнение (1) имеет решение в целых числах. Найдено четыре целых решения уравнения.
Отметим: Можно было найти только одно решение уравнения (1).
Ответ. Уравнение имеет решение в целых числах.
17. Решите уравнение 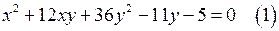 в целых числах.
в целых числах.
Решение. 1. Рассмотрим уравнение (1) как квадратное относительно х.
а) Найдём дискриминант 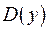 уравнения (1):
уравнения (1):
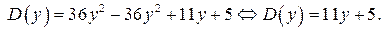
Уравнение (1) может иметь решение в целых числах, если 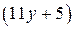 является полным квадратом. Число
является полным квадратом. Число 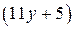 является полным квадратом, если существует число
является полным квадратом, если существует число 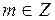 такое, что
такое, что 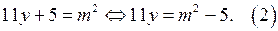 Уравнение (2) может иметь решение, если
Уравнение (2) может иметь решение, если 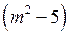 кратно 11.
кратно 11.
Пусть 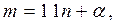 где
где
 2020-06-10
2020-06-10 2509
2509






