Формула гауссовой функции: причина ее возникновения, особенности.
Как же возникла эта кривая? В теории вероятностей гауссова кривая возникает при попытке практического использования формулы Бернулли. Теорема Бернулли дает абсолютно точный ответ для вероятности 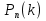 наступления
наступления 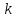 «успехов» в
«успехов» в 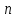 независимых повторениях одного и того же испытания с двумя исходами:
независимых повторениях одного и того же испытания с двумя исходами: 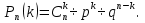
Но если мы будем вычислять по этой формуле, например,
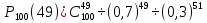 ,
,
то абсолютная точность не упростит, а усложнит нам задачу. Поэтому используются методы приближенного вычисления вероятностей. Оказывается, что в огромном числе различных ситуаций все приближения могут быть произведены с помощью одной-единственной функции – гауссовой функции 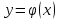 .
.
Доказал возможность такого использования функции 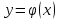 французский математик Пьер Симон Лаплас (1749-1827) - французский астроном, математик, физик, иностранный почетный член Петербургской АН, автор классических трудов по теории вероятностей и небесной механике, и, наконец, человек, который составил космогоническую гипотезу образования всех тел солнечной системы, называемую его именем и в общих чертах, неизмененную поныне.
французский математик Пьер Симон Лаплас (1749-1827) - французский астроном, математик, физик, иностранный почетный член Петербургской АН, автор классических трудов по теории вероятностей и небесной механике, и, наконец, человек, который составил космогоническую гипотезу образования всех тел солнечной системы, называемую его именем и в общих чертах, неизмененную поныне.
6. Таблица приближенных значений для гауссовой функции. Примеры.
Для использования столь громоздкой формулы гауссовой функции имеются подробные таблицы ее значений. Они составлены для значений аргумента с шагом 0,01.
выводится таблица.
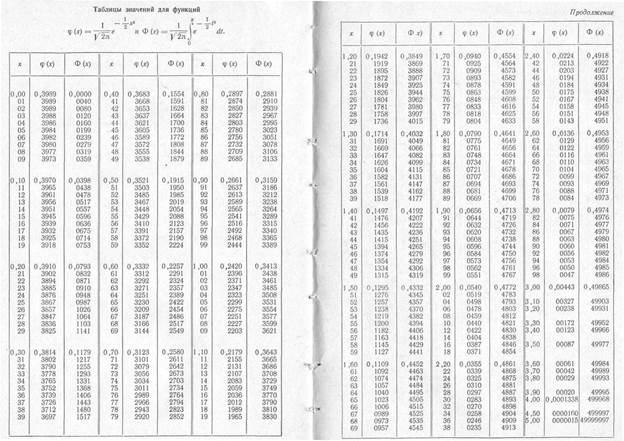
Рассмотрим способ использования гауссовой кривой для приближенных вычислений в теореме Бернулли.
Алгоритм использования функции Гаусса в приближенных вычислениях.
Алгоритм использования функции 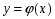 в приближенных вычислениях
в приближенных вычислениях
Для вычисления вероятности 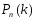 следует:
следует:
1. проверить справедливость неравенства npq 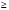 10;
10;
2. вычислить 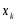 по формуле
по формуле 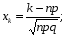
3. по таблице значений гауссовой функции вычислить 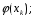
4. предыдущий результат разделить на 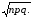
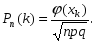
Рассмотрим внимательнее неравенство npq 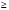 10. Так как
10. Так как 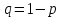 , то
, то 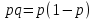 и наибольшее значение этого квадратичного выражения (относительно
и наибольшее значение этого квадратичного выражения (относительно 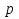 ) достигается при
) достигается при 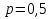 . Наибольшее значение равно 0,25. Значит,
. Наибольшее значение равно 0,25. Значит,
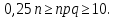
Поэтому из условия 1) алгоритма следует, что 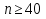 . Это значит, что указанный алгоритм дает хорошую точность приближения, когда испытание с двумя исходами независимо повторяется как минимум несколько десятков раз. При меньшем числе повторений точность приближения резко ухудшается.
. Это значит, что указанный алгоритм дает хорошую точность приближения, когда испытание с двумя исходами независимо повторяется как минимум несколько десятков раз. При меньшем числе повторений точность приближения резко ухудшается.
Задача.
Вероятность рождения мальчика примем равной 50%. Найти вероятность того, что среди 200 новорожденных будет 110 мальчиков.
Решение:
Будем действовать по предложенному алгоритму. В нашем случае п = 200, p = q = 0,5. Значит, npq = 50 > 10 и 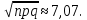 При этом число «успехов»
При этом число «успехов» 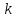 равно 110.
равно 110.
Тогда:
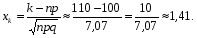
Используя таблицы, вычисляем ответ:
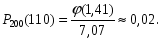
10. Алгоритм использования функции 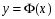 в приближенных вычислениях. Задача.
в приближенных вычислениях. Задача.
Алгоритм решения задач на нахождение 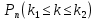 аналогичен уже рассмотренному для
аналогичен уже рассмотренному для 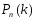 .
.
Алгоритм использования функции 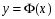 в приближенных вычислениях
в приближенных вычислениях
Для вычисления вероятности 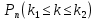 следует:
следует:
1. проверить справедливость неравенства npq 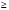 10;
10;
2. вычислить 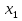 и
и 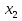 по формулам
по формулам
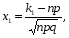
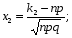
3. по таблице вычислить значения 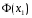 и
и 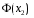
4. найти разность 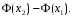
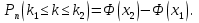
Задача.
Политика П. поддерживает в среднем 40% населения. Какова вероятность того, что из 1500 случайно опрошенных людей политика П. поддерживают от 570 до 630 человек?
Решение.
Считаем, что опрос 1500 человек происходит независимо и что вероятность поддержки политика П. отдельным респондентом, т. е. вероятность 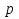 «успеха», равна 0,4. Тогда
«успеха», равна 0,4. Тогда
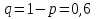 и
и 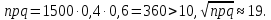
Значит, мы имеем дело с частным случаем схемы Бернулли, в которой число «успехов» 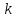 находится в пределах от 570 до 630.
находится в пределах от 570 до 630.
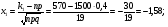
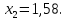
Поэтому 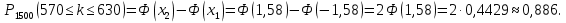
 2020-06-10
2020-06-10 1211
1211