Краткие теоретические сведения

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 16

Тема: Решение комбинаторных задач

Краткие теоретические сведения

Комбинаторика -раздел математики, посвящённый решению задач на выборку и перемещение конечных множеств относительно заданных правил.

В основе решения комбинаторных задач лежат 2 правила:

1) Правило суммы: если элемент a можно выбрать n способами, а элемент в – m способами, то а или в можно выбрать (n+m) способами.

2) Правило умножения: если элемент a можно выбрать n способами, а элемент в – m способами, то а и в можно выбрать (n*m) способами.

Определение: Любое упорядоченное множество, которое состоит из n -элементов, называется перестановкой из n-элементов.

Число всех перестановок из n -элементов выражают формулой:

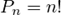
P_n-число перестановок из n-элементов.

Определение: Если из множества n элементов выбирают m в определенном порядке, это называется размещением.

(число размещений из n-элементов по m).

Определение: Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием.

 Число сочетаний из n элементов по m.

Задача 1. Сколькими способами можно расставить 5 книг на полке?

Решение: 5!=1*2*3*4*5=120 способов

Задача 2. Сколько двухзначных чисел можно составить из цифр 1,3,5,7,9, так чтобы в каждом числе не было одинаковых цифр?

Решение:

 способов

Задача 3. В классе 25 учеников нужно выбрать трех дежурных. Сколькими способами можно это сделать?

Решение.  способов

Задача 4. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать двух человек одного пола?

Решение: в данном случае подсчёт не годится, поскольку общее количество сочетаний включает в себя и разнополые пары.

Условие «выбрать двух человек одного пола» подразумевает, что необходимо выбрать двух юношей или двух девушек, и уже сама словесная формулировка указывает на верный путь решения:

способами можно выбрать 2 юношей;
способами можно выбрать 2 девушек.

Таким образом, двух человек одного пола (без разницы – юношей или девушек) можно выбрать: способами.

Содержание работы

Вариант 1.

Задача 1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?

Задача 2. Сколько трехзначных чисел можно составить из цифр 4,5,6,7,8,9 так, чтобы в каждом числе не было, одинаковых цифр?

Задача 3. Учащиеся группы БС-21 изучают 10 дисциплин. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различные дисциплины?

Задача 4. В вазе 8 красных и 3 белых розы. Сколькими способами можно выбрать из вазы 2 красных и 1 белую розы?

Задача 5. Сколькими способами в группе БС-21 можно из 23 человек отправить 5 человек участвовать в пробеге студентов колледжа?

Задача 6. В группе БС-21 14 девушек и 9 парней. Для дежурства в столовой требуется выделить 3 девушек и 2 парней. Сколько существует таких способов?

 

Вариант 2.

Задача 1. Номера машин состоят из 4 букв русского алфавита (33 буквы) и 3 цифр. Сколько существует различных номеров автомашин?

Задача 2. Сколько четырехзначных чисел можно составить из цифр 1,2,4,5,6,8,9 так, чтобы в каждом числе не было, одинаковых цифр?

Задача 3. Учащиеся группы БС-21 изучают 10 дисциплин. Сколькими способами можно составить расписание на один день, чтобы в нем было 5 различных дисциплин?

Задача 4. В урне 6 белых и 5 черных шаров. Сколькими способами можно вынуть из нее 2 белых и 3 черных шара?

Задача 5. Сколькими способами в группе БС-21 можно из 23 человек отправить 7 человек для участия в конкурсе «Веселые забавы»?

Задача 6. В группе БС-21 14 девушек и 9 парней. Для участия в спортивном мероприятии требуется выделить 4 девушек и 3 парней. Сколько существует таких способов?