Тема Параллельное включение приемников энергии

Цепь из двух параллельных ветвей (рис. а). Известны напряжение источника и параметры схемы. Нужно определить ток , потребляемый от источника, и угол сдвига на входе цепи. Для получения расчетных соотношений постройте векторную диаграмму токов, предварительно рассчитав токи в параллельных ветвях и углы их сдвига относительно приложенного напряжения. У первой ветви характер нагрузки индуктивный, ток отстает от на угол

………………………………………………………………………

У второй ветви характер нагрузки емкостный, вектор опережает на угол

…………………………………………………………………………….

В качестве основного вектора принимают вектор напряжения источника , являющегося общим для двух параллельных ветвей (рис. б). Тогда относительно него нетрудно сориентировать векторы токов .

Продолжите порядок построения векторной диаграммы

………………………………………………………………………………………

……………………………………………………………………………………….

…………………………………………………………………………………………..

…………………………………………………………………………………………...

Проекцию вектора тока на вектор напряжения назовем ………………….. тока , а перпендикулярную проекцию – ……………………………… . На диаграмме (рис. б) эти составляющие показаны для всех векторов. Составляющие токи и физически не существуют и должны рассматриваться только как расчетные. По диаграмме активная составляющая входного тока определяется как сумма активных составляющих токов в параллельных ветвях (представьте математическое выражение изложенного)

………………………….………………………………………………………………

…………………………..……………………………………………………………..

………………………………………………………………………………………..

где – активная проводимость цепи, равная арифметической сумме активных проводимостей отдельных ветвей

где – активная проводимость -й ветви.

Только в частном случае, когда ветвь представляет собой чисто активное сопротивление .

Реактивная составляющая входного тока определяется как алгебраическая сумма реактивных составляющих токов в параллельных ветвях. Реактивную составляющую ветви с катушкой считают положительной, а с конденсатором – отрицательной. Знаки учитывают при подстановке соответствующих значений (математическое выражение)

………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

где – реактивная составляющая проводимости цепи, равная алгебраической сумме реактивных проводимостей отдельных ветвей.

В общем случае

где – реактивная проводимость отдельной -й ветви,

Если рассматриваемая ветвь чисто реактивная: , проводимость является обратной реактивному сопротивлению. Ток на входе цепи

где – ……………………….. цепи, равная геометрической сумме …………………. и ………………. проводимостей.

Угол сдвига фаз также определяется из векторной диаграммы. На представленных ниже рисунках изображены векторные диаграммы. Присутствуют такие понятия, как входной ток , его составляющие и и напряжение источника . Определите, где располагается треугольник, образованный вектором тока и его проекциями , и , называемый треугольником токов …-……………………..

Если стороны этого треугольника разделить на напряжение 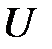, получится треугольник, подобный треугольнику токов – треугольник проводимостей-……………….

а) б) в)

Из треугольника проводимостей найдите соотношения между параметрами и формулы для определения угла сдвига фаз

………………………………………………………………………………………………..

Чтобы учесть знак 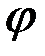, следует использовать формулы тангенса и синуса.

В этой цепи, когда общий ток совпадает по фазе с напряжением, а входная реактивная проводимость 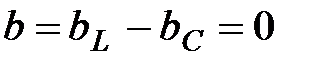или 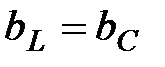, может возникнуть явление резонанса. При 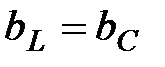противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в такой цепи получил название …………………………..