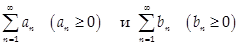Числовые ряды. Лекция 1
| I. Наводящие рассуждения |
1) Площадь квадрата. Рассмотрим квадрат со стороной 1 и будем разбивать его на части. При этом:
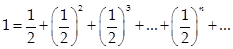
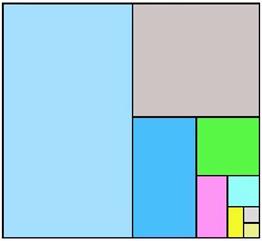
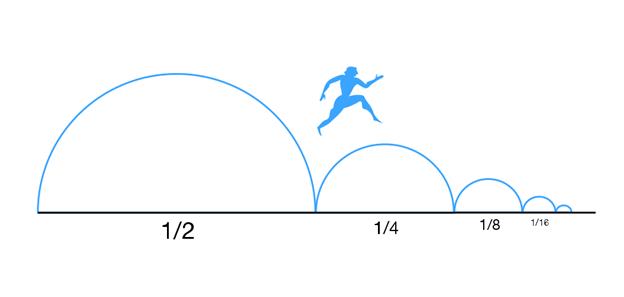
2) 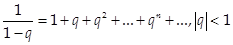
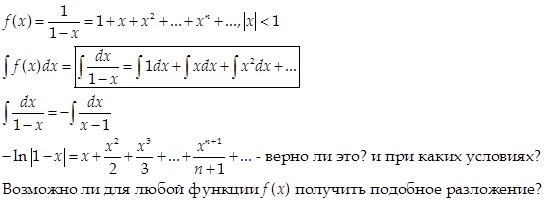
3)
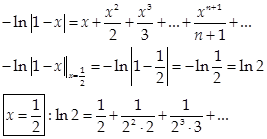
| II. Основные определения |
Определение Числовым рядом (рядом) называется выражение вида
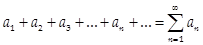 ,
,
при этом: 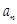 – общий член ряда;
– общий член ряда; 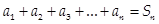 – частичная сумма ряда.
– частичная сумма ряда.
Если существует и конечен 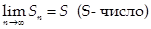 , то говорят, что ряд сходится и его сумма равна S, иначе – ряд расходится.
, то говорят, что ряд сходится и его сумма равна S, иначе – ряд расходится.
Таким образом, для того, чтобы выяснить, сходится ряд или расходится, нужно:
1) «Оборвать» его на n-ом слагаемом (т.е. получить частичную сумму Sn)
2) Вычислить предел 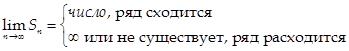
Примеры:
1)
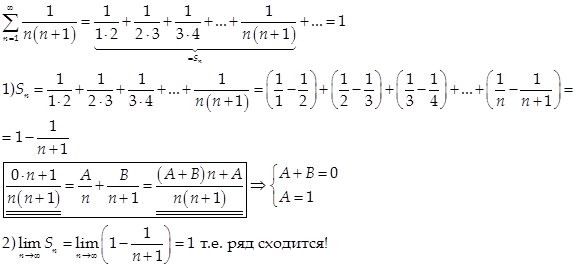
2)
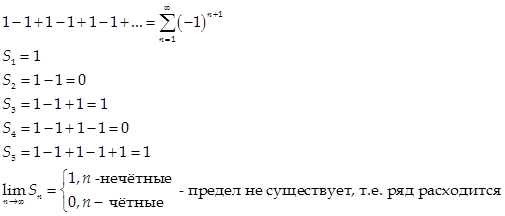
3)
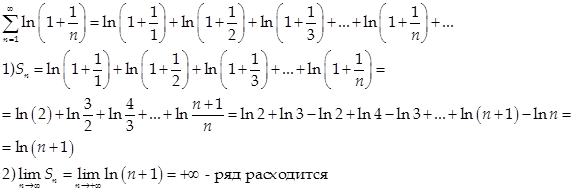
4) 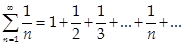
Необходимое условие сходимости ряда
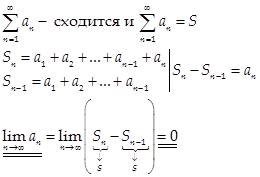
Если 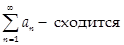 , то
, то 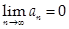
Если 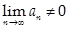 , то
, то 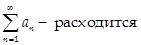
Примеры:
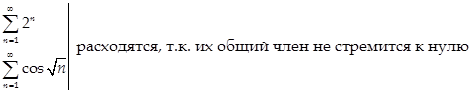
Обратное утверждение неверно! Т.е. существуют расходящиеся ряды, у которых 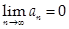 .
.
Пример: 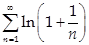 - расходится и при этом
- расходится и при этом 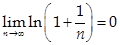
Свойства сходящихся рядов
1) Если 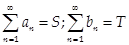 , то
, то 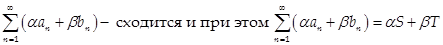 (при любых
(при любых 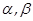 )
)
Если сгруппировать слагаемые в сходящемся ряде, то полученный ряд тоже будет сходится
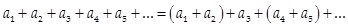
В общем случае от перестановки слагаемых сумма ряда может измениться
Пример:
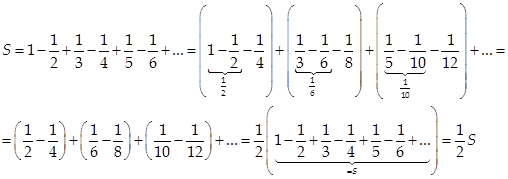
| III. Признаки сходимости рядов |
Ряды с неотрицательными членами
(1) Критерий сходимости ряда с неотрицательными членами:
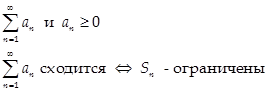
Доказательство:
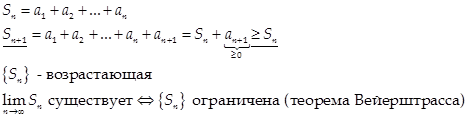
(2) Признаки сравнения
|
| |
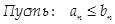 . Тогда:
(1) Если . Тогда:
(1) Если 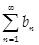 - сходится, то - сходится, то 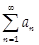 сходится;
(2) Если сходится;
(2) Если 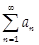 - расходится, то - расходится, то 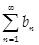 расходится расходится
| 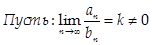 .
В этом случае ряды ведут себя одинаково (сходятся или расходятся одновременно) .
В этом случае ряды ведут себя одинаково (сходятся или расходятся одновременно)
|
Пример: 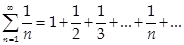 - расходится по признаку сравнения
- расходится по признаку сравнения
Пусть: 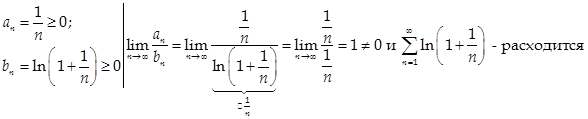
Замечание: Для сравнения удобно использовать обобщённый гармонический ряд
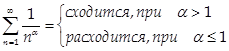
Или геометрический ряд
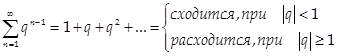
Когда удобно использовать признаки сравнения?
Когда общий член ряда — дробно-рациональное выражение.
Пример. 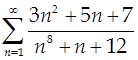 — сходится по признаку сравнения
— сходится по признаку сравнения
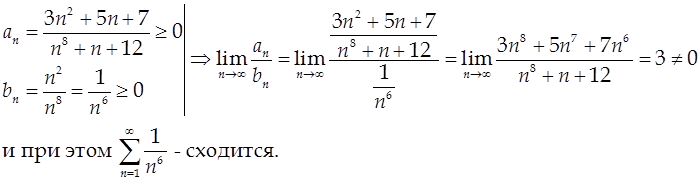
2) Если удаётся использовать эквивалентные величины.
Примеры. 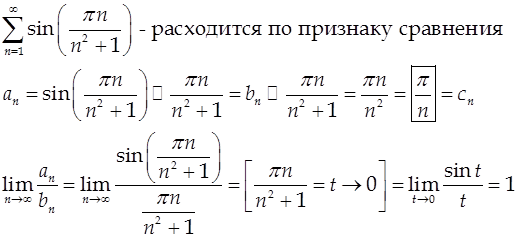
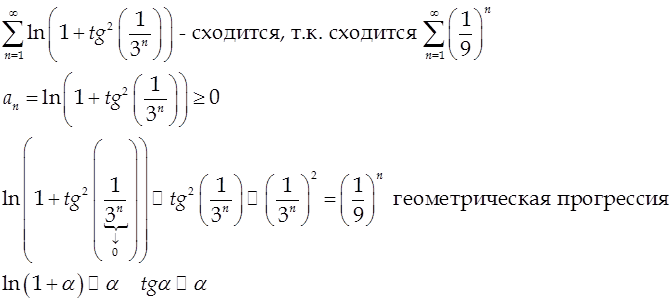
3) Наличие чётных степеней синуса или косинуса.
Пример.
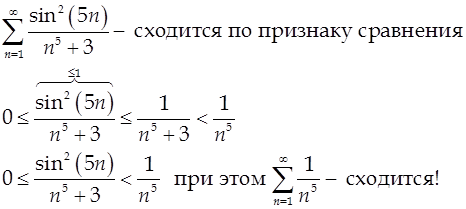
(3) Признак Д’Аламбера.
Пусть дан ряд 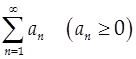 и и 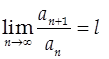
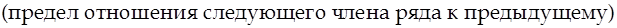 Тогда:
1) Если l <1, то ряд сходится
2) Если l> 1, то ряд расходится
3) Если l= 1, то ряд требует дополнительного исследования (признак ответа не даёт)
Тогда:
1) Если l <1, то ряд сходится
2) Если l> 1, то ряд расходится
3) Если l= 1, то ряд требует дополнительного исследования (признак ответа не даёт)
|
Признак Д’Аламбера удобно использовать в тех случаях, когда общий член ряда содержит степени и/или факториалы.
Примеры.
1.
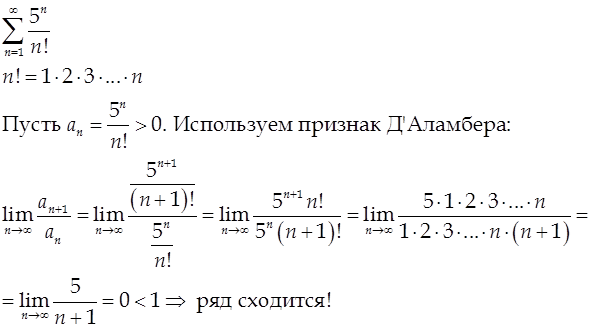
2. 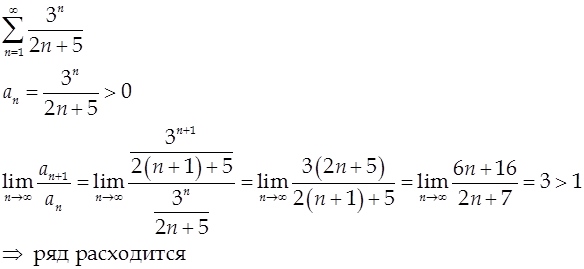
3. 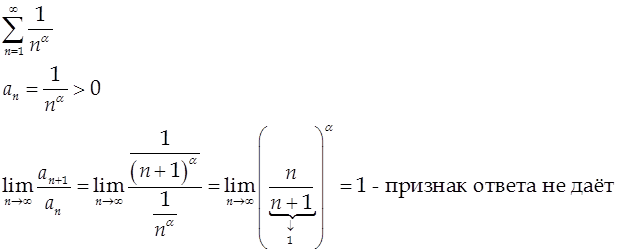
(4) Признак Коши (радикальный)
Пусть дан ряд 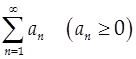 и и 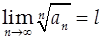
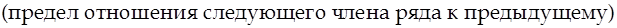 Тогда:
1) Если l <1, то ряд сходится
2) Если l> 1, то ряд расходится
3) Если l= 1, то ряд требует дополнительного исследования (признак ответа не даёт)
Тогда:
1) Если l <1, то ряд сходится
2) Если l> 1, то ряд расходится
3) Если l= 1, то ряд требует дополнительного исследования (признак ответа не даёт)
|
Признак Коши удобно использовать в тех случаях, когда общий член ряда содержит степени, показатели которых зависят от n.
Пример. 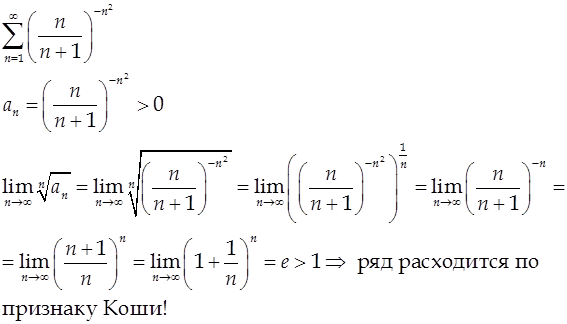
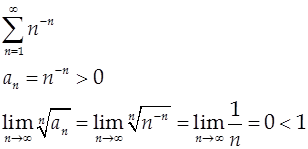
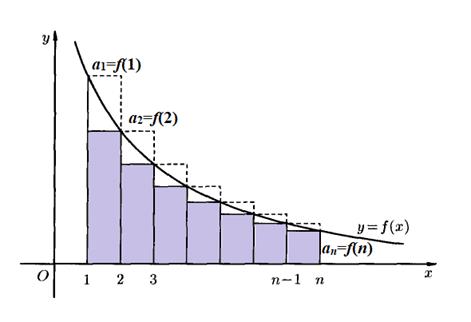
(5) Интегральный признак Коши
Пусть дан ряд 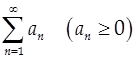 и на и на 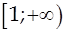 определена функция f(x) такая, что:
1) определена функция f(x) такая, что:
1) 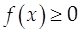 2)
2) 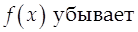 3)
3) 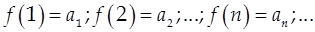 Тогда ряд
Тогда ряд 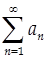 и несобственный интеграл и несобственный интеграл 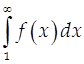 ведут себя одинаково (сходятся или расходятся одновременно) ведут себя одинаково (сходятся или расходятся одновременно)
|
Примеры.
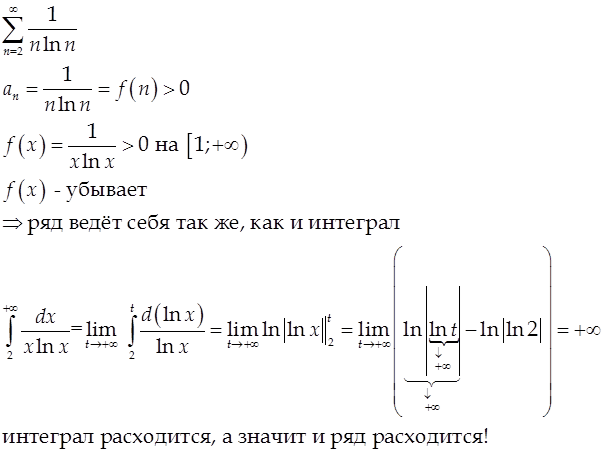
 2020-06-29
2020-06-29 81
81