Первый замечательный предел.
Теорема. Предел отношения sin бесконечно малой величины к самой этой величины к самой этой величине равен 1, т.е. 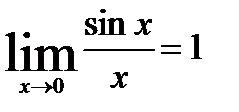 . Или
. Или 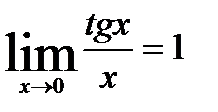
Теорема. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице, то есть 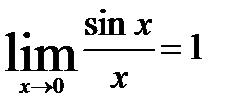 Этот предел называют первым замечательным пределом. С его помощью вычисляют пределы выражений, содержащих тригонометрические функции.
Пример 1. Вычислить
Этот предел называют первым замечательным пределом. С его помощью вычисляют пределы выражений, содержащих тригонометрические функции.
Пример 1. Вычислить 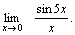 Решение. Преобразуем данное выражение:
Решение. Преобразуем данное выражение: 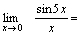 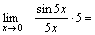 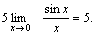 Пример 2. Найти
Пример 2. Найти 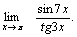 Решение. Для того чтобы воспользоваться первым замечательным пределом, перейдем к новой переменной
Решение. Для того чтобы воспользоваться первым замечательным пределом, перейдем к новой переменной 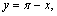 которая при которая при 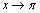 стремится к нулю. Тогда имеем стремится к нулю. Тогда имеем 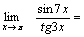 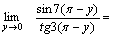 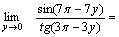 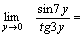 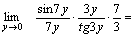 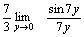 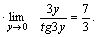 Второй замечательный предел:
Второй замечательный предел: 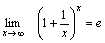 или или 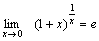 или или 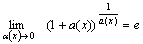 , , 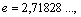 Пример 3. Найти
Пример 3. Найти 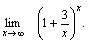 Решение. Полагая
Решение. Полагая 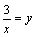 , получим: , получим: 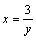 и и 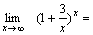 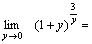 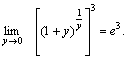 Пример 4. Найти
Пример 4. Найти 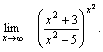 Решение. Преобразуем выражение, стоящее под знаком предельного перехода.
Решение. Преобразуем выражение, стоящее под знаком предельного перехода.
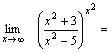 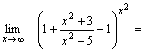 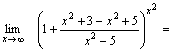 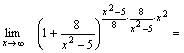 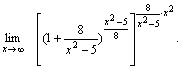 Так как
Так как 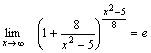 , а , а 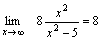 , то , то 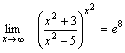 .
Для зачета по теме «Пределы», необходимо решить зачетную работу .
Для зачета по теме «Пределы», необходимо решить зачетную работу
|
Зачетная работа по теме «Пределы».
Вычислите пределы:
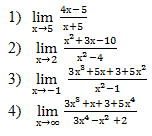 5)
5) 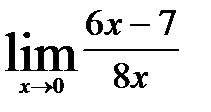 6) Найти предел функции:
6) Найти предел функции: 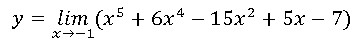
|
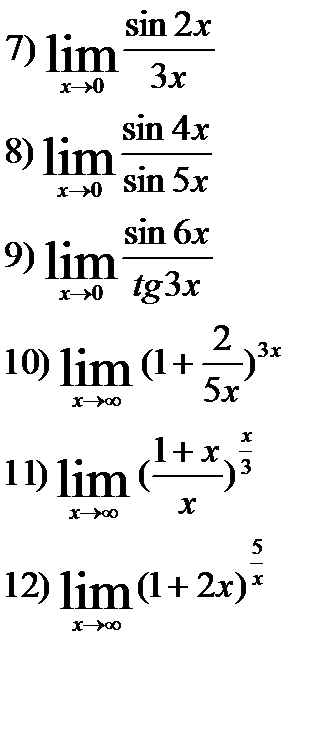
 2020-06-29
2020-06-29 191
191







