Практическая работа №18.
Тема: Построение графиков функций с помощью производной.
Цель: научиться строить графики функций, используя их исследование с помощью производной.
Теоретическая часть.
Общая схема исследования функции y=f(x).
- Найти область определения функции D(y);
- Определить чётность(нечётность) функции:
у=f(х) -чётная, если 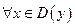 у(-х)=у(х)
у(-х)=у(х) 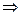 график функции симметричен относительно оси Оу;
график функции симметричен относительно оси Оу;
у=f(х) -нечётная, если 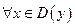 у(-х)=-у(х)
у(-х)=-у(х) 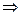 график функции и симметричен относительно начала координат О(0;0).
график функции и симметричен относительно начала координат О(0;0).
у=f(х) -ни чётная, ни нечётная, т.е. общего вида, если у(-х) 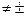 у(х)
у(х)
- Найти точки пересечения графика функций с осями координат:
а) с осью ОХ: 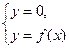
б) с осью ОУ: 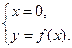
- Найти асимптоты графика функции:
а) вертикальные (находим среди точек разрыва)
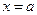 – вертикальная асимптота
– вертикальная асимптота 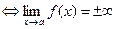
б) наклонные
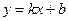 - наклонная асимптота
- наклонная асимптота 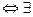
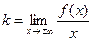 ;
; 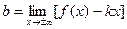
- Найти период функции, если
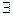 Т:
Т: 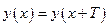
- Исследовать функцию на монотонность и экстремум:
а) найти 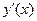 и критические точки
и критические точки 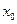 , т.е. точки из области определения функции, в которых
, т.е. точки из области определения функции, в которых  или терпит разрыв;
или терпит разрыв;
б) разбить область определения D(y) точками 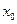 на интервалы и исследовать знак
на интервалы и исследовать знак 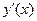 в каждом интервале;
в каждом интервале;
в) сделать вывод о монотонности:
если 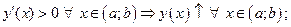
если 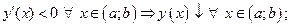
г) сделать вывод об точках экстремума;
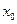 – точка max, если
– точка max, если 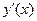 меняет знак с «+» на «–» при переходе через точку
меняет знак с «+» на «–» при переходе через точку 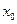
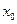 – точка min, если
– точка min, если 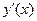 меняет знак с «–» на «+» при переходе через точку
меняет знак с «–» на «+» при переходе через точку 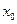
д) вычислить значение функции в точках экстремума, т.е. найти 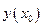 ;
;
е) составить таблицу:
| х | |
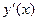
| |
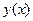
|
- Исследование функции на выпуклость и точки перегиба:
а) найти 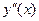 и критические точки
и критические точки 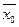 , т.е. точки из области определения функции, в которых
, т.е. точки из области определения функции, в которых 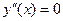 или терпит разрыв;
или терпит разрыв;
б) разбить область определения D(y) точками 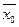 на интервалы и исследовать знак
на интервалы и исследовать знак 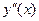 в каждом интервале;
в каждом интервале;
в) сделать вывод о выпуклости графика на каждом промежутке:
если 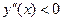 , то график обращён выпуклостью вверх
, то график обращён выпуклостью вверх  ;
;
если 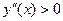 , то график обращён выпуклостью вниз
, то график обращён выпуклостью вниз 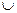 ;
;
г) определить точки перегиба:
если 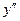 меняет знак при переходе через точку
меняет знак при переходе через точку 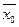 , то
, то 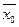 –точка перегиба
–точка перегиба 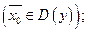
д) вычислить значение функции у в точках перегиба, т.е. найти 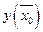 ;
;
е) составить таблицу:
| х | |
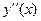
| |
|
- Построить график функции, вычислив, если необходимо, значения в дополнительных точках.
Практическая часть.
Пример 1. Исследовать функцию и построить её график 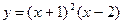
Решение.
1. D(y)=R.
2. Исследуем функцию на чётность и нечётность:
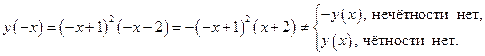
Таким образом, 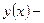 функция общего вида, симметрии у графика нет.
функция общего вида, симметрии у графика нет.
3. Точки пересечения с осями координат:
а) с осью ОХ: 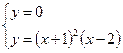 б) с осью ОУ:
б) с осью ОУ: 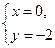 , т.е. С(0;-2).
, т.е. С(0;-2).
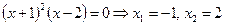 , т.е. А(-1;0), В(2;0)
, т.е. А(-1;0), В(2;0)
4. Асимптоты.
а) вертикальных асимптот нет, т.к. нет точек разрыва
б) наклонные асимптоты: 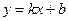
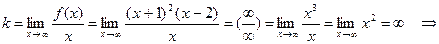 наклонных асимптот нет.
наклонных асимптот нет.
5. Периода нет, т.к. 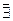 Т:
Т: 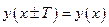 .
.
6. Промежутки монотонности.
Найдём 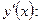
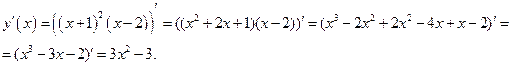
Найдём критические точки, т.е. точки, в которых 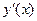 =0 или
=0 или 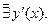

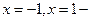 критические точки I рода.
критические точки I рода.
Составим и заполним таблицу:
| х | 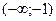
| -1 | 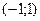
| 1 | 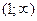
|
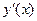
| + | 0 | - | 0 | + |
| 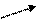
| 0 | 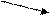
| -4 | 
|
max min
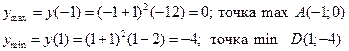
7. Промежутки выпуклости и вогнутости графика функций.
Найдём 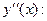
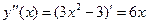 .
.
Найдём критические точки, т.е. точки, в которых 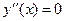 или
или 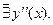
 6х=0 у
6х=0 у
|






 Составим и заполним таблицу:
Составим и заполним таблицу:
| х | 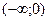
| 0 | 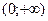
|
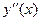
| - | 0 | + |
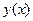
| 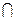
| -2 | 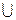
|

 | |||
 | |||



|
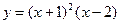
перегиб
у(0)=(0+1)2(0-2)=-2; точка перегиба С(0;-2)
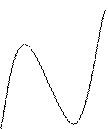
8. Построим график функции, вычислив значение в дополнительной точке х=-2:
| х | -2 |
| у | -4 |
Пример 2. Исследовать дробно-рациональную функцию и построить её график 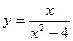
Решение:
1. 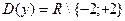
2. Исследуем функцию на четность и нечетность:
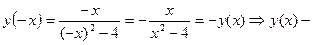 функция нечётная, и следовательно, график функции симметричен относительно точки О (0;0).
функция нечётная, и следовательно, график функции симметричен относительно точки О (0;0).
3. Точки пересечения с осями координат.
а) с осью ОХ: 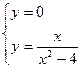
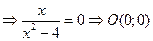
б) с осью ОУ: 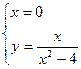
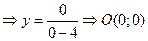
4. Асимптоты
а) вертикальные асимптоты:
х=2 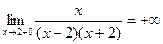 ;
; 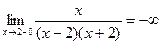
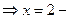 вертикальная асимптота
вертикальная асимптота
х=-2 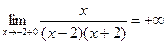 ;
; 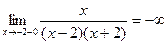
б) наклонные асимптоты: 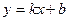
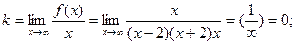
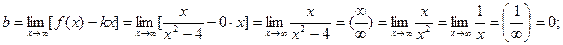
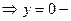 горизонтальная асимптота.
горизонтальная асимптота.
5. Периода у функции нет, т.к. 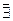 Т:
Т: 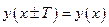 .
.
6. Промежутки монотонности.
Найдём 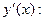
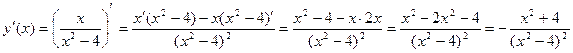
Т.к. 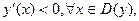 то функция убывает всюду в области определения.Точек экстремума у функции нет.
то функция убывает всюду в области определения.Точек экстремума у функции нет.
7. Промежутки выпуклости и вогнутости графика функции
Найдём 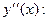
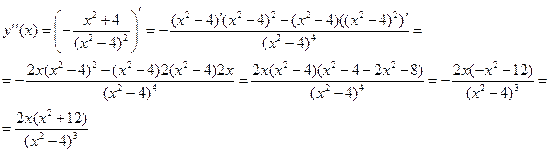
Найдём критические точки, т.е. точки, в которых 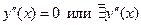
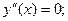
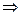
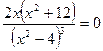 ;
; 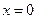
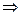
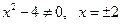
Итак, критические точки:
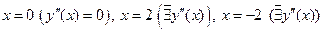 .
.
Составим и заполним таблицу, учитывая симметрию графика функции:
| х | 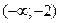
| -2 | 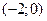
| 0 | (0;2) | 2 | (2;+ 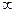 ) )
|
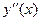
| - | 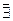
| + | 0 | - | 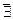
| + |
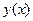
| 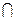
| 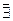
| 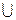
| 0 | 
| 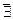
| 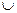
|
8. Построим график функции, вычислив значения в дополнительных точках:
| х | -3 | -1 | 1 | 3 |
| у | 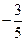
| 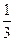
| – 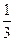
| 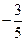
|
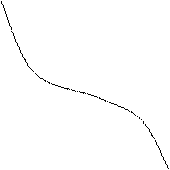

 у
у

Индивидуальные задания.
Исследовать функции и построить их графики.
Вариант №1
1. y=x2+2x-3;
2. y=x3+6x2+9x;
3. y=-2x- 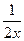 ; ;
| Вариант №2
1. y=4x2-6x-7;
2. y=x3-3x2-x+3;
3. y=3x+ 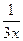 ; ;
| Вариант №3
1. y=3+4x-x2;
2. y=-x3+4x2-3;
3. y=x- 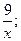
|
Вариант №4
1. y= 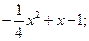 2. y=2+5x3-3x5;
3. y=
2. y=2+5x3-3x5;
3. y= 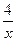 -x; -x;
| Вариант №5
1. y=-4x2+2x-1;
2. y=3x5-5x3;
3. 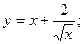
| Вариант №6
1. y= 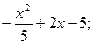 2. y=4x5-5x4;
3. y=x-
2. y=4x5-5x4;
3. y=x- 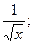
|
Вариант №7
1. y=x2+x-2;
2. y=3x5-10x3+15x;
3. y= 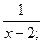
| Вариант №8
1. y=x2-2x+3;
2. y=x5-5x;
3. y= 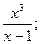
| Вариант №9
1. y=x2-6x;
2. y=-x3+4x-3;
3. y= 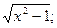
|
Вариант №10
1. y=3x-x2;
2. y=2+3x-x3;
3. y= 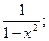
| Вариант №11
1. y=x2-10x+9;
2. y=x3-x2+x-1;
3. y= 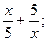
| Вариант №12
1. y=-x2+2x+3;
2. y=x5+x3+x-1;
3. y= 
|
Вариант №13
1. y=5x-4x2;
2. y=x3+3x2+3x
3. y= 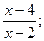
| Вариант №14
1. y=x2+2x+2;
2. y=1-2x+2x3-x5;
3. y=4+ 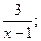
| Вариант №15
1. y=3x2-6x+3;
2. y=3-2x-2x2-x3;
3. y= 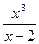
|
Вариант №16
1. y=-4x2+2x-1;
2. y=-x3+4x-3;
3. y=-2x- 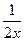 ; ;
| ||
 2020-06-30
2020-06-30 115
115






