Двадцать шестое мая
Классная работа
Повторение. Решение тригонометрических уравнений.
Порядок повторения темы: Решение тригонометрических уравнений.
1.Повторите формулы решения тригонометрических уравнений.(у вас есть таблица) или стр.171,177, 182 учебника.
2.Разберите и запишите в тетрадь решите уравнения: №656(4); №663(1), №674(2).
3. Пройдите тест:
1. Найдите все решения уравнения
2sinx-sin²x=cos²x.
1)  2)
2) 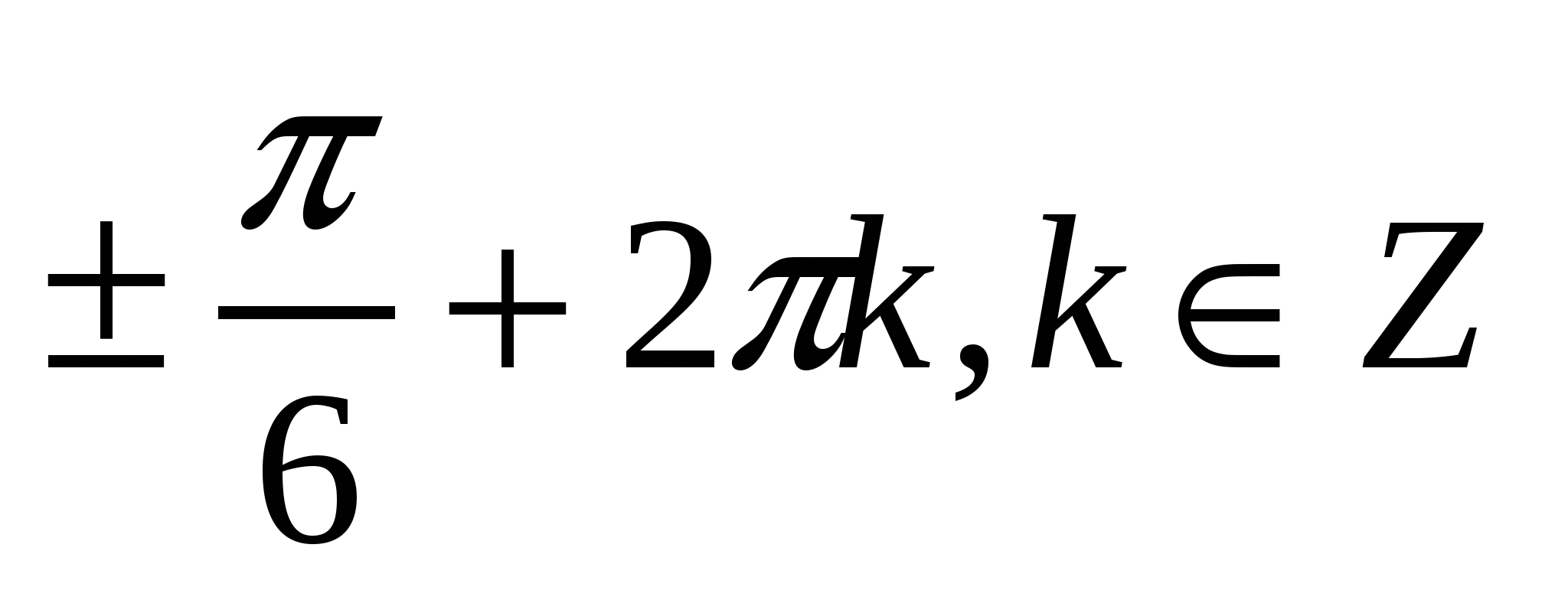
3)  4)
4) 
3.Решите уравнение  .
.
1)  2)
2) 
3) 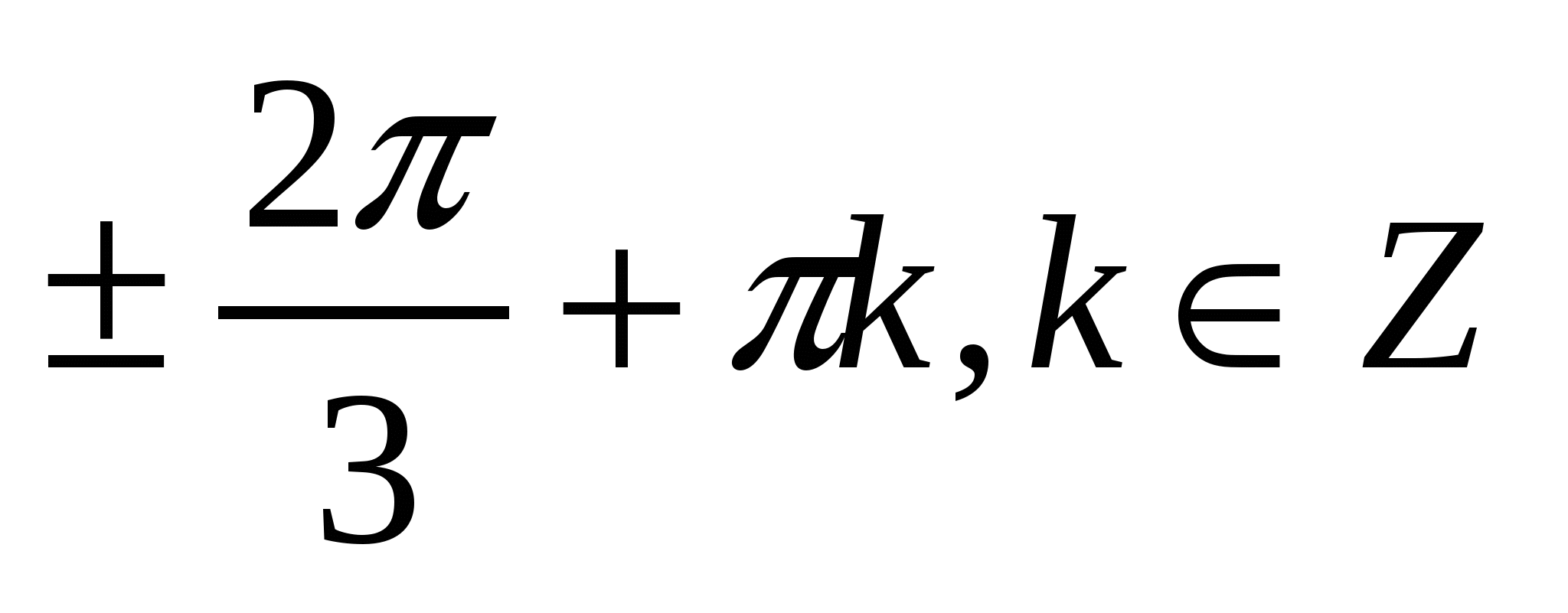 4)
4) 
4. Решите уравнение  .
.
1)  2)
2) 
3 ) π +6πn, n  Z 4) 2 πn, n
Z 4) 2 πn, n  Z
Z
4. Порядок повторения темы: Построение графиков функций.
| В школьном курсе математики изучаются следующие | ||||
| Название функции | Формула функции | График функции | Название графика | Комментарий |
| Линейная | y = kx | 
| Прямая | Cамый простой частный случай линейной зависимости - прямая пропорциональность у = kx, где k ≠ 0 - коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. |
| Линейная | y = kx + b | 
| Прямая | Общий случай линейной зависимости: коэффициенты k и b - любые действительные числа. Здесь k = 0.5, b = -1. Подробнее. К движению. |
| Квадратичная | y = x 2 | 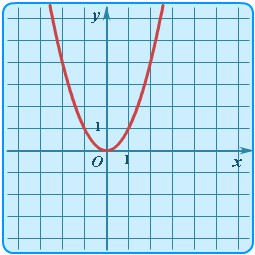
| Парабола | Простейший случай квадратичной зависимости - симметричная парабола с вершиной в начале координат. Демо упражнения. Видео на YouTube |
| Квадратичная | y = ax 2 + bx + c | 
| Парабола | Общий случай квадратичной зависимости: коэффициент a - произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c - любые действительные числа. Подробнее. К движению. |
| Степенная | y = x 3 | 
| Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе "Движение графиков функций". К движению. |
| Степенная | y = x 1/2 | 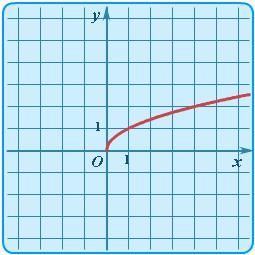
| График функции y = √ x | Самый простой случай для дробной степени (x 1/2 = √ x). Случаи с коэффициентами изучаются в разделе "Движение графиков функций". К движению √ x. К движению 3√ x. |
| Степенная | y = k/x | 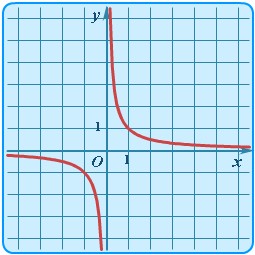
| Гипербола | Самый простой случай для целой отрицательной степени (1/x = x -1) - обратно-пропорциональная зависимость. Здесь k = 1. |
| Показательная | y = ex | 
| Экспонента | Экспоненциальной зависимостью называют показательную функцию для основания e - иррационального числа примерно равного 2,7182818284590... |
| Показательная | y = ax | 
| График показательной функции | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1). К движению. |
| Показательная | y = ax | 
| График показательной функции | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1). |
| Логарифмическая | y = ln x | 
| График логарифмической функции | График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой. |
| Логарифмическая | y = log ax | 
| График логарифмической функции | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2 x (a = 2 > 1). К движению. |
| Логарифмическая | y = log ax | 
| График логарифмической функции | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5 x (a = 1/2 < 1). |
2. Решите №125(1), №127 (1,2). №324 (1,3)
3.Просмотрите видео: https://www.youtube.com/watch?v=do8fqUQxWVc
https://www.youtube.com/watch?v=vCDdmEfQtdo
 2020-06-29
2020-06-29 116
116






