ПОВТОРЕНИЕ. Тема прошлого урока: Дифференциальные уравнения, в которых переменные уже разделены
Дифференциальные уравнения, в которых выражение, зависящее от y, входит только в левую часть, а выражение, зависящее от x - только в правую часть, это дифференциальные уравнения с разделенными переменными, в которых переменные уже разделены.
В левой части уравнения может находиться производная от игрека и в этом случае решением дифференциального уравнения будет функция игрек, выраженная через значение интеграла от правой части уравнения.
Пример такого уравнения 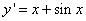 .
.
В левой части уравнения может быть и дифференциал функции от игрека и тогда для получения решения уравнения следует проинтегрировать обе части уравнения. Пример такого уравнения 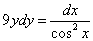 .
.
Пример 1. Найти общее решение дифференциального уравнения
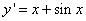
Решение. Пример очень простой. Непосредственно находим функцию по её производной, интегрируя:
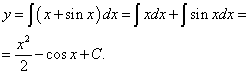
Таким образом, получили функцию - решение данного уравнения.
Пример 2. Найти общее решение дифференциального уравнения
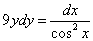
Решение. Интегрируем обе части уравнения:
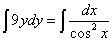 .
.
Оба интеграла - табличные. Идём к решению:
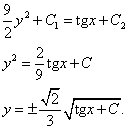
Функция - решение уравнения - получена. Как видим, нужно только уверенно знать табличные интегралы и неплохо расправляться с дробями и корнями.
ТЕМА Дифференциальные уравнения, в которых требуется разделить переменные
Дифференциальные уравнения с разделяющимися переменными, в которых требуется разделить переменные, имеют вид
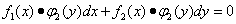 .
.
В таком уравнении 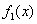 и
и 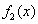 - функции только переменной x, а
- функции только переменной x, а 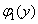 и
и 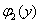 - функции только переменной y.
- функции только переменной y.

. 
ПРИМЕР 2 Найти общее решение дифференциального уравнения
. 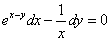
Решение.
Бывает, что забвение элементарной (школьной) математики мешает даже близко подойти к началу решения, задача выглядит абсолютно тупиковой. В нашем примере для начала всего-то нужно вспомнить свойства степеней.
Так как 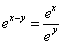 , то перепишем данное уравнение в виде
, то перепишем данное уравнение в виде
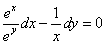 .
.
Это уже уравнение с разделяющимися переменными. Умножив его почленно на произведение 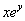 , получаем
, получаем
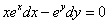 .
.
Почленно интегрируем:
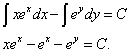
Первый интеграл находим интегрированием по частям, а второй - табличный. Следовательно,
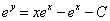 .
.
Логарифмируя обе части равенства, получаем общее решение уравнения:
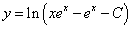 .
.
 2020-07-01
2020-07-01 72
72






