2020-07-01
880
Задача 1.
а) Привести квадратичную форму 
к каноническому виду методом Лагранжа, выписать преобразование координат.
б) Найти положительный и отрицательный индексы, ранг квадратичной формы 
в) Исследовать на знакоопределенность двумя способами: по каноническому виду и по критерию Сильвестра.
Решение:
a) Приведём к каноническому виду методом Лагранжа, то есть выделим полные квадраты:
= 
= 
где соответствующее преобразование координат имеет вид:
б) определим положительный 
и отрицательный 
индексы и ранг 
квадратичной формы по её каноническому виду
,
в) исследуем на знакоопределенность
-по каноническому виду: 
значит квадратичная форма знаконеопределена.
-по критерию Сильвестра: выпишем матрицу данной квадратичной формы
и вычислим главные миноры
квадратичная форма знаконеопределена.
Задача №2
При каком значении параметра 
квадратичная форма
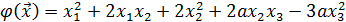
положительно определена?
Решение: Выпишем матрицу квадратичной формы:
и исследуем ее по критерию Сильвестра. Вычислим главные миноры:
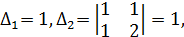
Согласно критерию Сильвестра, квадратичная форма положительно определена тогда и только тогда, когда все главные миноры положительны. В нашем случае минор
Ответ: квадратичная форма положительно определена при
Задача №3.
Исследовать тип поверхности, заданной уравнением
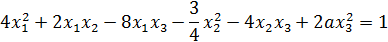
в зависимости от значения параметра 
Решение. Приведём квадратичную форму к каноническому виду методом Лагранжа
= 
Введём новые координаты
тогда уравнение поверхности второго порядка примет вид
Заметим, что канонический вид зависит от способа приведения квадратичной формы к такому виду. Но важным является факт, что остаются неизменными характеристики квадратичной формы, а именно ранг – количество квадратов в каноническом виде, положительный индекс – количество квадратов с плюсом, и отрицательный индекс – количество квадратов с минусом.
Продолжим исследование типа поверхности в зависимости от характеристик формы.
1) Если 
тогда
уравнение поверхности примет вид
и это уравнение задаёт в геометрическом пространстве двуполостный гиперболоид.
2) Если 
уравнение примет вид
и будет определять цилиндрическую поверхность (а именно гиперболическую)
3) Если 
тогда уравнение примет вид
и будет задавать в пространстве однополостный гиперболоид.
Задача полностью решена.
Задачи для самостоятельного решения:
1. В зависимости от значений параметра исследовать тип поверхности, заданной уравнением
2. Исследовать квадратичную форму на знакоопределённость в зависимости от значения параметра
3. Задача типового расчёта 2.12.
