Подготовительный этап

РАЗДЕЛ 12. УРАВНЕНИЯ И НЕРАВЕНСТВА

ТЕМА: Основные приемы решения уравнений

Цель занятия: научиться решать логарифмические уравнения.

Порядок выполнения работы:

1) Изучить теоритический материал, составить краткий конспект в тетради;

2) Выслать фотографии или документ преподавателю в социальной сети или на личную почту;

Контакты преподавателя: Arina_Kozlova96@mail.ru; https://vk.com/rina1996

ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ

Основные тождественные преобразования

· Замена одного выражения другим, тождественно равным ему.

Например, уравнение (3 x+ 2) ² = 15 x+ 10 можно заменить следующим равносильным: 

9 x ² + 12 x + 4 = 15 x + 10.

· Перенос членов уравнения из одной стороны в другую с обратными знаками.

Так, в предыдущем уравнении мы можем перенести все его члены из правой части в левую со знаком «–»: 9 x ² + 12 x + 4 – 15 x – 10 = 0, после чего получим:

 9 x ² – 3 x – 6 = 0.

· Умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля.

Уравнение x – 1 = 0 имеет единственный корень x = 1. Умножив обе его части на x – 3, мы получим уравнение (x – 1)(x – 3) = 0, у которого два корня: x = 1 и x = 3. Последнее значение не является корнем заданного уравнения x – 1 = 0. Это так называемый посторонний корень. И наоборот, деление может привести к потере корня. Так, если (x – 1)(x – 3) = 0 является исходным уравнением, то корень x = 3 будет потерян при делении обеих частей уравнения на x – 3.

· Возведение обеих частей уравнения в нечетную степень или извлечение из обеих частей уравнения корня нечетной степени. Необходимо помнить, что:

а) возведение в четную степень может привести к приобретению посторонних корней;

б) неправильное извлечение корня четной степени может привести к потере корней.

Уравнение 7 x = 35имеет единственный корень x =5. Возведя обе части этого уравнения в квадрат, получим уравнение: 49 x ²= 1225, имеющее два корня: x =5и x = – 5. Последнее значение является посторонним корнем.

Неправильное извлечение квадратного корня из обеих частей уравнения 49 x ²= 1225 даёт в результате 7 x = 35,и мы теряем корень x = – 5.

Правильное извлечение квадратного корня приводит к уравнению: | 7 x | = 35,следовательно, к двум случаям: 1) 7 x = 35,тогда x =5; 2) – 7 x = 35, тогда x = – 5. Следовательно, при правильном извлечении квадратного корня мы не теряем корней уравнения.

Решение уравнений

· Показательные уравнения.

 1) Если показательное уравнение сводится к виду a^x = a^b (1) где a > 0 и a ≠1, то оно имеет единственный корень х = b.

 2) Иногда, чтобы привести показательное уравнение к виду (1), необходимо в левой части уравнения вынести за скобки общий множитель а ^х, например:

 

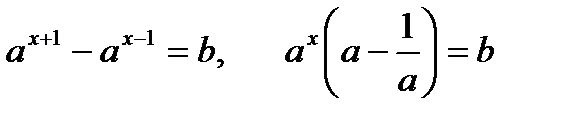
3) Некоторые показательные уравнения заменой а ^х = t сводятся к квадратным. 

Надо помнить, что t > 0, так как показательная функция не может принимать отрицательные значения.

· Логарифмические уравнения.

Чаще всего при решении логарифмического уравнения его приводят к виду

log _a (f(x)) = log _a (g(x)), тогда f(x) = g(x).

Решив полученное уравнение, следует сделать проверку  корней, чтобы исходное уравнение не потеряло смысл.

Подготовительный этап

Перепишите и заполните пропуски:

ПРИМЕР 1.  Решить уравнение: 9 ^х – 7 3 ^х = - 12

Решение:

 9 ^х – 7 3 ^х = - 12; Пусть 3 ^х = t, t > 0;   t² - 7t + 12=0; D = 1;  t₁ = 3, t ₂= 4.

Делаем обратную замену 1) 3^x = 3;                 2) 3^x = 4

x₁ =_____;                    x ₂ =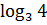                       

Ответ: х₁ = 1; x ₂ = .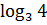

ПРИМЕР 2.  Решить уравнение: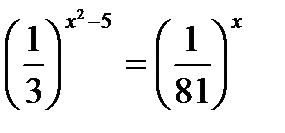  

Решение: 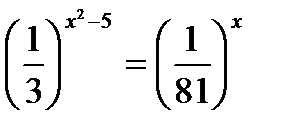    . Уравниваем основания: .

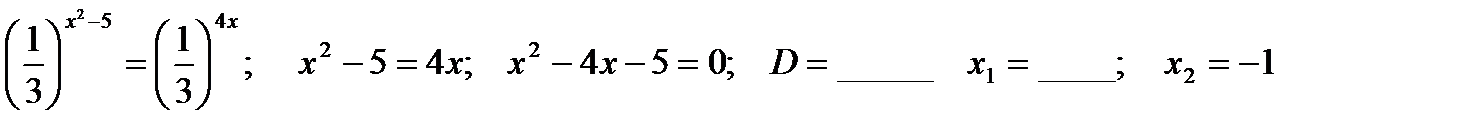Ответ: x₁= 5; x₂ = - 1

ПРИМЕР 3.  Решить уравнение:   log₅ (x² - 10) = log ₅ 9x

Решение: log₅ (x² - 10) = log ₅ 9x; x² - 9x – 10 = 0,

D =_____; x₁=10,  x₂= -1

Проверка: при х = 10, log₅ (10² - 10) = log ₅ (9 ∙10) – верно

Ответ: x = 10

ПРИМЕР 4.  Решить уравнение:  log ₇ (x² + 6x) = 1;

Решение: log ₇ (x² + 6x) = 1;

x² + 6x =7¹ ; x² + 6x – 7 = 0; D = 64; x₁ = - 7 u x₂ = _____

Проверка: при х = - 7, log ₇ ((- 7)² + 6 ∙(-7)) = 1 – верно

при х = 1, log ₇ (1² + 6 ∙1) = 1 – верно

Ответ. x₁= - 7; x ₂= 1.

ПРИМЕР 5.  Решить уравнение log₂ (x – 5) + log₂ (x +2) = 3

Решение: log₂ (x – 5) + log₂ (x +2) = 3

 Используем свойство логарифмов: log₂((x-5)(x + 2)) = 3;

(x-5)(x+2) = 2³;

(x-5)(x+2) = 8;  

 х² + …х – 5х – 10 = 8; x² – 3x - 18 = 0;  

D =_____; x₁ = – 3; x₂ =_____

Проверка: при x = – 3, log₂ (– 3 – 5) + log₂ (– 3 +2) = 3 – неверно

При х = 6, log₂ (6 – 5) + log₂ (6 + 2) = 3 – верно

Ответ:    х = 6.

Пример 6. Решить уравнение: .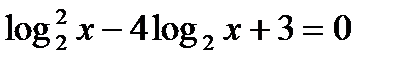

Решение: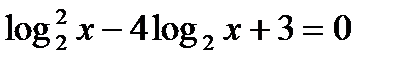

Пусть 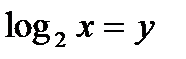, тогда у² – 4у + 3 = 0; D =____; у₁ = 1; у₂ =_____

Сделаем обратную подстановку:

1) 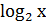 = 1; х = 2; 2)  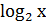= 3; х = 2³ ; х = ______

Ответ: х = 2, х = 8.